
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Цілочисельне лінійне програмуванняСодержание книги Поиск на нашем сайте
1-30. Знайти цілочисельне рішення задач. Дати геометричну інтерпретацію.
4.1 Пакет "The management scientist"
Пакет прикладних програм призначений для рішення задач з використанням методів математичного програмування і деяких задач, що містять статистичні залежності. Для початку роботи в пакеті потрібно запустити на виконання файл ms.exe. У діалоговому вікні, що з'явилося, пропонується вибрати диск, на якому буде відбуватися робота, на нього будуть записуватися збережені задачі і результати рішень. Припустимо, нами обраний диск С:, тоді як місце роботи вказують: С:. Головне меню програми має вигляд, представлений на мал. 1.
Малюнок 1 – Головне меню пакета
Вибравши необхідний пункт, вводять його номер, наприклад, 2 (це дозволить перейти до рішення транспортної задачі) і натискають клавішу ENTER. Для припинення роботи з пакетом треба ввести число 13 або натиснути разом клавіші CTRL і BREAK. Незалежно від обраного пункту з'являється стандартне “Меню вибору проблеми” (див. малюнок 2).
Малюнок 2 – Меню вибору проблеми
При записі математичної моделі діють наступні правила: § імена змінних повинні складатися не більш, ніж з 14 символів, індекси не використовуються, наприклад, XI, АВ12, З33; § дійсні числа вводяться з використанням точки, що відокремлює дробову і цілу частини 0.7; 3.61;
§ при програмуванні цільової функції першим указується її тип, а потім вводяться коефіцієнти при невідомих: max 10Х1+3Х2 чи min 7.4 XI + 6.8 X2; § запис виду.53 рівносильна 0.53. Якщо вводиться математична модель нової задачі чи викликається раніше створена, то наступний крок – це робота в меню, представленому на малюнку 3.
Малюнок 3 – Меню рішення задачі Для одержання рішення задачі вибирають опцію 1 (мал. 3), для збереження – 2. При збереженні модуля варто дотримуватись наступних правил: ім’я файлу не повинне перевищувати вісьмох знаків, причому забороняється використовувати пробіл, кому, “, /, [, ],:, <, >, +, =,;. Після того, як задача буде вирішена, з'являється меню, представлене на малюнку 4.
Малюнок 4 – Меню рішення проблеми Якщо необхідно скорегувати модель, у “Меню рішення задачі” (мал. 3) вибирається відповідний пункт, що передає управління “Меню редагування” (мал. 5).
Малюнок 5 – Меню редагування задачі Розглянемо приклад: Знайти максимум функції
У головному меню (мал. 1) виберемо опцію “Лінійне програмування”, потім, після переходу в меню вибору проблеми (мал. 2) задамо варіант “Створити нову проблему”. Впровадження моделі здійснюєтьсяпоетапно.
Крок I.
Крок II. Будь ласка, введіть обмеження:
Після появи слів “обмеження” ввестиумови, що накладаються, і натиснути ENTER. Коли всі умови будуть уведені,надрукувати END. обмеження 1: обмеження 2: обмеження 3: обмеження 4:
обмеження 5: обмеження 6:end Після завершення введення математичної постановки екстремальної задачі пакет автоматично переходить у меню роботи з проблемою (мал. 3). Перед подальшим використанням модель бажано зберегти, вибравши відповідну опцію меню. Дамо їй ім'я LP1. Рішення задачі буде роздруковане у вигляді Цільова функція Значення = 32.8
Величини, зазначені в стовпчику “Недолік/Надлишок”, означають резерв ресурсу, що присутній у відповідному обмеженні. Стовпчик “Відчутність” показує, на скільки покращиться оптимальне значення при збільшенні на одиницю значення правої сторони нерівності. Так, для другого обмеження підвищення ресурсу на одиницю приведе до збільшення значення цільової функції на 0.7. Аналогічно для інших обмежень.
Наступна таблиця характеризує: § нижні і верхні границі коефіцієнтів, у межах яких може мінятися один з коефіцієнтів, і при цьому рішення будуть забезпечувати ті ж значення змінних; § діапазони правої частини нерівностей, для якої відчутність залишається постійною.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 306; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.14.72.33 (0.01 с.) |


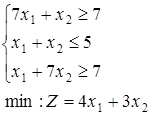

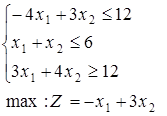
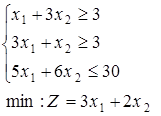
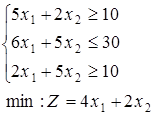




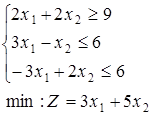



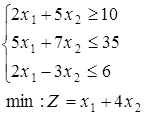



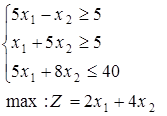





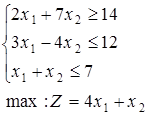





 при обмеженнях:
при обмеженнях:
 Введіть цільову функцію, використовуючи імена змінних з 14 символів або менше;
Введіть цільову функцію, використовуючи імена змінних з 14 символів або менше;

 < для менш чи дорівнює
< для менш чи дорівнює








