
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Графічний метод рішення задачСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте Лінійного програмування Даний метод застосовується для рішення задач, що містять не більш трьох змінних, найчастіше для задач із двома змінними. Він базується на наступних моментах: § множина припустимих рішень задачі опукла, у лінійному випадку вона являє собою кінцевий багатокутник, або багатокутник, що простирається в нескінченність; § цільова функція досягає свого оптимального значення у вершині області. Якщо вона приймає це значення в двох вершинах області, то оптимум досягається в будь-якій точці відрізка, що з’єднує ці вершини; § напрямний вектор (вектор нормалі) буде перпендикулярним до прямої функції цілі і завжди вказує напрямок її зростання. Схему застосування графічного методу проілюструємо на конкретному прикладі, розглядаючи три етапи: § побудова області припустимих рішень; § побудова напрямного вектора і визначення оптимальних точок; § знаходження оптимальних значень змінних і цільової функції.
Задача. Знайти максимальне і мінімальне значення функції
при обмеженнях
І етап. Побудова області припустимих рішень 1. Кожній нерівності ставимо у відповідність рівність, геометричним образом якої є пряма лінія. Для її побудови досить двох точок. §
§
§
§
2. Кожна пряма поділяє площину на дві півплощини, в одній з яких буде виконуватись відповідна нерівність. Щоб установити, точки якої півплощини будуть забезпечувати виконання нерівності, необхідно взяти довільну точку і її координати підставити в нерівність. Якщо для цієї точки нерівність виконалася, то рішенням нерівності буде та півплощина, у якій брали точку. Якщо нерівність для обраної точки не виконалася, то його рішенням будуть точки другої півплощини. Розглядаючи по черзі всі обмеження, одержимо область, у якій будуть справедливі всі нерівності, - це і є область припустимих рішень.
Нерівності ІІ етап. Визначення оптимальних точок. 1. Напрямний вектор проводять з початку координат у точку з координатами, що дорівнюють коефіцієнтам цільової функції, тобто в точку 2. Перпендикулярно напрямному вектору на області припустимих рішень проводять пряму 3. Якщо в задачі потрібно знайти максимум, то пряму 4. Якщо потрібно знайти мінімум, то пряму ІІІ етап. Визначення оптимальних точок. Щоб знайти змінні, що забезпечують екстремум, необхідно розв’язати систему рівнянь тих прямих, на перетинанні яких розташовується точка екстремума
Таким чином, знайдені максимальне і мінімальне значення функції, усі проміжні значення будуть досягатися в інших точках області припустимих значень. Зауваження 1. Якщо пряма функції Зауваження 2. Якщо область рішень не обмежена, то або задача не має рішення, або цільова функція може прийняти тільки максимальне чи тільки мінімальне значення, або задача має нескінченну безліч рішень. Симплексний метод
Симплексний метод є універсальним методом рішення задач лінійного програмування. Його алгоритм у тій чи іншій інтерпретації міститься практично у всіх підручниках і навчальних посібниках по цій дисципліні. Слід при цьому врахувати, що рішення потрібно починати з приведення задачі до канонічного виду. Рішення здійснюється в три етапи: а) будується початкове рішення; 6) проводиться оцінка знайденого рішення за відповідним критерієм оптимальності; в) якщо умова оптимальності не виконується, переходять до нового рішення. Етапи б) і в) виконуються доти, поки буде отримане оптимальне рішення. Усі правила проілюструємо на прикладі: Знайти
I етап. Побудова початкового рішення. а) Приводимо задачу до канонічного виду. 1. Необхідно перейти до визначення мінімуму, щоб усі правила розглянути для цього випадку. Якщо в умові потрібно знайти максимум, то переходять до мінімуму протилежної функції, а, вирішивши задачу, повертаються до заданої функції. У зазначеному прикладі:
2. Якщо серед вільних членів у системі обмежень є від’ємні, то відповідні обмеження множать на (–1). У нашому випадку це правило відноситься до ІІІ-го обмеження. У результаті його застосування система стане такою:
3. Якщо серед обмежень є нерівності, то, використовуючи додаткові змінні, перетворюють їх у рівняння. У нашому випадку:
Одержали канонічний вигляд задачі. б) В обмеження, де додаткові змінні віднімаються, додають штучні змінні з наступними номерами. Ці штучні невідомі вносять і в цільову функцію з коефіцієнтом
де
Усі змінні – невід’ємні. в) Виписують вектори коефіцієнтів при невідомих і вектор вільних членів.
г) будують першу симплексну таблицю наступного виду: Таблиця 1
Заповнюють таблицю за правилами: 1. Вносять усі вектори 2. У самий верхній рядок записують коефіцієнти цільової функції при відповідних змінних. 3. Первісний базис складуть вектори, що утворюють одиничну матрицю, - у даному випадку це вектори 4. У стовпець 5. Щоб одержати елементи двох останніх рядків, вектор
В д) Після того, як складена симплекс-таблиця, можна записати рішення. Воно завжди міститься в стовпці
ІІ етап. Перевірка оптимальності рішення а) Критерій оптимальності: функція досягає мінімуму, якщо серед елементів Додержуючись даного критерія, можемо укласти, що отримане з таблиці 1 рішення не є оптимальним: у б) У випадку, коли критерій оптимальності не виконується, вибирають ключовий стовпець – по найбільшому додатному числу в в) Визначають симплексні відносини, для цього елементи г) Ключовий рядок вибирають по найменшому симплексному відношенню (С.В.), він показує, який вектор вийде з базису. Найменше симплексне відношення дорівнює 1, ключовим буде другий рядок, з базису піде штучний вектор д) Елемент, що знаходиться на перетинанні ключового рядка і ключового стовпця, називається генеральним. У побудованій таблиці генеральний елемент дорівнює 5.
III етап. Побудова нового рішення (таблиці 2). а) Формують новий базис, заміняючи вектор б) Стовпець Таблиця 2
в) Обчислення ведуть за такими правилами. 1. Елементи ключового рядка поділяють на генеральний елемент і записують у нову таблицю. 2. Ключовий стовпець доповнюють нулями. 3. Якщо в ключовому рядку є нулі, то відповідні їм стовпці переносять без зміни – це 4. Інші елементи визначають за правилом прямокутника. Для його побудови в попередній таблиці старий елемент з’єднують із ключовим рядком і ключовим стовпцем, а потім по рядку і стовпцю ведуть до генерального елемента, (див. табл. 1)
Новий елемент знаходять так: обчислюють добуток елементів діагоналі, що містить генеральний елемент, з нього віднімають добуток елементів іншої діагоналі; одержану різницю поділяють на генеральний елемент, і результат вносять у нову таблицю (див. табл. 2). Наприклад, для стовпця
Для стовпця
Рішення, що відповідає Іі-й таблиці, беремо з
Для аналізу другого рішення повторюють усі дії, починаючи з II етапу. Перевірка показала, що в II таблиці умова оптимальності не виконується: є два додатних числа – це 9/5 і 1/5. Беруть найбільше і виділяють ключовий стовпець Таблиця 3
Рішення на базі таблиці 3 має вигляд:
Дане рішення не є оптимальним – перевірку ведемо по Таблиця 4
В
Дамо геометричну інтерпретацію симплексному рішенню. Для цього побудуємо область припустимих рішень і проаналізуємо, яким точкам відповідає кожна симплекс-таблиця. У розрахунок беремо тільки значення основних змінних
Область рішень не є кінцевою, а простирається в нескінченність і містить безліч точок, для яких виконуються всі обмеження. Першій симплекс-таблиці відповідають значення
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 620; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.33 (0.01 с.) |



 - ця пряма пройде через точки (2; 0) і (0; 3).
- ця пряма пройде через точки (2; 0) і (0; 3).

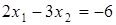 - ця пряма пройде через точки (-3; 0) і (0; 2).
- ця пряма пройде через точки (-3; 0) і (0; 2). - ця пряма пройде через точки (4; 0) і (0; -4).
- ця пряма пройде через точки (4; 0) і (0; -4). - ця пряма пройде через точки (7; 0) і (0; 4).
- ця пряма пройде через точки (7; 0) і (0; 4).
 й
й  означають, що область буде знаходитися в першій чверті. У нашому випадку областю припустимих рішень є точки п’ятикутника
означають, що область буде знаходитися в першій чверті. У нашому випадку областю припустимих рішень є точки п’ятикутника  .
.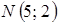 . Він завжди вказує напрямок зростання функції, напрямок спадання цільової функції буде протилежним.
. Він завжди вказує напрямок зростання функції, напрямок спадання цільової функції буде протилежним. (вона показана пунктиром).
(вона показана пунктиром). .
. .
.

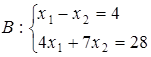



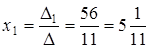






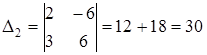


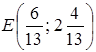

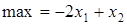 , при обмеженнях
, при обмеженнях



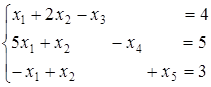


 . У результаті таких перетворень задача стає такою:
. У результаті таких перетворень задача стає такою: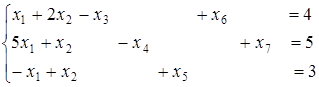
 ,
, – основні змінні;
– основні змінні; – додаткові змінні;
– додаткові змінні; – штучні змінні.
– штучні змінні.



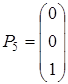




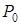
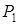
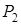
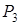
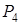



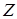 -строка
-строка
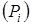 .
.

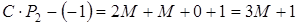




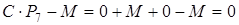
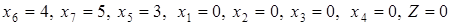 .
. .
.


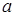

 – новий елемент,
– новий елемент, 
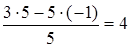


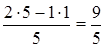

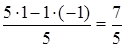

 .
. , знаходять симплексні відносини і вибирають ключовий рядок (перший), генеральний елемент дорівнює 9/5. Всі обчислення приводять до таблиці 3. З базису іде останній штучний вектор
, знаходять симплексні відносини і вибирають ключовий рядок (перший), генеральний елемент дорівнює 9/5. Всі обчислення приводять до таблиці 3. З базису іде останній штучний вектор 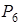 , тому таблиця 3 не буде містити стовпець
, тому таблиця 3 не буде містити стовпець  -рядок.
-рядок.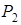
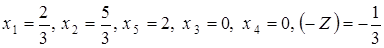 .
.
 .
.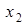 .
.
 , це точка
, це точка  – вона не лежить в області рішень, тому що в таблиці присутні штучні змінні. Другій таблиці відповідають
– вона не лежить в області рішень, тому що в таблиці присутні штучні змінні. Другій таблиці відповідають 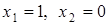 – це точка
– це точка  , вона теж знаходиться поза областю рішень. У третій таблиці штучні змінні виключені, тому рішення вже належить області рішень:
, вона теж знаходиться поза областю рішень. У третій таблиці штучні змінні виключені, тому рішення вже належить області рішень:  – це точка
– це точка  . Дана вершина не є оптимальною, ми переходимо до четвертої таблиці і до вершини
. Дана вершина не є оптимальною, ми переходимо до четвертої таблиці і до вершини  .
.


