
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Донецький державний університет економіки і торгівліСодержание книги Поиск на нашем сайте
Ім. М.Туган-Барановського
М а тем а тичне прогр а мув а ння Навчальний посібник для студентів спеціальностей “Облік і аудит”, “Банківська справа”, “Фінанси”
УДК 319.2
Математичне програмування. Навчальний посібник для студентів спеціальностей “Облік і аудит”, “Банківська справа”, “Фінанси” /Укладач Г.Г. Пеніна. – Донецьк, Дондует, 2004. – 107 стор.
Пропонується програма курсу, приведені методичні рекомендації з використання найважливіших методів рішення. Алгоритми рішення реалізовані на конкретних прикладах, які дозволяють опанувати основними принципами методів. Студенти повинні засвоїти, які задачі визначають дані напрямки, освоїти графічний і симплексний методи, розібратися з двоїстими задачами і матричними іграми, опанувати методом потенціалів, задачами про призначення, дробово-лінійним і параметричним програмуванням. Відповідно з тематикою дисципліни “Математичне програмування” наведені задачі для самостійного рішення.
Рецензенти: Сільченко В.О., канд.фіз.-мат наук, доцент Шепеленко О.В., канд.фіз.-мат наук, доцент
З м і с т
Вступ 1. Роль методів оптимізації в рішенні питань удосконалення керування економікою. 2. Місце математичного програмування в системі планування економіки. Приклади задач оптимізації. 3. Класифікація задач математичного програмування. Література: 1(стор. 4), 2(стор. 7), 3(гл. 1), 13.
I. Математичні основи програмування 1. Різні методи визначення лінійної залежності векторів. Поняття базису. Неєдиність базису. 2. Опуклі множини, основні теореми про них. 3. Системи лінійних рівнянь і нерівностей. Їхня геометрична інтерпретація. Література: 1(гл. 1), 2(гл. 2), 4(гл. 2), 5(гл. 1,5), 13. II. Загальний вигляд задачі лінійного програмування 1. Постановка задачі виробничого планування. 2. Математична модель транспортної задачі, необхідна і достатня умови можливості розв’язання. 3. Математична постановка задач про суміші, їхні відмінні риси. 4. Основна задача лінійного програмування, зведення до неї. Форми моделі, способи її перетворення. 5. Властивості рішення задачі лінійного програмування, його геометрична й економічна інтерпретації. Література: 1(гл. 1), 2(гл. 1,3), 4(гл. 3), 5(гл. 3), 12(гл. 2), 13
III. Методи рішення загальної задачі лінійного програмування 1. Графічний метод рішення, його характерні риси й обмеженість застосування. 2. Симплексний метод. Основна ідея методу, побудова вихідного опорного рішення. Критерій оптимальності задачі лінійного програмування. Перехід до поліпшеного рішення й алгоритм розрахунку. Схема застосування методу. 3. Метод штучного базису – модифікація симплексного методу. Зміни у формі задачі, алгоритмі рішення й інтерпретації змінних.
4. Алгебраїчний, економічний, геометричний зміст універсального методу рішення. 5. Випадки виродження задачі, зациклення та їх усунення. Монотонність і скінченність симплексного методу. Література: 1(гл.1), 2(гл.3), 4(гл. 4.6), 5(гл.4), 6(гл.2), 7(гл.2), 12(гл.4),13.
IV. Двоїсті задачі лінійного програмування 1. Структура, властивості і побудова симетричних задач. 2. Основні нерівності і теореми теорії двоїстості. Зв’язок рішень двоїстих задач. 3. Економічний зміст двоїстої задачі і її оптимального рішення. 4. Несиметричні двоїсті задачі й інтерпретація їхніх рішень. Література: 1(гл. 1), 4(гл. 5), 5(гл. 5), 6(гл. 2), 7(гл. 2), 12(гл. 5).
V. Розподільні методи 1. Характеристичні ознаки розподільних задач, їхній зв'язок із загальною задачею лінійного програмування. 2. Різні способи побудови вихідного опорного плану на прикладі транспортної задачі. 3. Критерій оптимальності плану транспортної задачі. Алгоритм рішення методом потенціалів. Метод диференціальних рент. 4. Задачі лінійного програмування, що приводяться до транспортної. 5. Задачі про призначення, особливості їх розв’язання. Література: 1(гл. 2), 2 (гл. 4), 4(гл. 10), 5 (гл. 6), 7 (гл. 3), 12(гл. 6). VІ. Елементи нелінійного програмування 1. Дробово-лінійне програмування, алгоритм їх зведення до загального вигляду. 2. Цілочисельне програмування. Економічні задачі, що зводяться до них. Поняття про методи рішення, геометрична інтерпретація цілочисельних задач. 3. Параметричне програмування. Економічні задачі, що зводяться до них. Алгоритм рішення параметричної задачі, що містить параметр у цільовій функції або в правій частині. Геометричний зміст рішення параметричної задачі. 4. Постановка загальної задачі нелінійного програмування Література: 1, 9, 10, 12 VII. Елементи теорії ігор 1. Економічні задачі, що приводять до ігрових моделей. Загальні поняття теорії ігор. Чисті, змішані, оптимальні стратегії. Сідлова точка. 2. Рішення ігор у змішаних стратегіях. Зв’язок матричних ігор із задачами лінійного програмування. Література: 3(гл. 13), 4(гл. 12).
Виниклі нові шляхи застосування математики викликали глибокі зміни в самій математичній науці. Вони не тільки викликали до життя нові значні напрямки теоретичної математики (з яких такі, як теорія ігор або теорія інформації, зайняли вже положення самостійних математичних наук), але і сприяли зміні сталих поглядів на раніше сформовані розділи. Найбільш істотним тут є те, що деякі розділи математики представляються нам тепер набагато більш змістовними і важливими, чим це здавалося математикам ХІХ століття і першої половини ХХ століття (як це відбулося, наприклад, з алгеброю). Якщо починаючи з XVII століття головне положення в математиці займало вивчення функцій неперервного аргументу, що є основою всіх застосувань математики у фізиці і техніці, то сьогодні можна говорити про відродження інтересу до “скінченої” математики. При цьому виникли нові підходи до цієї галузі математики, що йдуть в основному від математичної логіки. В даний час спостерігається “математизація” цілого ряду дисциплін, які раніше були далекі від усякого впливу математичних методів – лінгвістика, економічна теорія, медицина, педагогіка, психологія, теорія мистецтва.
Застосування математики в економічних дослідженнях дає можливість поглибити й уточнити уявлення про якісну сторону закономірностей, про істоту тих предметів і явищ, що піддаються дослідженню. Зупинимося на деяких, найбільш важливих напрямках економіко-математичних досліджень. 1. Використання математичних методів при встановленні економічно обґрунтованих цін, при розробці економічних критеріїв рентабельності, орієнтуючись на які окремі державні і приватні підприємства могли б повною мірою здійснювати господарський розрахунок і сполучити свої і державні інтереси. 2. Розробка міжгалузевих балансів виробництва і розподілу. У нас є деякий досвід балансових побудов. Однак поки ще не створена економіко-математична модель, що базувалася б на системі математичних рівнянь і нерівностей і давала можливість вирішувати різні економічні задачі. Побудова такої моделі забезпечить рішення екстремальних задач на мінімум витрат суспільної праці і на максимально можливий рівень матеріальної забезпеченості членів суспільства. 3. Забезпечення раціонального розміщення виробництва при плануванні роботи транспорту. До числа економічних проблем такого роду відноситься розподіл судів флоту між визначеними ділянками водяних шляхів, найкраще закріплення літаків за визначеними авіалініями, оптимальна експлуатація різних засобів транспорту при перевезенні різних видів вантажів, вибір раціональної схеми руху порожніх поїздів і т.д. 4. Рішення різноманітних техніко-економічних задач – задач на визначення оптимального плану використання виробничих потужностей (наприклад, завантаження верстатів), на раціональний розкрій матеріалів, на найвигідніше розташування господарських об’єктів (складів, магазинів і ін.), на оптимальний склад хімічних і інших промислових сумішів, на визначення найкращих харчових наборів і раціонів і т.ін. 5. Математика перестала бути допоміжною наукою, тепер вона – могутній апарат виробництва, профілююча дисципліна в економічних дослідженнях. Відзначимо особливу роль електронно-обчислювальної техніки при впровадженні математики в економіку. З появою комп’ютерних можливостей від математиків вимагають створення нових, більш могутніх обчислювальних методів, перед ними були поставлені нові обчислювальні задачі. Створення комп’ютерів і комп’ютерних технологій зробило революцію в області обчислювальної математики і привело до виникнення нового розділу сучасної математики – математичного програмування. До задач математичного програмування відносяться задачі оптимізації, що, як правило, не розв’язуються класичними прийомами. Це, насамперед, задачі математичної економіки. Вони виникають у тих випадках, коли дефіцитні ресурси – люди, машини, сировина – слід розподілити таким чином, щоб зробити необхідну кількість продуктів і щоб витрати при цьому були мінімальними (або доход максимальний). Величезний інтерес до цих задач пояснюється насамперед тим, що вони зустрічаються не тільки в теоретичній економіці, але й у практиці виробництва, торгівлі, управління й у військовій справі.
Точна економічна наука особливо потрібна тепер, коли неперервно розвивається економіка, і дуже ускладнилися господарські зв’язки. З математичної точки зору методи математичного програмування можуть бути застосовані лише до тих явищ і процесів, які виражаються позитивними величинами. Величини, що характеризують економічні явища, цим умовам, як правило, задовольняють. Математичне програмування можна застосовувати до таких задач, при рішенні яких оптимальний результат досягається лише у виді сформульованих цілей і при цілком визначених обмеженнях, що випливають із конкретних умов задачі. Отже, для будь-яких задач математичного програмування характерні три наступних моменти: ü наявність системи взаємозалежних факторів; ü строго визначений критерій оптимальності; ü точне формулювання умов, що обмежують використання наявних ресурсів і факторів. Рішення задачі досягається застосуванням певної математичної процедури, що полягає в послідовному наближенні раціональних варіантів, що відповідають обраним факторам, до оптимального плану. Зробимо кілька зауважень по постановці задач математичного програмування, вони торкаються ряду організаційних моментів. Математичний аналіз застосовується не до реальних явищ, а до деяких математичних моделей цих явищ. Такі абстрактні моделі, природно, охоплюють не всі, а лише найважливіші для даної задачі сторони явища. Найбільш кваліфікована і відповідальна робота при постановці задачі полягає у виборі характеристик явища – у рішенні, якими характеристиками зневажити і які врахувати. При виборі змінних бажано забезпечити можливо більш простий вид умов і критерію оптимальності. При побудові математичних моделей досліджуваних явищ, особливо в тих випадках, коли ці явища вивчаються вперше, не завжди удається відразу сформулювати і записати всі умови. Деякі фактори й обмеження, що представляються природними, передбачаються само собою зрозумілими і спеціально не обмовляються. Так, відомі, наприклад, випадки, коли при рішенні задачі про дієту з мінімальною вартістю не були враховані смакові характеристики дієти. У результаті були отримані зовсім не їстівні раціони. Іноді зустрічаються випадки, коли рішення, яке є оптимальним з формально-математичних позицій, недопустимий для виробництва як не задовольняючій економічним, технологічним і іншім вимогам, що запропоновані для даного виробничого процесу.
Отже, застосування методів математичного програмування може принести користь тоді, коли умови задачі враховують економічні, технологічні й інші особливості процесу. Тому постановку серйозних задач математичного програмування доцільно проводити фахівцям прикладних наук разом з математиками. Одним з найважливіших розділів сучасної математики є теорія ігор. Вона займається вивченням конфліктних ситуацій. Теорія ігор викликана до життя практичними потребами в моделях і методах економічного і військового планування. Ця теорія розвивалася незалежно від математичного програмування, поки в 50-х роках не був виявлений чудовий зв'язок між лінійним програмуванням і теорією ігор. Переплетення і взаємне проникнення цих дисциплін виявилися корисними для кожної з них. Обчислювальні прийоми лінійного програмування збагатилися методами рішення ігор (ітеративними) і навпаки. Класифікація задач математичного програмування. Задачі і методи математичного програмування можна класифікувати, виходячи з різних ознак. Корисно знати хоча б одну з існуючих класифікацій, що, насамперед, виявляє в задачі наявність елемента випадковості чи його відсутність. Задачі математичного програмування можуть бути розділені на два великих класи: детерміновані задачі і стохастичні (імовірнісні). Детермінованими називаються такі задачі, у яких критерій оптимальності не є випадковою функцією параметрів. У таких задачах з високою вірогідністю можна визначити необхідні умови здійснення дій (обмеження) і результати цих дій. Параметри в цих задачах також не є випадковими величинами. Стохастичними називаються задачі, що містять у собі невизначеність. Критерій оптимальності в таких задачах є деякою характеристикою випадкової функції параметрів задачі. Невизначеність може виникнути в багатьох випадках. Результати деякої дії можуть залежати від таких факторів як погода, затримка автотранспорту, рівень зайнятості, підвищення чи падіння купівельного попиту. Клас детермінованих задач підрозділяється на лінійні задачі і нелінійні. Стохастичні задачі можна теж розбити на дві групи, кожна з яких у свою чергу підрозділяється на підгрупи. У тих випадках, коли цільова функція (чи критерій оптимальності) виражена лінійно через вихідні фактори, а умови, що обмежують використання наявних ресурсів чи факторів, записуються у виді лінійних нерівностей або рівностей щодо змінних, ми приходимо до задачі лінійного програмування. Варто помітити, що в рамки лінійного програмування укладається величезна кількість найрізноманітніших задач перспективного й оперативного планування господарства, управління різного роду процесами. Майже паралельно з лінійним програмуванням розвивається нелінійне, що представляє більш складну математичну задачу. В даний час ще не можна говорити про закінчену теорію нелінійного програмування, але розробка її здійснюється дуже інтенсивно. З нелінійних задач виділяються задачі опуклого програмування. До задач опуклого програмування відносяться задачі, у яких показники якості й область визначення функції передбачаються опуклими. Між лінійним і опуклим програмуванням існує тісний зв’язок. Будь-яка опукла задача може бути зведена до задачі лінійного програмування. Серед задач опуклого програмування більш за все досліджені задачі квадратичного програмування. Для них характерно те, що функції цілі являють собою квадратичну форму, а обмеження лінійні. Вже зараз є методи для рішення задач квадратичного програмування і більш загального типу. Сучасна математична наука має у своєму розпорядженні цілий арсенал методів, що дозволяють вирішити задачу оптимального управління. Серед них особливе місце займає метод динамічного програмування. Специфіка цього методу полягає в тому, що для знаходження цього оптимального управління операції розділяються на ряд послідовних “кроків” чи “етапів”. Відповідно і сам процес планування стає “багатокроковим” і розвивається послідовно від етапу до етапу, причому щораз доводиться оптимізувати управління тільки на одному етапі. Якщо ми розглядаємо економіко-математичну модель не як застиглу задачу, а беремо її в динаміці, бажаючи знайти рішення на кілька періодів часу, то, природно, виникає динамічна задача, і має сенс говорити про динамічне програмування. Динамічні моделі найбільш цікаві для планових розрахунків, якщо планову економіку розглядати з точки зору управлінських систем, а також при рішенні задач розкрою та ін. задач. Дослідження задач, у яких коефіцієнти обмежень, коефіцієнти лінійної форми, а також праві частини обмежень залежать від параметра, складає предмет параметричного програмування. У цій області ще багато невирішених проблем. Розглянутий детально лише окремий випадок, коли від параметра залежать коефіцієнти лінійної форми або правої частини обмежень. Цілочисельними прийнято називати такі задачі лінійного програмування, у яких змінні повинні приймати лише цілі невід’ємні значення з припустимої області. Подібні задачі можуть виникнути різними шляхами. Насамперед, існують задачі, що формально не відносяться до цілочисельних, але їх рішення при цілих вихідних даних автоматично виходять цілочисельними. Це, наприклад, відома транспортна задача і її різні варіанти. Найбільш природним джерелом цілочисельних задач є найважливіші в прикладному відношенні задачі лінійного програмування, у яких потрібно скласти план використання неподільних ресурсів (наприклад, холодильників). Цілочисельне програмування здобуває особливий інтерес, тому що багато нелінійних опуклих задач математичного програмування можуть бути зведені до задач лінійного програмування з додатковою вимогою цілочисельного рішення. Ми вже відзначали, що задачі, у яких не можна зневажити помилками експерименту, називаються стохастичними. Це означає, що в такій задачі коефіцієнти цільової функції і системи обмежень не можна установити однозначно. А це приводить до того, що зі зміною одного чи кількох коефіцієнтів змінюються оптимальні рішення. Стандартні методи дають оптимальне рішення тільки для визначеного набору значень параметрів, тому їх використання утруднюється. Якщо для випадкових величин, що фігурують у задачі, відомо ймовірносний розподіл, то задача вирішується в умовах ризику. Якщо ймовірносний розподіл невідомий, то маємо задачу в умовах невизначеності. Прикладом задач в умовах ризику є задачі управління запасами, а задачі спеціального стохастичного аналізу можуть опинитися в умовах невизначеності. З усіх розділів математичного програмування стохастичне найменш розроблене.
2.1 Приклади задач лінійного програмування Промислове виробництво, ресурси в економіці, напруга сил у воєнних діях – це комплекси численних взаємопов'язаних процесів. У керуванні цими зовсім різними явищами можна виділити істотні риси подібності. При формулюванні задач оптимізації виявляється, що задачі, різні за змістом, можуть бути представлені однотипними математичними моделями. Найбільш простою і вивченою є модель лінійного програмування. Вона містить у собі три основних моменти: § набір невід’ємних змінних, що характеризують досліджуваний процес чи явище; § співвідношення, що встановлюють зв’язок між змінними (обмеження) і вимоги задачі, що відбивають; § критерій оптимальності (функцію цілі). У задачах лінійного програмування обмеження являють собою систему лінійних нерівностей і рівнянь, що виражають умову матеріального балансу (тобто щоб витрата будь-якого виду сировини не перевищувала наявний запас даної сировини і т.д.). Функція цілі теж має лінійний вид. Перш ніж перейти до розгляду загальної задачі лінійного програмування, розберемо кілька прикладів.
Задача виробничого планування. Припустимо, що на деякому підприємстві мається Задача виробничого планування складається у визначенні кількості виробів кожного виду, що повинно виробляти підприємство, щоб витрачання наявної сировини не перевищувало її запасів, а доход підприємства був би якнайбільше, тобто досягав максимуму. Приймемо такі позначення:
Дуже зручною формою запису умови задачі є таблиця наступного виду. Таблиця 1
За невідомі у задачах лінійного програмування беруть ті величини, які потрібно визначити. У даній задачі:
Складемо обмеження. Якщо на один виріб I виду витрачається
– ця величина складається з витрат сировини I виду по кожному виду продукції. Оскільки запаси обмежені, то ця сума не повинна перевищувати величину запасу по цьому виду сировини (тобто повинна бути менше її чи дорівнювати їй):
Аналогічно для другої сировини: варто врахувати витрачання цієї сировини по усіх виробах кожного виду, а потім знайти сумарну витрату, і ця витрата сировини II виду не повинна перевершувати запаси сировини цього виду. Тим самим одержимо друге обмеження
Провівши подібні міркування для усіх видів сировини, одержимо систему обмежень, що описує дану задачу:
……………………………………..
Оскільки число виробів будь-якого виду не може бути від’ємним, вимагаємо, щоб усі введені невідомі були більше нуля, або у крайньому випадку, дорівнювали нулю. Доход, одержуваний від виробництва усіх виробів першого виду, складає Таким чином, задача полягає в знаходженні таких змінних
і перетворюють функцію доходу
Транспортна задача. Нехай у пунктах Транспортна задача полягає в розподілі виробленого продукту так, щоб попит був вдоволений і сумарні транспортні витрати були мінімальними. Приймемо позначення:
Складемо таблицю. Вона дасть нам більш чітке уявлення про задачу. Таблиця 2
Особливістю транспортної задачі є наявність великого числа чинників, тому має сенс впроваджувати подвійні індекси. Позначимо через
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 252; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.221.81.158 (0.016 с.) |

 видів сировини для виробництва
видів сировини для виробництва  видів виробів. Заздалегідь відомі норми витрачання кожного виду сировини на виготовлення одиниці кожного виду виробу. Крім того, відомі запаси кожного виду сировини і доход підприємства від реалізації одиниці виробів кожного виду.
видів виробів. Заздалегідь відомі норми витрачання кожного виду сировини на виготовлення одиниці кожного виду виробу. Крім того, відомі запаси кожного виду сировини і доход підприємства від реалізації одиниці виробів кожного виду. –
–
 -го виду
-го виду  ;
;
 –
–
 -го виробу
-го виробу  ;
;
 –
–










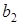









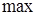
 –
–
 –
–
 –
–
 –
–





 ; від виробництва виробів другого виду –
; від виробництва виробів другого виду –  і т.д. і від виробництва виробів
і т.д. і від виробництва виробів  . Загальний доход виразиться у виді суми цих величин.
. Загальний доход виразиться у виді суми цих величин. , котрі задовольняють умовам
, котрі задовольняють умовам
 ,
,  , …,
, …, 
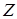 =
=  виробляється деякий однорідний продукт, причому обсяг виробництва (потужність) у кожнім пункті відомий. Цей продукт споживається в пунктах
виробляється деякий однорідний продукт, причому обсяг виробництва (потужність) у кожнім пункті відомий. Цей продукт споживається в пунктах  , при цьому відомий обсяг споживання (попит) для кожного пункту. Передбачається, що сумарна потужність дорівнює сумарному попиту. Припустимо, що транспортування можливе з будь-якого пункту виробництва в кожен пункт споживання, причому транспортні витрати, що приходяться на одиницю продукту, вважаються заданими. (Під транспортними витратами розуміють час перевозу, відстань, вартість).
, при цьому відомий обсяг споживання (попит) для кожного пункту. Передбачається, що сумарна потужність дорівнює сумарному попиту. Припустимо, що транспортування можливе з будь-якого пункту виробництва в кожен пункт споживання, причому транспортні витрати, що приходяться на одиницю продукту, вважаються заданими. (Під транспортними витратами розуміють час перевозу, відстань, вартість). –
–
 ;
;
 –
–
 –
–




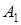




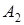






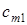


 – кількість продукту, перевезеного з першого пункту виробництва в перший пункт споживання, через
– кількість продукту, перевезеного з першого пункту виробництва в перший пункт споживання, через 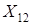 – кількість продукту, перевезеного з першого пункту виробництва в другий пункт споживання, і т.д.,
– кількість продукту, перевезеного з першого пункту виробництва в другий пункт споживання, і т.д.,  – кількість продукту, перевезеного з
– кількість продукту, перевезеного з 


