
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Дробово-лінійне програмуванняСодержание книги Поиск на нашем сайте
Якщо в задачі з лінійними обмеженнями задана дробово-лінійна цільова функція, то така задача може бути перетворена до традиційного виду шляхом нескладних змін. Перетворена модель може бути розв’язана симплексним методом, а знайдене рішення трансформоване в рішення вихідної задачі дробово-лінійного програмування. Всі етапи алгоритму проілюструємо на конкретному прикладі.
1. Систему обмежень приводять до канонічного виду:
2. Знаменник цільової функції позначають через § з’явиться додаткове обмеження § функція цілі стане такою 3. Всі обмеження множать на
4. Впроваджують позначення:
Упорядковують систему щодо нових змінних, переносячи з правої частини елементи, пов’язані з
5. Задача придбала канонічну форму, її рішення може бути виконано симплексним методом. З огляду на те, що індекси векторів повинні відповідати індексам змінних (
Таблиця 1 Початкове симплекс-рішення
Даній таблиці відповідають такі значення змінних:
Це рішення не оптимальне. У таблиці 1 отримано три однакових симплексних відношення, – усі вони дорівнюють нулю. При виборі ключового рядка керуються правилом: беруть той, що відповідає більшому елементу ключового стовпця. У даному випадку вибирають перший рядок, і генеральний елемент дорівнює 6.
Таблиця 2 Друга симплексна таблиця
Друге рішення виглядає так:
Воно не оптимальне. Перехід до третьої таблиці виконується за звичайними правилами з урахуванням коментарю до вибору ключового рядка, зробленого після таблиці 1. Таблиця 3 Третє симплексне рішення
Третє рішення:
Умова оптимальності все ще не виконується, переходять до наступної таблиці. Аналіз показує, що значення більшості змінних будуть дорівнювати нулю доти, поки ключовим рядком буде залишатися рядок з нульовим елементом у Таблиця 4 Четверте симплексне рішення
Рішення, що відповідає таблиці 4, має вигляд:
Воно не оптимальне, знаходять слідуюче симплекс-перетворення. Таблиця 5 П’яте симплексне рішення
У таблиці 5 отримане рішення, що задовольняє умові оптимальності:
6. Визначають значення вихідних змінних:
Таким чином, рішення задачі дробово-лінійного програмування буде наступним:
7. Дають, якщо можливо, геометричну інтерпретацію задачі: § знаходять область припустимих значень; § відзначають точки, що відповідають симплекс-таблицям.
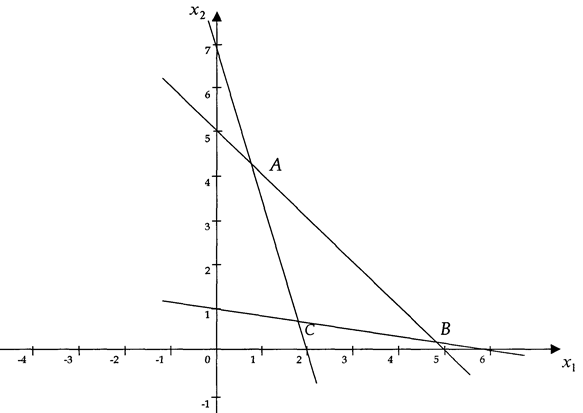
Областю рішень є трикутник
Зауваження. Дробово-лінійну задачу з двома змінними можна вирішувати графічним методом, ґрунтуючись на таких правилах: 1. По системі заданих обмежень будують область припустимих рішень. 2. Вибирають довільне значення 3. Позначимо § якщо § якщо 4. Визначивши оптимальні точки, знаходять їх координати – це і будуть оптимальні значення змінних, після чого обчислюють величину функції цілі. Приклад. Знайти рішення дробово-лінійної задачі.
1. Будуємо область припустимих рішень – вона визначається трьома нерівностями і являє собою трикутник
2. Будуємо пряму а) б)
а) б)
Параметричне програмування
Існує значна група економічних задач, у яких до складу лінійної цільової функції чи правої частини обмежуючих умов входить параметр. Наприклад, якщо ефективність або доход залежать від сезонних коливань, тоді критерій оптимальності повинний цю залежність відображати. Якщо постачання ресурсів також змінюється під впливом якихось причин, то в системі обмежень це повинно відобразитися. Якщо продукція, що виготовлена підприємством, повинна якийсь час зберігатися, то її вартість складається з двох частин: постійної – це вартість продукції на момент виготовлення – і змінної частини, що залежить від терміну зберігання, причому ця залежність, як правило, лінійна. Цільова функція задачі оптимального планування такого виробництва буде мати коефіцієнти, що лінійно залежать від параметра
Головна ідея методу рішення таких задач складається з двох частин: § беруть фіксовану величину параметра § визначають усі значення параметра Ці дві частини методу повторюють доти, поки не будуть знайдені рішення для усіх 1. Задачу готують до рішення: функцію спрямовують до мінімуму; нерівності перетворять у рівняння, вводячи додаткові змінні; вводять штучні змінні, якщо потрібно. 2. Надають параметру 3. Будують І симплексну таблицю відповідно до правил. 4. Доповнюють І симплекс-таблицю двома рядками. В 5. Проводять розрахунки всіх елементів таблиці відповідно до правил симплексного методу, перевіряючи оптимальність на основі М-рядка, а потім 6. Виписують оптимальне рішення, якщо критерій ефективності виконався. Після цього рядок 7. Знаходять для а) усі
б) усі
в)
8. Якщо отриманий інтервал не охоплює відрізок 9. Наступний етап полягає у виборі ключового стовпця – їм буде стовпець, у якому отримане значення Приклад. Знайти рішення задачі параметричного програмування
Підготуємо задачу до рішення:
Надамо параметру
Сформуємо 1 симплекс-таблицю з додатковими рядками: Таблиця 1
Критерій оптимальності не виконується. У таблиці 1 ключовими будуть стовпець Таблиця 2
У таблиці 2 критерій оптимальності не виконується. У новий базис входить Таблиця 3
У таблиці 3 досягнуто мінімум
Це рішення визначає вершину
Виходить, вершина Таблиця 4
У таблиці 4 отримане нове рішення:
Воно визначає вершину
Таким чином, у точці Таблиця 5
У таблиці 5 отримане таке рішення:
Підводячи підсумки, конкретизуємо висновки: § якщо § якщо § якщо Якщо дати геометричну інтерпретацію результатам рішення, то одержимо таку картину. П’ятикутник
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 627; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.188.114.205 (0.012 с.) |


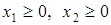
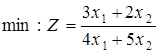
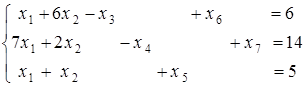
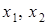
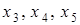
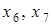
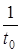 , це приводить до наступного:
, це приводить до наступного: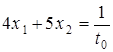 або
або 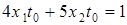 ;
;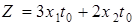 .
.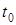 і до них додають додаткове співвідношення.
і до них додають додаткове співвідношення.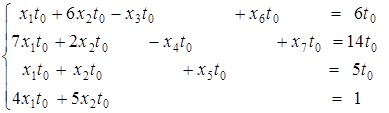
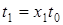 ;
; 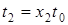 ;
; 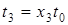 ;
;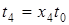 ;
;  ;
; 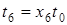 ;
; 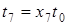 .
.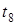 . Це необхідно для формування початкового базису. У результаті зазначених перетворень задача здобуває вигляд:
. Це необхідно для формування початкового базису. У результаті зазначених перетворень задача здобуває вигляд:

 ,
, 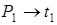 ,
,  і т.д.), вектор вільних членів позначають через
і т.д.), вектор вільних членів позначають через 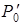 - це позбавить від плутанини.
- це позбавить від плутанини.
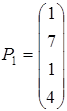

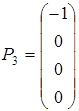
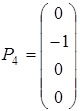
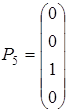

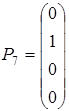
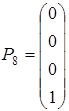


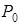
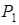
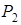


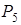
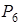
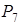

 -рядок
-рядок
 ;
;  ;
; 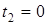 ;
; 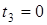 ;
; 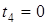 ;
; 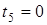 ;
; 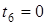 ;
; 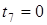 ;
; 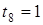 .
.

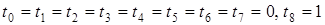 .
.
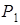
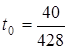 ,
, 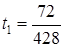 ,
, 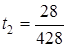 ,
, 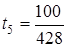 ,
, 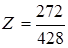 .
. ,
,  ,
, 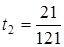 ,
, 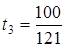 ,
,  .
.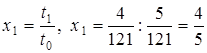 ;
;  ;
; 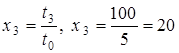 .
.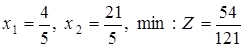 .
.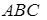 . Перші реальні значення змінних
. Перші реальні значення змінних 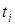 з’явилися в четвертій симплексній таблиці, їм відповідають такі значення вихідних невідомих:
з’явилися в четвертій симплексній таблиці, їм відповідають такі значення вихідних невідомих:  . На графіку – це вершина
. На графіку – це вершина 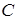 , вона не є оптимальної. Оптимальне рішення забезпечує вершина
, вона не є оптимальної. Оптимальне рішення забезпечує вершина  .
.
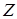 і будують відповідну пряму
і будують відповідну пряму 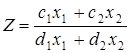
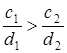 , то, повертаючи пряму
, то, повертаючи пряму 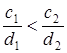 , то для одержання мінімуму пряму
, то для одержання мінімуму пряму 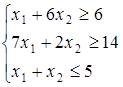
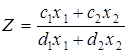 , розглянемо 2 варіанти функції
, розглянемо 2 варіанти функції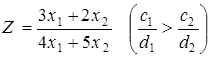

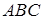 .
.
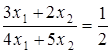
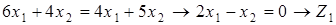

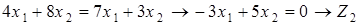
 ;
;  ;
; 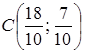
 ;
; 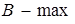 ;
; 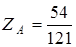 ;
; 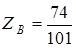 ;
; 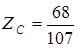
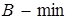 ;
;  ;
;  ;
; 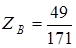 ;
; 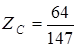
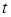 (від часу).
(від часу).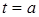 ); тоді всі коефіцієнти функції цілі будуть постійними; вирішують задачу для цього випадку, тобто знаходять вершину, у якій досягнуто екстремум;
); тоді всі коефіцієнти функції цілі будуть постійними; вирішують задачу для цього випадку, тобто знаходять вершину, у якій досягнуто екстремум;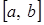 ; для інтервалу, що залишився, знову вирішують задачу.
; для інтервалу, що залишився, знову вирішують задачу.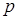 -рядку записують із протилежним знаком коефіцієнти цільової функції, не зв'язані з параметром
-рядку записують із протилежним знаком коефіцієнти цільової функції, не зв'язані з параметром 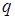 -рядок вносять із протилежним знаком коефіцієнти функціонала, що знаходяться перед параметром
-рядок вносять із протилежним знаком коефіцієнти функціонала, що знаходяться перед параметром 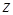 -рядка.
-рядка. - початок інтервалу,
- початок інтервалу, 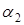 - кінець інтервалу):
- кінець інтервалу):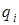 додатні
додатні 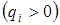 – у цьому випадку частковий інтервал визначається таким способом:
– у цьому випадку частковий інтервал визначається таким способом:
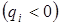 – у цьому випадку інтервал сталості рішення знаходиться так:
– у цьому випадку інтервал сталості рішення знаходиться так:
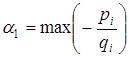 для
для 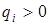
 для
для 
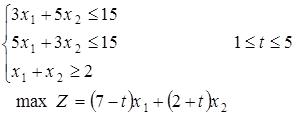
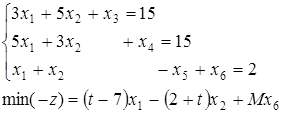
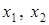

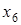
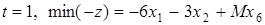
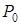
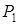
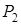
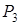
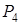
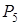

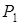 і третій рядок. У базис входить вектор
і третій рядок. У базис входить вектор 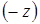 і максимум
і максимум 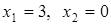 .
.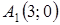 . Воно буде зберігатися для деяких значень
. Воно буде зберігатися для деяких значень 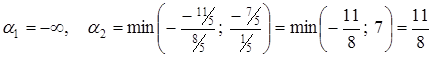 .
.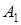 забезпечує максимум для
забезпечує максимум для  . Цей інтервал не перекриває відрізок
. Цей інтервал не перекриває відрізок 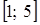 , тому рішення треба продовжити. Ключовим стовпцем буде стовпець
, тому рішення треба продовжити. Ключовим стовпцем буде стовпець 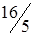 . Усі розрахунки виконуємо відповідно до правил симплексного методу. Одержимо таблицю 4.
. Усі розрахунки виконуємо відповідно до правил симплексного методу. Одержимо таблицю 4.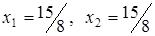 .
.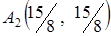 . Ця вершина буде забезпечувати оптимальність для інших значень
. Ця вершина буде забезпечувати оптимальність для інших значень 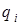 мають різні знаки:
мають різні знаки: .
.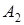 досягається максимум, якщо
досягається максимум, якщо 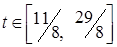 . Цей інтервал теж не охоплює значення відрізка
. Цей інтервал теж не охоплює значення відрізка  . Одержимо таблицю 5.
. Одержимо таблицю 5.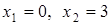 . Воно відповідає вершині
. Воно відповідає вершині 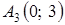 . Оскільки всі
. Оскільки всі  , у відповідності з випадком б) пункту 7, буде оптимальною для наступних значень
, у відповідності з випадком б) пункту 7, буде оптимальною для наступних значень 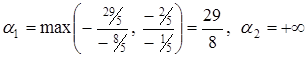 .
.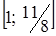 , то цільова функція досягає максимуму в точці
, то цільова функція досягає максимуму в точці 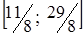 , то максимум буде у вершині
, то максимум буде у вершині  до 5, то максимум досягається в точці
до 5, то максимум досягається в точці 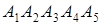 є безліччю припустимих рішень системи обмежень. З урахуванням відрізка зміни параметра
є безліччю припустимих рішень системи обмежень. З урахуванням відрізка зміни параметра 


