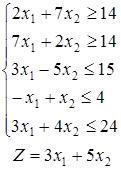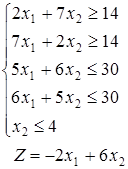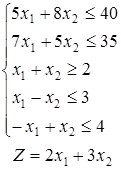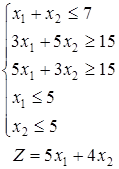Приклади задач лінійного програмування

1-30. Виконати математичну постановку задач.

 

Задача 1.	Два постачальники забезпечують товаром трьох споживачів. У таблиці зазначені транспортні витрати на перевіз одиниці продукції від кожного постачальника кожному споживачу.
	Постачальники	Споживачі	Наявність
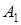
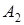
	Потреба

 

Поставити задачу в математичній формі, прагнучи до мінімізації транспортних витрат.

 

Задача 2.	Для виготовлення столів і шаф застосовується три види деревини. Витрати деревини для кожного виробу наведені у таблиці.
	Виріб	Вид деревини
	I	II	III
	Стіл, м ^3	0,2	0,2	0,25
	Шафа, м ^3	0,3	0,25	0,25
	Запаси деревини, м ^3

 

Доход від реалізації одного столу складає 30 грн., а шафи – 42 грн. Поставити задачу математично, максимізуючи доход.

 

Задача 3.	Припустимі варіанти розкрою довгомірного матеріалу довжиною 7,4 м на заготівки розміром 1,5; 2,1; 2,9 м представлені в таблиці
	Довжина заготівок, мм	Число заготівок, що викроюються по варіантах
	I	II	III	IV	V	VI
				-		-
		-	-
					-
	Використовується мм
	Остача мм

Здійснити розкрій при мінімальних відходах матеріалу. Виконати математичну постановку задачі, з огляду на те, що заготівок I виду повинно бути не менше 300, II виду – не менше 420, а III – не менше 570.

 

Задача 4.	Розподілити деталі за машинами таким чином, щоб на їхню обробку було витрачено мінімум часу. Представити задачу математично. У таблиці приведені всі необхідні дані.
	Деталь машини	Норма часу на обробку	Резерв часу машини
	1	2	3	4	5	6
	Необхідне число деталей

 

Задача 5.	Побудувати план перегону порожніх товарних вагонів з пунктів відправлення в пункти призначення, щоб сумарні витрати на перегін були мінімальними. У таблиці приведені витрати на перегін одного вагона.
	Пункти призначення Пункти відправлення						Запаси вагонів
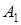
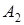
	Потреба у вагонах

 

Задача 6.	Скласти оптимальний добовий раціон відгодівлі свиней, якщо раціон однієї голови повинний містити кормових одиниць 2,3 кг, протеїну – 270 г, каротину – 48 г. Раціон складається з трьох видів кормів: ячменя, бобів, сінного борошна. У 1 кг ячменя міститься кормових одиниць 1,2 кг, протеїну – 80г, каротину – 12 г; у 1 кг бобів відповідно – 1, 25 кг, 280 г і 10г; у 1 кг сінного борошна відповідної 0,75 кг, 100 г і 20 г. Ціна 1 кг ячменя – 3 грн, бобів – 14 грн, сінного борошна – 8 грн. Критерій оптимальності – мінімум вартості раціону.
Задача 7.	На трьох групах обладнання необхідно виготовити вироби чотирьох видів. Установлено план виробництва: виробів типу А – 2000 шт., Б – 1000 шт., В – 200 шт., Г – 250 шт. Дані про собівартість виготовлення кожного виробу, трудомісткість і фонд робочого часу містяться в таблиці.
	Вид обладнання	Собівартість, грн.	Час на один виріб	Фонд часу, години
	A	Б	В	Г	A	Б	В	Г
	I
	II
	III

 

Скласти модель задачі, яка мінімізує витрати на виконання виробничої програми.

 

Задача 8.

Арматурний цех заводу одержує пруток довжиною 5 м. Необхідно випустити 350 заготівок довжиною 2,4 м, 500 заготівок довжиною 1,6 м і 750 заготівок довжиною 1,3 м. Скласти різні варіанти розкрою і побудувати модель мінімізації відходів при виконанні виробничої програми.

 

Задача 9.	На будівельній ділянці є 5 екскаваторів, що можуть бути використані на 5-ти будівельних об'єктах. Собівартість (грн./година) земельних робіт зазначена в таблиці.
	Тип екскаватора	Будівельний об'єкт
	1	2	3	4	5
	А
	Б
	В
	Г
	Д

 

Необхідно задачу розподілу екскаваторів поставити математично, домагаючись мінімальної собівартості. (Екскаватори між об'єктами протягом зміни не переміщають).

 

Задача 10.	Підприємство має три групи устаткування і може випускати на ньому чотири види продукції. Трудомісткість обробки кожного виробу на різному устаткуванні і прибуток приведені в таблиці.
	Номер виробу	Трудомісткість обробки по групах устаткування /година	Прибуток за штуку	Мінімальний обсяг реалізації, шт.
	I	II	III
	Фонд часу, година				-	-

 

Виходячи з вимоги максимізації прибутку, сформувати модель розподілу виробів по різних групах устаткування.

 

Задача 11.	Розподілити площу для сівби під різні культури, щоб валова продукція у вартісному вираженні була найбільшою. Виразити задачу в математичній формі, якщо в таблиці зазначені витрати праці на кожну культуру.
	Показники	Ячмінь	Цукровий буряк	Виробничі ресурси
	Витрати на механізованих роботах, година	0,6	4,5
	Витрати кінно-ручної праці, година
	Ціна 1 центнера продукції, грн.			-

Урожайність ячменя складає 25 ц з гектара, буряка – 80 ц.

 

Задача 12.	У таблиці зазначені транспортні витрати на перевіз одиниці вантажу від кожного постачальника до кожного споживача, а також їхні пропозиції та попит.
	Споживач   Постачальники	Вартість перевезення одиниці	Мається в наявності
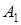
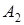
	Потреба

 

Побудувати математичну модель транспортної задачі, керуючись мінімумом витрат.

 

Задача 13.	Три сорти палива в кількостях 40, 70 і 50 т. розподілити між чотирма агрегатами, потреби яких рівні 60, 30, 45 і 25 т. відповідно. Задано матрицю теплотворної здатності кожного палива в кожнім агрегаті:
	.

Поставити задачу про розподіл палива між агрегатами у формі математичної моделі, ціль якої – максимальна кількість тепла від запасу палива.

 

Задача 14.	Фабрика випускає шкіряні штани, куртки, пальто. У процесі виготовлення вироби проходять три ділянки, час обробки і планова собівартість виробів приведені в таблиці. Обмеження на фонд часу на ділянках відповідно складають 4000, 4200 і 4400 годин.
	Показники	Штани	Куртки	Пальто
	Норма часу на дубильній ділянці	0,4	0,5	0,7
	Норма часу на розкрійній ділянці	0,5	0,3	0,8
	Час на пошивній ділянці	0,6	0,5	0,8
	Планова собівартість, грн.

 

Скласти модель випуску зазначених виробів, виходячи з вимог мінімізації собівартості продукції, що випускається, і необхідності забезпечення плану випуску 1800, 3600 і 1500 виробів відповідно.

 

Задача 15.	Підприємство одержує пруток довжиною 5 м для виготовлення заготівок довжиною 1,2 м, 0,8 м і 1,5 м, потреба в яких дорівнює відповідно не менш 800, 950, 1200 штук. Необхідно визначити, яку кількість прутків і якими способами треба нарізати заготівки, щоб відходи були мінімальними. Варіанти розкрою прутка на заготівки представлені в таблиці.
	Розмір заготівок	Варіанти розкрою
	1,2							-	-
	0,8	-						-
	1,5	-	-	-			-
	Відходи	0,2	0,6	0,2	0,3		0,6	0,5	0,4

 

Задача 16.	Три діючих цегельних заводи А, В и С мають денну продуктивність 80, 120 і 100 тис. штук цегли. Планована потреба в цеглі: у споживача I – 90 тис. штук, у II – 70 тис. штук, у III – 80 тис. штук, у IV – 60 тис. штук. Матриця транспортних витрат задана.
	Постачальники	Споживачі
	I	II	III	IV
	А
	В
	С

 

Скласти транспортну модель, прагнучи до мінімуму транспортних витрат.

 

Задача 17.	З трьох складів необхідно вивезти мінеральну воду в три торгові точки. Вартість перевезення 1 тис. пляшок представлена в таблиці.
	Пункт відправлення	Витрати на доставку 1 тис. пляшок у торгову точки	Обсяг вивозу, тис. пляшок
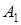
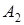
	Обсяг ввозу, тис. пляшок

 

Скласти план закріплення складів за торговими точками, що забезпечує мінімум витрат на перевезення.

 

Задача 18.	Будівельні організації споруджують будинки чотирьох різних типів: Д-1, Д-2, Д-3, Д-4. Дані про кількість квартир різного типу в кожнім з будинків приведені в таблиці.
	Показники	Д-1	Д-2	Д-3	Д-4
	Однокімнатні
	Двокімнатні суміжні
	Двокімнатні несуміжні
	Трикімнатні
	Чотирьохкімнатні
	Планова собівартість, тис. грн.

 

Річний план уведення житлової площі складає відповідно 1500, 840, 1740, 1950, 650 квартир зазначених типів. Скласти план будівництва житлових будинків, щоб загальна собівартість була найменшою. Записати задачу в канонічному вигляді.

 

Задача 19.	Цех меблевого комбінату випускає трельяжі, трюмо і тумбочки під телевізори. Норма витрати матеріалів, плановий асортимент і собівартість виробів наведені в таблиці.
	Показники	Трельяжі	Трюмо	Тумбочки	Запаси деревини
	Витрата деревних плит, м^3	0,032	0,031	0,038	99,8
	Витрата ялинових дощок, м^3	0,020	0,030	0,008	40,8
	Витрата березових дощок, м^3	0,005	0,005	0,006	15,6
	Плановий асортимент, штук				-
	Собівартість, грн.	38,8	64,0	29,6	-

 

Виходячи з необхідності виконання і перевиконання плану з асортименту, побудувати модель максимізації обсягу реалізації. Представити задачу в канонічному вигляді.

 

Задача 20.	В відповідності з планованим рівнем удою і вагою тварини одній корові необхідно в добу не менш 19,26 кормових од., 1926 г білка, 114 г кальцію і 85 г фосфору. У раціон годівлі входять: сіно конюшинове, сіно лугове, кормовий буряк, картопля, силос, концентрати. У таблиці приведені показники, що характеризують вміст харчувальних речовин у 1 кг кормів і ціни кормів. Скласти раціон, що задовольняє вимозі мінімальної вартості утримання худоби.
	Вид корму	Ціна корма, за 1 кг	Вміст
	Кормові одиниці	Білок, г	Кальцій, г	Фосфор, г
	Сіно коньошинове		0,54		9,29	1,95
	Сіно лугове		0,52		6,02	2,14
	Силос		0,18		3,55	0,65
	Буряк кормовий		0,12		0,38	0,33
	Картопля		0,30		0,14	0,68
	Концентрати		1,06		2,06	7,60

 

Задача 21.	До складу годівлі тварин входять три продукти: сіно, силос і концентрати, що містять харчувальні речовини: білок, кальцій і вітаміни. Вміст харчувальних речовин і мінімально необхідні норми їх споживання задані таблицею:
	Харчувальні речовини Продукти	Білок, г/кг	Кальцій, г/кг	Вітаміни, у.од./кг
	Сіно
	Силос
	Концентрати
	Норми споживання

 

Визначити оптимальний раціон годівлі в умовах мінімальної вартості, якщо ціна 1 кг відповідно складає: сіна – 3 грн., силосу – 2 грн., концентратів – 5 грн., при граничних нормах добової видачі: сіна – не більш 18 кг., силосу – не більш 24 кг і концентратів – не більш 16 кг і при вмісті харчувальних речовин у продуктах, зазначених у таблиці.

 

Задача 22.

Три види деталей можна робити на верстатах різних типів без переналагодження. Потужності верстатів, обмеження на робочий час і собівартість у грн. однієї деталі кожного виду зазначені в таблиці:

 

 

Вид деталей	Продуктивність станків, деталей за годину	Собівартість деталей
I тип	II тип

 

Фонд робочого часу для верстатів складає відповідно 12 і 8 годин. Потрібно розподілити робочий час верстатів з метою одержання мінімальної собівартості, якщо за планом за робочий день необхідно випустити не менш 160 деталей 1 виду, 120 – 2-го виду і не менш 240 – 3-го.

 

Задача 23.	Під посів пшениці, вівса і гречки відведено дві земельних ділянки площею в 120 і 150 га відповідно. У таблиці зазначена: середня врожайність кожної культури на кожній ділянці, виручка на 1 ц культур і варіанти планових завдань по виробництву.
	Культура	Врожайність по участках, ц/га	Виручка, грн.	Планове завдання, т
	I варіант	II варіант	I варіант	II варіант
	Пшениця
	Овес
	Гречка

 

1. Визначити, яку площу на кожній ділянці варто відвести під кожну з культур для одержання максимальної виручки, якщо встановлений I варіант плану.

2. Як зміниться виручка, якщо встановлений II варіант плану?

 

Задача 24.	Видавництво, параметри діяльності якого відбиті в таблиці, випускає літературу чотирьох серій.
	Серія Показник
	Прибуток від реалізації од. продукції, грн./екз.
	Собівартість од. продукції, грн./екз.
	Питома пропускна здатність друкарні, відбиток /екз.
	Питома витрата папера, лист /екз.

Видавництво має у своєму розпорядженні фонд фінансових кошт у 10000 грн., ліміти на папір у розмірі 90 000 аркушів і пропускну здатність друкарень, яка дорівнює 110000 відтисків. При яких тиражах серій, що випускаються, видавництво дістане максимальний прибуток?

 

Задача 25.	Адміністрація видавництва, що створюється, повинна вирішити питання про набір штату коректорів для кожної з чотирьох редакцій. При цьому фонд заробітної плати по видавництву не повинен перевершити 850000 грн., загальний час роботи всіх коректорів не повинен перевищити 50000 годин., сумарний ліміт матеріалів – не більш 50000 грн.
	Редакції Показники	I	II	III	IV
	Заробітна плата коректора, грн.
	Витрати часу коректора, час.
	Витрати матеріалу на людину, грн.
	Продуктивність коректора, лист

 

Використовуючи дану таблицю, дати рекомендацію керівництву видавництва, скільки коректорів у кожну редакцію воно повинно запросити, щоб випуск продукції в аркушах був максимальним.

 

Задача 26.	Книгарня, обсяг реалізації якої не перевищує 230000 аркушів друкованої продукції, забезпечується чотирма видавництвами. Складаючи план-замовлення кожному з них, магазин повинний врахувати ліміт витрат на папір у 33000 грн. і пропускну здатність обслуговуючої видавництво друкарні, рівну 100000 аркушам. Питомі витрати кожного ресурсу містить (по кожному видавництву) таблиця.
	Видавництва Показники	I	II	III	IV
	Питомий об’єм книг видавництва, листів/книг
	Питомі витрати паперу, грн./ книг
	Питомі друкарські витрати, листів/книг
	Прибуток від реалізації продукції, грн./ книг		4,5		3,5

Скільки книг магазин зможе прийняти від кожного видавництва, щоб його прибуток був найбільшим і величина обмежених ресурсів не був перевершений?

 

Задача 27.	Підприємство має у своєму розпорядженні ресурси сировини, робочої сили й устаткування, що необхідно для виробництва кожного з чотирьох видів продукції. Витрати ресурсів на виготовлення одиниці даного виду продукції, прибуток, одержуваний підприємством, а також запаси ресурсів зазначені в наступній таблиці:
	Види продукції Види ресурсів					Запаси ресурсів
	Сировина, кг
	Робоча сила, час.
	Устаткування, станко-час.
	Прибуток на од. продукції, грн.					-

 

Визначити, який асортимент продукції треба випускати, щоб прибуток був максимальним.

 

Задача 28.	Підприємство має три комплексні автоматичні лінії устаткування і може випускати вироби чотирьох типів – А, Б, В, Г. Відомі середні норми витрат часу на обробку кожного виду виробів на кожній лінії і прибуток від реалізації одиниці кожного виробу, вони приведені в наступній таблиці:
	Лінії устаткування	Витрати часу на одиницю виробу, мін.	Місячний фонд часу, год.
	А	Б	В	Г
	I лінія	1,0	2,0	4,0	8,0
	II лінія	3,0	5,0	1,0	-
	III лінія	6,0	-	3,0	1,0
	Прибуток від реалізації одиниці виробу, грн.					-

 

Яка найбільш рентабельна програма випуску виробів, якщо кожен виріб потрібно обробляти до готовності на декількох лініях?

 

Задача 29.	Тканина трьох артикулів виробляється на ткацьких верстатах двох видів з різною продуктивністю. Для виготовлення тканини використовується натуральне і синтетичне волокно. У таблиці зазначені потужності верстатів (у тис. станко-годин), ресурси натурального і синтетичного волокна (у тис. кг), продуктивності верстатів по кожному виду тканини (у м/година.), норма витрати волокна по видах (у кг на 1000 м) і ціна тканини кожного з артикулів (у грн.) за 1 м.
	Вид ресурса	Об’єм ресурса	Продуктивність і норми витрат
	1	2	3
	Верстати I типа		4,0	2,0	5,0
	Верстати II типа		1,6	4,0	2,0
	Натуральне волокно		24,0	36,0	42,0
	Синтетичне волокно		2,0	1,0	1,6
	Ціна тканини	-

 

Визначити оптимальний асортимент, що забезпечує прибуток підприємства. Як зміниться рішення, якщо для виробництва тканин першого і другого артикула не буде потрібно синтетичне волокно?

 

Задача 30.	Меблева фабрика випускає столи, стільці, одежні і книжкові шафи. При виготовленні цієї продукції використовується два типи деревних матеріалів. У таблиці приведені нормативи витрат кожного з матеріалів (м) і трудових ресурсів (люд.-година.) на виготовлення одиниці кожного виду продукції, а також прибуток від реалізації одиниці виробу і загальних обсягів наявних ресурсів кожного типу.
	Вироби   Ресурси	Витрати на одиницю виробу	Об’єм ресурсів
	столи	стільці	шафи одежні	шафи книжкові
	Деревина I типа, м
	Деревина II типа, м
	Трудові ресурси, люд.-час.
	Прибуток, грн.					-

Визначити:

§ Асортимент продукції, що максимізує прибуток фабрики в даних умовах.

§ Оптимальний асортимент за умови, що столів потрібно зробити не менш 40, стільців – не менш 120, одежних шаф – не менш 20 і книжкових шаф – не більш 20.

Графічний метод

1-30. Побудувати на площині область припустимих рішень системи лінійних нерівностей і геометрично знайти найменше і найбільше значення цільової функції, вважаючи , .

1.	2.	3.
4.	5.	6.
7.	8.	9.
10.	11.	12.
13.	14.	15.
16.	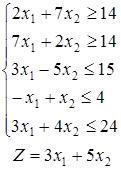17.	18.
19.	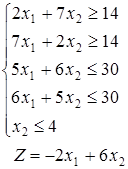20.	21.
22.	23.	24.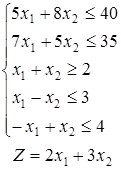
25.	26.	27.
28.	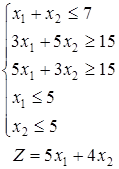29.	30.
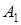
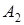