
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Две основные задачи динамики материальной точкиСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Две основные задачи динамики материальной точки Используя дифференциальные уравнения движения материальной точки (1.5), (1.10), (1.12) и (1.14), можно решить две основные задачи динамики точки, которые формулируют следующим образом. Первая задача. Определить силы, действующие на точку, если известны масса точки и закон ее движения. Решение этой задачи заключается, в основном, в определении ускорения точки по заданным уравнениям ее движения, т.е. в их дифференцировании. Можно предложить такую последовательность решения задачи: 1) выбрать систему координат, в которой удобно решать данную задачу (декартовую или естественную); 2) изобразить в выбранной системе координат материальную точку в текущем положении; 3) приложить к точке активные силы и реакции связей; 4) записать основное уравнение динамики в проекциях на оси выбранной системы координат; 5) найти проекции ускорения точки на оси выбранной системы координат путем дифференцирования уравнений ее движения; 6) определить искомые параметры с помощью системы составленных уравнений. Вторая задача. Определить закон движения точки, если заданы масса точки и действующие на нее силы. Решение этой задачи требует интегрирования дифференциальных уравнений движения точки. Методика решения второй задачи на примере декартовой системы координат состоит в следующем. Чтобы определить уравнения движения точки (1.15) где После определения постоянных интегрирования уравнения действительного движения точки окончательно получим в виде: Решение второй задачи динамики можно выполнить в такой последовательности: 1) выбрать систему координат (декартовую или естественную), в которой удобно решать данную задачу; 2) изобразить в выбранной системе координат материальную точку в текущем положении; 3) приложить к точке активные силы и реакции отброшенных связей (если точка несвободна); 4) записать основное уравнение динамики в проекциях на оси выбранной системы координат; 5) проинтегрировать полученную систему дифференциальных уравнений и найти их общие решения; 6) определить, использую заданные начальные условия, постоянные интегрирования; 7) подставить постоянные интегрирования в общие решения и получить действительные уравнения движения точки.
Дифференциальные уравнения движения точки
С помощью дифференциальных уравнений движения решается вторая задача динамики. Правила составления таких уравнений зависят от того, каким способом хотим определить движение точки. 1) Определение движения точки координатным способом. Рассмотрим свободную материальную точку, движущуюся под действием сил
Рис.4
Так как действующие на точку силы могут зависеть от времени, от положения точки и от ее скорости, то правые части уравнений могут содержать время t, координаты точки х, у, z и проекции ее скорости Чтобы с помощью этих уравнений решить основную задачу динамики, надо, кроме действующих сил, знать еще начальные условия, т.е. положение и скорость точки в начальный момент. В координатных осях Oxyz начальные условия задаются в виде: при
Зная действующие силы, после интегрирования уравнений найдем координаты х, y, z движущейся точки, как функции времени t, т.е. найдем закон движения точки.
Рис.10
Составим основное уравнение динамики для точки
Но
Спроектировав это векторное равенство на подвижные оси x 1, y 1, z 1, имея в виду, что проекции вектора ускорения на оси – есть вторые производные от соответствующих координат по времени, получим дифференциальные уравнения относительного движения
Сравнивая эти уравнения с дифференциальными уравнениями абсолютного движения, замечаем, что относительное движение материальной точки определяется такими же методами, что и абсолютное, надо лишь кроме обычных сил учесть переносную силу инерции и кориолисову силу инерции. Если переносное движение поступательное, равномерное и прямолинейное, т.е. подвижная система инерциальная, то ускорение Поэтому невозможно установить, наблюдая за движением точки, движется система поступательно, равномерно и прямолинейно или находится в покое. Этот вывод впервые был сделан Г.Галилеем и называется его именем – принцип относительности Галилея.
Масса системы. Центр масс. Движение системы, кроме действующих сил, зависит также от её суммарной массы и распределения масс. Масса системы равна арифметической сумме масс всех точек или тел, образующих систему
В однородном поле тяжести, для которого
В полученные равенства входят только массы Геометрическая точка С, координаты которой определяются указанными формулами, называется центром масс или центром инерции системы. Положение центра масс определяется его радиус-вектором
где Хотя положение центра масс совпадает с положением центра тяжести тела, находящегося в однородном поле тяжести, понятия эти не являются тождественными. Понятие о центре тяжести, как о точке, через которую проходит линия действия равнодействующей сил тяжести, по существу имеет смысл только для твердого тела, находящегося в однородном поле тяжести. Понятие же о центре масс, как о характеристике распределения масс в системе, имеет смысл для любой системы материальных точек или тел, причем, это понятие сохраняет свой смысл независимо от того, находится ли данная система под действием каких-нибудь сил или нет.
Рис.43 Аналогично происходит движение паровоза или автомобиля. Сила давления пара или газа в двигателе является силой внутренней и сама но себе не может переместить центр масс системы.Движение происходит потому, что двигатель передает соответствующим колесам, называемыми ведущими, вращающий момент. При этом точка касания В ведущего колеса (рис.43) стремится скользить влево. Тогда на колесо будет действовать сила трения, направленная вправо. Эта внешняя сила и позволит центру тяжести паровоза или автомобиля двигаться вправо. Когда этой силы нет или когда она недостаточна для преодоления сопротивления, испытываемого ведомыми колесами, движения вправо не будет; ведущие колеса будут при этом вращаться на месте (буксовать).
Рис.46
При вращении тела вокруг неподвижной точки кинетическая энергия определяется как (рис.47)
или, окончательно,
где Ix, Iy, Iz – моменты инерции тела относительно главных осей инерции x 1, y 1, z 1 в неподвижной точке О;
Рис.47
3. Плоскопараллельное движение. При этом движении скорости всех точек тела в каждый момент времени распределены так, как если бы тело вращалось вокруг оси, перпендикулярной к плоскости движения и проходящей через мгновенный центр скоростей Р (рис.46). Следовательно
где
Следовательно, при плоскопараллельном движении кинетическая энергия тела равна энергии поступательного движения со скоростью центра масс, сложенной скинетической энергией вращательного движения вокруг центра масс. 4) Для самого общего случая движения материальной системы кинетическую энергию помогает вычислить теорема Кенига. Рассмотрим движение материальной системы как сумму двух движений (рис.48). Переносного – поступательного движения вместе с центром масс С и относительного – движения относительно поступательно движущихся вместе с центром масс осей x 1, y 1, z 1. Тогда скорость точек
Рис.48
По определению центра масс его радиус-вектор в подвижной системе
Поэтому, окончательно, кинетическая энергия системы
Кинетическая энергия материальной системы равна сумме кинетической энергии при поступательном движении вместе с центром масс и кинетической энергии ее при движении относительно координатных осей, поступательно движущихся вместе с центром масс. В общем случае движения тела, которое можно рассматривать как сумму двух движений (переносного – поступательного вместе с центром масс С и относительного – вращения вокруг точки С), по теореме Кенига (1) получим
где Ix, Iy, Iz – главные центральные оси инерции тела. 52. Работа силы…
Для характеристики действия, оказываемого силой на тело при некотором его перемещении, вводится понятие о работе силы.
Рис.16
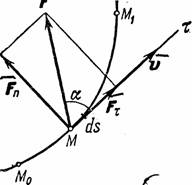
При этом работа характеризует то действие силы, которым определяется изменение модуля скорости движущейся точки. Введём сначала понятие об элементарной работе силы на бесконечно малом перемещении ds. Элементарной работой силы
где Данное определение соответствует понятию о работе, как о характеристике того действия силы, которое приводит к изменению модуля скорости точки. В самом деле, если разложить силу Замечая, что
Таким образом, элементарная работа силы равна проекции силы на направление перемещения точки, умноженной на элементарное перемещение Если угол Если угол Если угол Найдем аналитическое выражение элементарной работы. Для этого разложим силу
Рис.17
Элементарное перемещение Но на перемещении Формула дает аналитическое выражение элементарной работы силы. Работа силы на любом конечном перемещении М 0 М 1 вычисляется как интегральная сумма соответствующих элементарных работ и будет равна:
Следовательно, работа силы на любом перемещении М 0 М 1 равна взятому вдоль этого перемещения интегралу от элементарной работы. Пределы интеграла соответствуют значениям переменных интегрирования в точках М 0 и М 1.
Рис.18 Если величина Такой случай может иметь место, когда действующая сила постоянна по модулю и направлению (F = const), а точка, к которой приложена сила, движется прямолинейно (рис.18}. В этом случае Единицей измерения работы в системе СИ является джоуль (1 дж= 1 hm).
Работа силы упругости при одномерном растяжении (или сжатии), характеризующемся вектором удлинения (сжатия), Если одна из координатных осей (например, Ох) выбранной системы отсчета совпадает по направлению, с вектором, то где x1 и x2 — координаты начала и конца вектора. При перемещении точки упруго деформируемого тела по замкнутой траектории работа силы упругости равна нулю (Аупр = 0 при =0 или при x1 = x2). Рис.26
Дифференцируя выражение
Но
или В результате мы доказали следующую теорему моментов относительно центра: производная по времени от момента количества движения точки, взятого относительно какого-нибудь неподвижного центра, равна моменту действующей на точку силы относительно того же центра. Аналогичная теорема имеетместо для моментов вектора
Принцип Даламбера.
Все методы решения задач динамики, которые мы до сих пор рассматривали, основываются на уравнениях, вытекающих или непосредственно из законов Ньютона, или же из общих теорем, являющихся следствиями этих законов. Однако, этот путь не является единственным. Оказывается, что уравнения движения или условия равновесия механической системы можно получить, положив в основу вместо законов Ньютона другие общие положения, называемые принципами механики. В ряде случаев применение этих принципов позволяет, как мы увидим, найти более эффективные методы решения соответствующих задач. В этой главе будет рассмотрен один из общих принципов механики, называемый принципом Даламбера. Пусть мы имеем систему, состоящих из n материальных точек. Выделим какую-нибудь из точек системы с массой Введем в рассмотрение величину
имеющую размерность силы. Векторную величину, равную по модулю произведению массы точки на ее ускорение и направленную противоположно этому ускорению, называют силой инерции точки(иногда даламберовой силой инерции). Тогда оказывается, что движение точки обладает следующим общим свойством: если в каждый момент времени к фактически действующим на точку силам
Это выражение выражает принцип Даламбера для одной материальной точки. Нетрудно убедиться, что оно эквивалентно второму закону Ньютона и наоборот. В самом деле, второй закон Ньютона для рассматриваемой точки дает Повторяя проделанные высшее рассуждения по отношению к каждой из точек системы, придем к следующему результату, выражающему принцип Даламбера для системы: если в любой момент времени к каждой из точек системы, кроме фактически действующих на ней внешних и внутренних сил, приложить соответствующие силы инерции, то полученная система сил будет находиться в равновесии и к ней можно будет применять все уравнения статики. Значение принципа Даламбера состоит в том, что при непосредственном его применении к задачам динамики уравнения движения системы составляются в форме хорошо известных уравнений равновесия; что делает единообразный подход к решению задач и обычно намного упрощает соответствующие расчёты. Кроме того, в соединении с принципом возможных перемещений, который будет рассмотрен в следующей главе, принцип Даламбера позволяет получить новый общий метод решения задач динамики. Применяя принцип Даламбера, следует иметь в виду, что на точку механической системы, движение которой изучается, действуют только внешние и внутренние силы Из статики известно, что геометрическая сумма сил, находящихся в равновесии, и сумма их моментов относительно любого центра О равны нулю, причём по принципу отвердевания это справедливо для сил, действующих не только на твёрдое тело, но и на любую изменяемую систе6му. Тогда на основании принципа Даламбера должно быть:
Введём обозначения:
Величины
Применение уравнений (1), вытекающих из принципа Даламбера, упрощает процесс решения задач, т.к. эти уравнения не содержат внутренних сил. В проекциях на оси координат эти равенства дают уравнения, аналогичные соответствующим уравнениям статики. Чтобы пользоваться этими уравнениями при решении задач, надо знать выражение главного вектора и главного момента сил инерций.
Рис. 63
Таким образом, возможным перемещением системы мы будем называть любую совокупность бесконечно малых перемещений точек системы, допускаемых в данный момент всеми наложенными на систему связями. Возможное перемещение любой точки системы будем изображать элементарным вектором В общем случае для точек и тел системы может существовать множество возможных различных перемещений (перемещения Число независимых между собою возможных перемещений системы называется числом степеней свободы этой системы.Так, рассмотренный выше шарик на плоскости (или на поверхности), если его считать материальной точкой, имеет 2 степени свободы. У кривошипно-шатунного механизма будет, очевидно, одна степень свободы. У свободной материальной точки – 3 степени свободы (независимыми будут 3 перемещения вдоль взаимно перпендикулярных осей). Свободное твердое тело имеет 6 степеней свободы (независимыми перемещениями будут: 3 поступательных перемещения вдоль осей координат и 3 вращательных вокруг этих осей). К этому следует добавить несколько замечаний. Первое. Само название таких перемещений показывает, что они только возможны, но не обязательны; что этих перемещений из данного положения системы может быть много; что среди них только одно есть действительное (Если связи – не стационарные, изменяются с течением времени, то действительное перемещение может не быть одним из возможных); что эти перемещения происходят не под действием сил, приложенных к системе, а, так сказать, по нашему желанию. Второе. За счет малости таких перемещений направляются они по касательной к траектории и имеют, таким образом, направление, совпадающее с вектором скорости. Эту скорость в данном случае также называют возможной скоростью, а не действительной. Третье. При наличии связей между точками материальной системы, возможные перемещения этих точек связаны между собой определенными зависимостями, уравнениями связей. На рис.64 дано несколько примеров возможных перемещений точек некоторых материальных систем. Из этих примеров следует, что возможным перемещением всего тела, вращающегося вокруг оси, является малый угол поворота
Рис.64
Так как направления возможных перемещений имеют направления скоростей, то перемещения точек звена АВ (рис.64, в) определяются с помощью мгновенного центра скоростей Так как Аналогично, поворотом на малый угол Работу сил, приложенных к материальной системе, на возможном перемещении будем называть возможной работой. Если рассмотреть различные типы материальных систем, можно обнаружить, что элементарная работа реакций многих связей на возможном перемещении окажется равной нулю. Такие связи, сумма возможных работ реакций которых на любом возможном перемещении равна нулю, называются идеальными связями. К таким связям относятся, например, все связи без трения. Связи, которые не изменяются со временем, называются стационарными. Есть связи, которые называют или удерживающими, или односторонними, в зависимости от того препятствуют они перемещению точки во взаимно противоположных направлениях или только в одном. У некоторых материальных систем встречаются и довольно сложные связи, ограничивающие или только положение системы, координаты ее точек, или еще и скорость их, производные от координат по времени. Первые называют голономными, геометрическими, связями; вторые – неголономными, кинематическими, неинтегрируемыми. Мы в дальнейшем будем рассматривать системы только с голономными связями. Рис.65
Дадим системе какое-нибудь возможное перемещение. Все точки ее получат перемещения Затем вычислим работу всех сил на этих перемещениях. Так как силы, приложенные к каждой точке уравновешиваются и
Если связи идеальные, то вторая сумма всегда равна нулю. Значит,
Этот результат, уравнение работ, называют общим уравнением статики. При равновесии материальной системы с идеальными и стационарными связями сумма работ всех активных, задаваемых, сил на любом возможном перемещении системы из положения равновесия равна нулю. Конечно, если у системы есть неидеальные связи, например, с трением, или упругие, вроде пружины, то в уравнение работ надо добавить возможную работу реакций этих связей. Принцип возможных перемещений можно записать в другой форме. Если возможные перемещения точек определить с помощью возможных скоростей:
где | ||||
|
| Поделиться: |

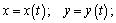
 , необходимо дважды проинтегрировать систему трех дифференциальных уравнений 2-го порядка. В результате получим уравнения движения точки, содержащие, кроме времени, шесть произвольных постоянных. Уравнения движения точки и проекции ее скорости на оси координат имеют вид:
, необходимо дважды проинтегрировать систему трех дифференциальных уравнений 2-го порядка. В результате получим уравнения движения точки, содержащие, кроме времени, шесть произвольных постоянных. Уравнения движения точки и проекции ее скорости на оси координат имеют вид: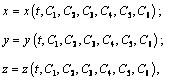

 – это так называемые постоянные интегрирования, которые находят из начальных условий. Начальные условия – значение скорости (проекций скорости) и положения (координат) точки в момент времени, обычно принимаемый равным нулю, которые должны быть предварительно заданы:
– это так называемые постоянные интегрирования, которые находят из начальных условий. Начальные условия – значение скорости (проекций скорости) и положения (координат) точки в момент времени, обычно принимаемый равным нулю, которые должны быть предварительно заданы: (1.16)
(1.16) (1.17)
(1.17) ,
,  ,..,
,..,  . Проведем неподвижные координатные оси Oxyz (рис.4). Проектируя обе части равенства
. Проведем неподвижные координатные оси Oxyz (рис.4). Проектируя обе части равенства  на эти оси и учитывая,что
на эти оси и учитывая,что 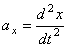 и т.д., получим дифференциальные уравнения криволинейного движения точки в проекциях на оси прямоугольной декартовой системы координат:
и т.д., получим дифференциальные уравнения криволинейного движения точки в проекциях на оси прямоугольной декартовой системы координат: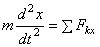 ,
,  ,
, 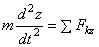 .
.
 . При этом в правую часть каждого из уравнений могут входить все эти переменные.
. При этом в правую часть каждого из уравнений могут входить все эти переменные.
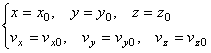 .
. , где абсолютное ускорение
, где абсолютное ускорение  . Поэтому уравнение будет таким
. Поэтому уравнение будет таким  или
или  .
.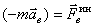 - переносная сила инерции,
- переносная сила инерции, 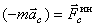 - кориолисова сила инерции. Поэтому основное уравнение динамики для относительного движения запишем так
- кориолисова сила инерции. Поэтому основное уравнение динамики для относительного движения запишем так . (7)
. (7) (8)
(8) и
и  . Значит
. Значит  и дифференциальное уравнение (8) будет точно совпадать с дифференциальным уравнением абсолютного движения. Следовательно, движение точки во всех инерциальных системах описывается аналогичными законами (отличаются только постоянными интегрирования, зависящими от начальных условий).
и дифференциальное уравнение (8) будет точно совпадать с дифференциальным уравнением абсолютного движения. Следовательно, движение точки во всех инерциальных системах описывается аналогичными законами (отличаются только постоянными интегрирования, зависящими от начальных условий).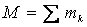 .
.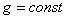 , вес любой частицы тела будет пропорционален ее массе. Поэтому о распределении масс в теле можно судить по положению его центра тяжести. Преобразуем формулы, определяющие координаты центра тяжести:
, вес любой частицы тела будет пропорционален ее массе. Поэтому о распределении масс в теле можно судить по положению его центра тяжести. Преобразуем формулы, определяющие координаты центра тяжести: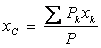 ,
, 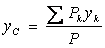 ,
,  . (1)
. (1)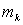 материальных точек (частиц), образующих тело, и координаты
материальных точек (частиц), образующих тело, и координаты 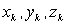 этих точек. Следовательно, положение точки С (x C, y C, z C) действительно характеризует распределение масс в теле или в любой механической системе, если под
этих точек. Следовательно, положение точки С (x C, y C, z C) действительно характеризует распределение масс в теле или в любой механической системе, если под 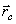
 ,
,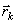 -радиус-векторы точек, образующих систему.
-радиус-векторы точек, образующих систему.
 ,
, ,
, 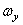 ,
,  – проекции вектора мгновенной угловой скорости
– проекции вектора мгновенной угловой скорости  на эти оси.
на эти оси.
 ,
,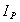 - момент инерции тела относительно названной выше оси, w- угловая скорость тела. Величина
- момент инерции тела относительно названной выше оси, w- угловая скорость тела. Величина  , относительно оси, проходящей через центр масс С тела. По теореме Гюйгенса
, относительно оси, проходящей через центр масс С тела. По теореме Гюйгенса  , где d=PC. Подставим это выражение для
, где d=PC. Подставим это выражение для  , где
, где  - скорость центра масс С, окончательно найдем:
- скорость центра масс С, окончательно найдем: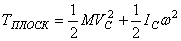 .
.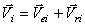 . Но переносное движение – поступательное. Поэтому переносные скорости всех точек равны, равны
. Но переносное движение – поступательное. Поэтому переносные скорости всех точек равны, равны  . Значит,
. Значит,  и кинетическая энергия будет
и кинетическая энергия будет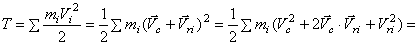
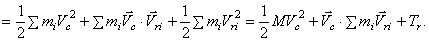

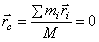 (центр масс находится в начале координат), значит, и
(центр масс находится в начале координат), значит, и  . Производная по времени от этой суммы также равна нулю:
. Производная по времени от этой суммы также равна нулю: .
. (1)
(1) или
или  ,
,
 (рис.16) называется скалярная величина:
(рис.16) называется скалярная величина: ,
,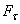 - проекция силы
- проекция силы  -бесконечно малое перемещение точки, направленное вдоль этой касательной.
-бесконечно малое перемещение точки, направленное вдоль этой касательной. и
и 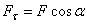 , получаем:
, получаем: . (1)
. (1) острый, то работа положительна. В частности, при
острый, то работа положительна. В частности, при  элементарная работа
элементарная работа  .
. элементарная работа
элементарная работа 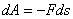 .
. , т.е. если сила направлена перпендикулярно перемещению, то элементарная работа силы равна нулю.
, т.е. если сила направлена перпендикулярно перемещению, то элементарная работа силы равна нулю. ,
,  ,
,  по направлениям координатных осей (рис.17; сама сила
по направлениям координатных осей (рис.17; сама сила 
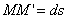 слагается из перемещений
слагается из перемещений  ,
, 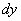 ,
,  вдоль координатных осей, где x, y, z - координаты точки М. Тогда работу силы
вдоль координатных осей, где x, y, z - координаты точки М. Тогда работу силы  . Работа на перемещениях
. Работа на перемещениях  .
.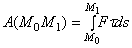
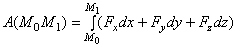 .
.
 получим:
получим: 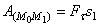 .
. и работа силы
и работа силы  .
.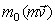 по времени, получаем:
по времени, получаем: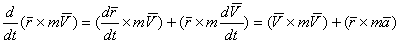 .
.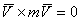 , как векторное произведение двух параллельных векторов, a
, как векторное произведение двух параллельных векторов, a  . Следовательно,
. Следовательно,
 .
. силы
силы 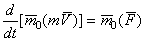 на эту ось. Математическое выражение теоремы моментов относительно оси дается формулой
на эту ось. Математическое выражение теоремы моментов относительно оси дается формулой  .
. . Под действием приложенных к ней внешних и внутренних сил
. Под действием приложенных к ней внешних и внутренних сил  и
и  (в которые входят и активные силы, и реакции связи) точка получает по отношению к инерционной системе отсчета некоторое ускорение
(в которые входят и активные силы, и реакции связи) точка получает по отношению к инерционной системе отсчета некоторое ускорение  .
. ,
, , то полученная система сил будет уравновешенной, т.е. будет
, то полученная система сил будет уравновешенной, т.е. будет .
. . Перенося здесь член
. Перенося здесь член 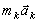 в правую часть равенства и придем к последнему соотношению.
в правую часть равенства и придем к последнему соотношению. . Силы же инерции, о которых говорится в принципе Даламбера, на движущиеся точки не действуют (иначе, эти точки находились бы в покое или двигались без ускорений и тогда не было бы и самих сил инерции). Введение сил инерции - это лишь приём, позволяющий составлять уравнения динамики с помощью более простых методов статики.
. Силы же инерции, о которых говорится в принципе Даламбера, на движущиеся точки не действуют (иначе, эти точки находились бы в покое или двигались без ускорений и тогда не было бы и самих сил инерции). Введение сил инерции - это лишь приём, позволяющий составлять уравнения динамики с помощью более простых методов статики.


 и
и  представляют собой главный вектор и главный момент относительно центра О системы сил инерции. В результате, учитывая, что геометрическая сумма внутренних сил и сумма их моментов равны нулю, получим из равенств:
представляют собой главный вектор и главный момент относительно центра О системы сил инерции. В результате, учитывая, что геометрическая сумма внутренних сил и сумма их моментов равны нулю, получим из равенств: ,
,  (1)
(1) , направленным в сторону перемещения.
, направленным в сторону перемещения. мы не считаем разными). Однако для каждой системы, в зависимости от характера наложенных на нее связей, можно указать определенное число таких независимых между собой перемещений, что всякое другое возможное перемещение будет получаться как геометрическая сумма. Например, шарик, лежащий на какой-нибудь плоскости (или поверхности), можно переместить вдоль этой плоскости по множеству направлений. Однако любое его возможное перемещение
мы не считаем разными). Однако для каждой системы, в зависимости от характера наложенных на нее связей, можно указать определенное число таких независимых между собой перемещений, что всякое другое возможное перемещение будет получаться как геометрическая сумма. Например, шарик, лежащий на какой-нибудь плоскости (или поверхности), можно переместить вдоль этой плоскости по множеству направлений. Однако любое его возможное перемещение  и
и 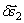 вдоль лежащих в этой плоскости взаимно перпендикулярных осей (
вдоль лежащих в этой плоскости взаимно перпендикулярных осей ( ).
). . И возможные перемещения точек его можно определить с помощью этого угла. Так, например,
. И возможные перемещения точек его можно определить с помощью этого угла. Так, например,  ;
; 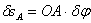 ;
; 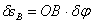 (рис.64, а и 64, б).
(рис.64, а и 64, б).
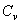 этого звена. А возможное перемещение всего тела при плоскопараллельном движении – есть поворот на малый угол
этого звена. А возможное перемещение всего тела при плоскопараллельном движении – есть поворот на малый угол  вокруг оси, проходящей через мгновенный центр скоростей. Этот угол можно определить.
вокруг оси, проходящей через мгновенный центр скоростей. Этот угол можно определить.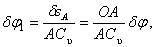 а перемещение ползуна В:
а перемещение ползуна В:  и точки С:
и точки С:  . То есть перемещения всех точек механизма можно определить через одно возможное перемещение, перемещение звена ОА, через угол
. То есть перемещения всех точек механизма можно определить через одно возможное перемещение, перемещение звена ОА, через угол  ,
,  ,
,  ,…,
,…,  .
.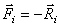 , то сумма работ этих сил на перемещении
, то сумма работ этих сил на перемещении 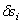 будет равна нулю:
будет равна нулю: 
 . Значит и сумма работ всех сил, приложенных ко всем точкам, будет равна нулю
. Значит и сумма работ всех сил, приложенных ко всем точкам, будет равна нулю .
.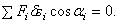 (1)
(1) где время
где время  - произвольная бесконечно малая величина, то уравнение работ (1) запишется так
- произвольная бесконечно малая величина, то уравнение работ (1) запишется так 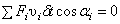 , а, поделив его на
, а, поделив его на  , (2)
, (2)


