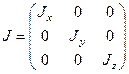Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Относительное движение материальной точкиСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Во многих задачах динамики движение материальной точки рассматривается относительно системы отсчета, движущейся относительно инерциальной системы отсчета.
где Согласно теореме Кориолиса Перепишем дифференциальное уравнение следующим образом
Введем обозначения
С учетом этих обозначений мы получаем динамическую теорему Кориолиса (уравнения относительного движения). Материальная точка движется относительно неинерциальной системы отсчета так же как и относительно инерциальной, только к приложенным активным силам и силам реакции связей следует добавить кориолисову и переносную силу инерции.
Силы В проекциях на подвижные оси
Частные случаи относительного движения 1. Относительное движение по инерции Если материальная точка движется относительно подвижной системы отсчета прямолинейно и равномерно, то такое движение называется относительным движением по инерции.
2. Относительное равновесие При покое материальной точки относительно подвижной системы отсчета ее относительные скорость и ускорение равны нулю, т.е.
Условие относительного равновесия имеет вид:
3. Инерциальные системы отсчета Переносное ускорение в общем случае вычисляется по формуле
где Если подвижная система отсчета движется поступательно, прямолинейно и равномерно, то
и уравнения относительного движения имеют вид:
Подвижная система отсчета тоже инерциальна.
Пример 1 Лифт движется вверх с ускорением
Пример 2
Лекция 5 Краткое содержание: Внутренние и внешние силы. Центр масс. Моменты инерции относительно точки и осей. Теорема Штейнера.
Введение в динамику системы Механической системой называется любая система материальных точек и тел. Внешними силами механической системы называются силы, с которыми на точки и тела механической системы действуют точки и тела не входящие в рассматриваемую систему. Равнодействующая всех внешних сил приложенных к Внутренними силами механической системы называются силы взаимодействия между точками и телами рассматриваемой системы. Равнодействующая всех внутренних сил приложенных к Это разделение является условным и зависит от того, какая механическая система рассматривается. Внутренние силы системы обладают следующими свойствами: Теорема. Главный вектор всех внутренних сил системы (векторная сумма) равен нулю при любом состоянии системы. Доказательство: Согласно одной из аксиом динамики, любые две точки системы действуют друг на друга с равными по величине, но противоположно направленными силами. Векторная сумма этих сил равна нулю. Все внутренние силы являются большим количеством таких парных сил. Поэтому сумма всех внутренних сил равна нулю.
Теорема. Главный момент всех внутренних сил системы (векторная сумма) относительно любой точки или оси равен нулю при любом состоянии системы. Доказательство: Любые две точки системы действуют друг на друга с равными по величине, но противоположно направленными силами. Сумма моментов этих сил относительно любой точки или оси равна нулю. Все внутренние силы являются большим количеством таких парных сил. Поэтому сумма моментов всех внутренних сил относительно любой точки или оси равна нулю.
Дифференциальные уравнения системы в векторной форме:
Геометрия масс Рассмотрим механическую систему, которая состоит из конечного числа
где Если механическая система представляет собой сплошное тело, то его разбивают на элементарные частицы с бесконечно малыми массами Центр масс является не материальной точкой, а геометрической. Центр масс характеризует распределение масс в системе. Координаты центра масс имеют вид:
Для тел типа тонкого листа (поверхность) и тонкой проволоки (линия)
Моменты инерции Для характеристики распределения масс в телах при рассмотрении вращательных движений требуется ввести понятия моментов инерции. Момент инерции относительно точки Скалярная величина
называется полярным моментом инерции относительно точки О. d – расстояние от текущей точки до точки О. Момент инерции относительно оси Скалярная величина называется моментом инерции относительно оси l. r – расстояние от точки до оси. Моменты инерции одинаковых по форме однородных тел, изготовленных из разных материалов, отличаются друг от друга. Характеристикой, не зависящей от массы материала, является радиус инерции. Величина Момент инерции относительно оси через радиус инерции относительно этой же оси определяется выражением Моменты инерции относительно осей координат
Центробежные моменты инерции
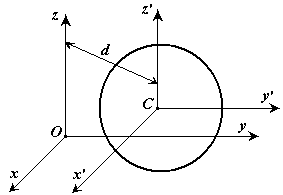
Установим зависимость между моментами инерции относительно параллельных осей, одна из которых проходит через центр масс. Теорема о моментах инерции относительно параллельных осей. (Теорема Штейнера) Момент инерции системы относительно какой-либо оси равен моменту инерции относительно параллельной оси, проходящей через центр масс, плюс произведение массы системы на квадрат расстояния между этими осями. Доказательство: Пусть имеется две декартовы системы координат
Координаты связаны между собой соотношениями:
Следовательно
Главными осями инерции называются оси, в которых центробежные моменты инерции равны нулю. Моменты инерции тела относительно главных осей инерции называются главными моментами инерции тела.
Тензор инерции и тензор инерции для главных осей:
|
|||||||
|
Последнее изменение этой страницы: 2016-06-28; просмотров: 421; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.148.105.127 (0.007 с.) |


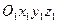 - инерциальная система отсчета.
- инерциальная система отсчета.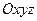 - подвижная система отсчета.
- подвижная система отсчета. ,
, - сумма активных сил,
- сумма активных сил, 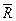 - сумма сил реакции связи.
- сумма сил реакции связи.
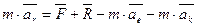
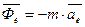 - переносная сила инерции,
- переносная сила инерции,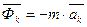 - кориолисова сила инерции.
- кориолисова сила инерции.
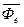 и
и 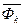 являются поправками на неинерционность системы.
являются поправками на неинерционность системы.
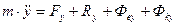
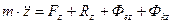
 ,
,  , следовательно
, следовательно
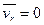 и
и 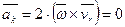

 ,
,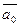 - ускорение точки, принятой за полюс (начало координат);
- ускорение точки, принятой за полюс (начало координат); 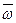 -угловая скорость вращения подвижной системы координат вокруг выбранного полюса;
-угловая скорость вращения подвижной системы координат вокруг выбранного полюса;  -угловое ускорение этого вращения (
-угловое ускорение этого вращения ( );
); 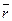 - радиус-вектор движения точки относительно полюса.
- радиус-вектор движения точки относительно полюса.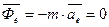 ,
, 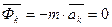
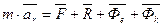 .
.
 точке обозначается
точке обозначается  (от латинского exterior - внешний).
(от латинского exterior - внешний).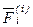 (от латинского interior - внутренний).
(от латинского interior - внутренний). .
.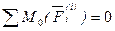 или
или 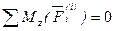 .
.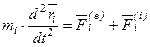 ,
, 
 материальных точек с массами
материальных точек с массами  , а положение точек в пространстве задается радиус-векторами
, а положение точек в пространстве задается радиус-векторами 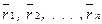 , то
, то Центром масс механической системы называется геометрическая точка С, радиус-вектор которой
Центром масс механической системы называется геометрическая точка С, радиус-вектор которой  определяется выражением
определяется выражением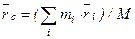
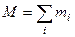 - масса системы.
- масса системы. . Суммы в пределе переходят в интегралы и центр масс определяется выражением
. Суммы в пределе переходят в интегралы и центр масс определяется выражением 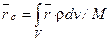
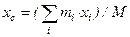
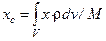
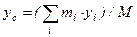


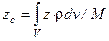
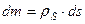 и
и 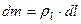 , где
, где 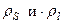 - поверхностная и линейная плотности соответственно. Интегралы вычисляются по поверхности и линии.
- поверхностная и линейная плотности соответственно. Интегралы вычисляются по поверхности и линии.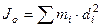 или
или 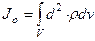
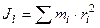 или
или 
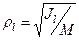 называется радиусом инерции.
называется радиусом инерции.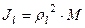 .
.
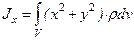
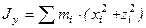
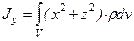
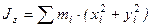
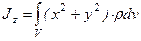
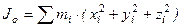
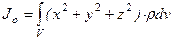



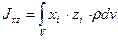
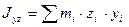

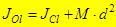
 , оси которых параллельны. Начало системы
, оси которых параллельны. Начало системы 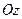 и
и 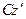 .
.
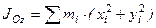
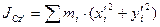
 ,
, 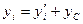 ,
, 

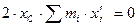 ,
,  ,
, 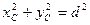 .
. , что и требовалось доказать.
, что и требовалось доказать.