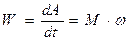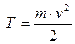Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Общие теоремы динамики точкиСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
Для решения многих задач динамики вместо непосредственного интегрирования дифференциальных уравнений движения оказывается более эффективным пользоваться так называемыми общими теоремами, которые являются следствием основного закона динамики. Количество движения точки Количеством движения материальной точки Количество движения точки в физике часто называют импульсом материальной точки. Проекции количества движения точки на прямоугольные декартовы оси координат равны:
Единицей измерения количества движения в СИ является –
Элементарный и полный импульс силы. Действие силы Полный импульс силы В частном случае, если сила Проекции импульса силы на прямоугольные декартовы оси координат равны:
Единицей измерения импульса в СИ является –
Теорема об изменении количества движения точки. Теорема. Производная по времени от количества движения точки равна действующей на точку силе. Запишем основной закон динамики Тогда что и требовалось доказать. В проекциях на координатные оси уравнение (*) можно представить в виде:
Теорема импульсов (в дифференциальной форме). Дифференциал от количества движения точки равен элементарному импульсу силы, действующей на точку. Умножим левую и правую части уравнения (*) на
В проекциях на координатные оси получаем:
Теорема импульсов (в интегральной форме). Изменение количества движения точки за какой-либо промежуток времени равно импульсу силы за этот же промежуток времени. Интегрируя обе части уравнения (**) по времени в пределах от нуля до
В проекциях на координатные оси получаем:
Момент количества движения точки. В некоторых задачах в качестве динамической характеристики движущейся точки вместо самого количества движения рассматривают его момент относительно какого-либо центра или оси. Эти моменты определяются также как и моменты силы.
Момент количества движения точки называют также кинетическим моментом. Момент количества движения относительно какой-либо оси Если количество движения
Единицей измерения количества движения в СИ является –
Теорема об изменении момента количества движения точки. Теорема. Производная по времени от момента количества движения точки, взятого относительно какого-нибудь центра, равна моменту действующей на точку силы относительно того же центра.
Доказательство: Продифференцируем момент количества движения по времени
что и требовалось доказать. Теорема. Производная по времени от момента количества движения точки, взятого относительно какой-либо оси, равна моменту действующей на точку силы относительно той же оси. Для доказательства достаточно спроектировать векторное уравнение (*) на эту ось. Для оси Следствия из теорем: 1. Если момент силы относительно точки равен нулю, то момент количества движения относительно этой точки величина постоянная.
2. Если момент силы относительно оси равен нулю, то момент количества движения относительно этой оси величина постоянная.
Работа силы. Мощность. Одна из основных характеристик силы, оценивающих действие силы на тело при некотором его перемещении.
Единицей измерения работы в СИ является – При Частные случаи:
Элементарное перемещение равно дифференциалу радиуса вектора точки приложения силы. Элементарная работа силы равна скалярному произведению силы на элементарное перемещение или на дифференциал радиуса вектора точки приложения силы.
Элементарная работа силы равна скалярному произведению элементарного импульса силы на скорость точки.
Если сила
Работа силы на любом конечном перемещении
Мощностью силы называется величина, определяющая работу, совершаемую силой в единицу времени. В общем случае мощность равна первой производной по времени от работы.
Мощность равна скалярному произведению силы на скорость. Единицей измерения мощности в СИ является – В технике за единицу силы принимается Пример 1. Работа силы тяжести.
Тогда,
Работа силы тяжести равна взятому со знаком плюс или минус произведению модуля силы на вертикальное перемещение точки ее приложения. Работа положительна, если начальная точка выше конечной, и отрицательна, если начальная точка ниже конечной.
Пример 2. Работа силы упругости.
Работа силы упругости равна половине произведения жесткости упругого элемента на разность квадратов начального и конечного удлинения (или сжатия) упругого элемента. Работа силы упругости равна площади фигуры (трапеции) расположенной под кривой
Пример 3. Работа и мощность пары сил.
Мощность пары сил равна
Кинетическая энергия точки Кинетической энергией материальной точки (или ее живой силой) называют половину произведения массы точки на квадрат ее скорости.
|
||||
|
Последнее изменение этой страницы: 2016-06-28; просмотров: 485; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.224.73.107 (0.007 с.) |

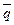 называется вектор, равный произведению массы точки
называется вектор, равный произведению массы точки  на ее скорость
на ее скорость 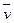 .
. 
 ,
, 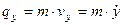 ,
, 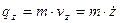
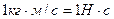
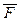 на материальную точку в течении времени
на материальную точку в течении времени 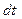 можно охарактеризовать элементарным импульсом силы
можно охарактеризовать элементарным импульсом силы 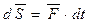 .
.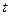 , или импульс силы
, или импульс силы 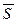 , определяется по формуле
, определяется по формуле 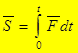 . (Полный интеграл за время
. (Полный интеграл за время 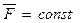 ),
), 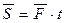 .
.
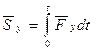
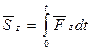

 в виде
в виде  . Так как масса постоянна, то внесем ее под знак производной.
. Так как масса постоянна, то внесем ее под знак производной. , (*)
, (*)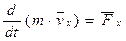
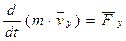
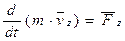
 (**)
(**)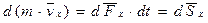 ,
, ,
, .
.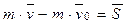
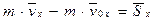 ,
,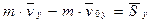 ,
,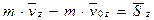
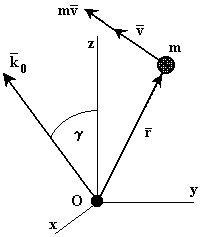 Моментом количеством движения материальной точки
Моментом количеством движения материальной точки 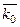 относительно некоторого центра О называется вектор, определяемый равенством
относительно некоторого центра О называется вектор, определяемый равенством 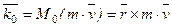
 , проходящий через центр О, равен проекции вектора количества движения
, проходящий через центр О, равен проекции вектора количества движения 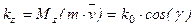 .
. задано своими проекциями
задано своими проекциями 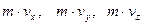 на оси координат и даны координаты
на оси координат и даны координаты 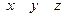 точки
точки 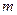 в пространстве, то момент количества движения
в пространстве, то момент количества движения 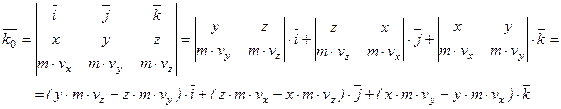 Проекции момента количества движения
Проекции момента количества движения 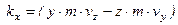
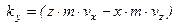

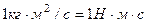 .
.

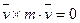 ,
,  , следовательно
, следовательно 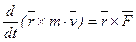 , (*)
, (*)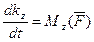
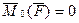 ,
, 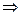
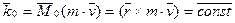
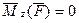 ,
, 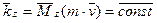
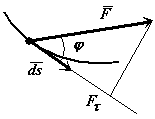 Элементарная работа силы скалярная величина равная произведению элементарного перемещения на проекцию силы на это перемещение.
Элементарная работа силы скалярная величина равная произведению элементарного перемещения на проекцию силы на это перемещение.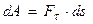 .
. 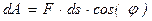 ,
,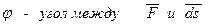
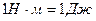
 при
при 
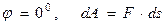
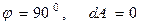
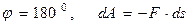
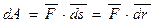

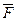 задана своими проекциями (
задана своими проекциями ( ) на оси координат и элементарное перемещение задано своими проекциями (
) на оси координат и элементарное перемещение задано своими проекциями (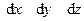 ) на оси координат, то элементарная работа силы равна:
) на оси координат, то элементарная работа силы равна: (аналитическое выражение элементарной работы).
(аналитическое выражение элементарной работы).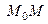 равна взятому вдоль этого перемещения интегралу от элементарной работы.
равна взятому вдоль этого перемещения интегралу от элементарной работы.
 ,
, 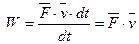

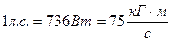 .
. Пусть точка М, на которую действует сила тяжести Р, перемещается из положения
Пусть точка М, на которую действует сила тяжести Р, перемещается из положения  в положение
в положение  . Выберем оси координат так, чтобы ось
. Выберем оси координат так, чтобы ось 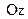 была направлена вертикально вверх.
была направлена вертикально вверх.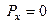 ,
, 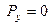 ,
, 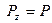 и
и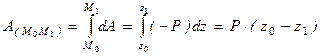
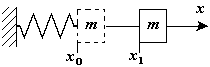 Рассмотрим материальную точку закрепленную на упругом элементе жесткости с, которая совершает колебания вдоль оси х. Сила упругости (или восстанавливающая сила)
Рассмотрим материальную точку закрепленную на упругом элементе жесткости с, которая совершает колебания вдоль оси х. Сила упругости (или восстанавливающая сила) 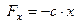 . Пусть точка М, на которую действует только сила упругости, перемещается из положения
. Пусть точка М, на которую действует только сила упругости, перемещается из положения 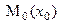 в положение
в положение 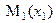 . (
. (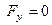 ,
, 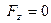 ).
).

 .
. 
 Пусть пара сил приложена к вращающемуся вокруг неподвижной оси телу. Элементарная работа пары сил равна
Пусть пара сил приложена к вращающемуся вокруг неподвижной оси телу. Элементарная работа пары сил равна  . Полная работа пары сил равна
. Полная работа пары сил равна 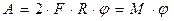
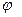 - угол поворота тела,
- угол поворота тела,  - момент пары сил.
- момент пары сил.