
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Динамика материальной точки и системы материальных точек. Законы сохранения.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
МЕХАНИКА Кинематика. Закон инерции. 1. Модели физических объектов. Условия их применения.
Простейшей моделью является материальная точка — тело, обладающее массой, размерами которо- го в данной задаче можно пренебречь. Материальная точка — понятие абст- рактное, но его введение облегчает ре- шение практических задач. Например, изучая движение планет но орбитам вокруг Солнца, можно принять их за материальные точки.
В механике вводится еще одна модель — абсолютно твердое тело. Абсолютно твердым называют тело, которое ни при каких условиях не может деформи- роваться и при всех условиях расстоя- ние между двумя точками (или точнее между двумя частицами) этого тела ос- тается постоянным.
2. Система отсчета. Декартова система координат. Траектория движения. Кинематическое описание движения материальной точки. Закон движения. Радиус-вектор. Вектор перемещения. Мгновенная скорость. Ускорение.
В декартовой системе координат,используемое наиболее часто,полоджение точки А в данный момент времени по отношению к этой системе характеризуется тремя координатами x,y,z Или радиусом – вектором r,проведенным из начала системы координат в данную точку.
Траектория – линия, описываемая в пространстве движущейся точкой. В зависимости от формы траектории движение может быть прямолинейным или криволинейным. Если мы будем определять радиус вектором r(t) то радиус вектор зависит от времени, эта зависимость называется ЗАКОНОМ ДВИЖЕНИЯ. Радиус вектор - вектор, задающий положения точки в пространстве относительно некоторой заранее фиксированной точки, называемой началом координат.
При неограниченном уменьшении At средняя скорость стремится к предельному значению, которое называется мгновенной скорость v Ускорение – физическая величина, характеризующая быстроту изменения скорости по модулю и направлению.
3. Движение материальной точки по окружности. Вектор углового перемещения, скорости, ускорения. Связь с линейными характеристиками движения. Нормальное, тангенциальное, полное ускорение при криволинейном движении. Равномерное движение МТ по окружности - движение материальной точки по окружности, при котором модуль ее скорости не меняется. При таком движении материальная точка обладает центростремительным ускорением.
В общем случае ускорение направлено под углом к скорости. Составляющая ускорения, направленная вдоль скорости, называется тангенциальным ускорением
Составляющая ускорения, направленная к центру кривизны траектории, т.е. перпендикулярно (нормально) скорости, называется нормальным ускорением Здесь R - радиус кривизны траектории в данной точке.
Тангенциальное и нормальное ускорение взаимноперпендикулярны, поэтому модуль полного ускорения
4. Закон инерции. Определение инерциальной системы отсчета. Принцип относительности Галилея. Преобразования координат. Следствия из преобразований Галилея. Закон сложения скоростей. Инвариантные величины. Закон инерции (1ый закон ньютона) - Существуют такие системы отсчёта, называемые инерциальными, относительно которых материальная точка при отсутствии внешних воздействий сохраняет величину и направление своей скорости неограниченно долго. Инвариантные величины - физическая величина, не меняющая своего числового значения при переходе из одной системы координат в другую. Закон сложения скоростей - определяет связь между значениями скорости материальной точки по отношению к разл.системам отсчёта, движущимся друг относительно друга. Определение момента импульса материальной точки и момента силы. Проекция векторов момента импульса и момента силы на выбранную ось Уравнение моментов для материальной точки. При каких условиях сохраняется момент импульса материальной точки? Момент силы — векторная физическая величина, равная произведению радиус-вектора, проведенного от оси вращения к точке приложения силы, на вектор этой силы. Характеризует вращательное действие силы на твёрдое тело. Моментом импульса материальной точки А относительно неподвижной точки О называется физическая величина, определяемая векторным произведением: L = [rp] = [r,mv], где г — радиус-вектор, проведенный из точки О в точку А; р = mv — импульс Вектор Условие сохранения - остается постоянной, пока на систему не воздействуют внешние силы 5. Система материальных точек. Вывод уравнения движения системы материальных точек на примере двух жестко связанных тел(хз) Системой материальных точек называется такая их совокупность, в которой положение и движение каждой точки зависит от положения и движения всех точек данной системы. Часто систему материальных точек называют механической системой. Центр масс системы материальных точек. Определение радиус-вектора центра масс. Свойства центра масс. Скорость центра масс. Вывод уравнения движения центра масс. Закон сохранения координаты центра масс системы материальных точек.
Цен- тром масс (или центром инерции) системы материальных точек называет- ся воображаемая точка С, положение которой характеризует распределение массы этой системы. Ее радиус-вектор равен
Центр масс замкнутой системы либо движется прямолинейно и равномерно, либо остается неподвижным.
Скорсть центра масс Для непрерывного распределения массы с плотностью r Подставляя это выражение в закон изменения полного импульса, находим: При поступательном движении все точки твердого тела движутся так же, как и центр масс (по таким же траекториям), поэтому для описания поступательного движения достаточно записать и решить уравнение движения центра масс. Так как
Rс(t1) = Rc(t2) закон сохранения координаты центра масс
8. Работа потенциальных (консервативных) силы на примере силы тяжести. Определение потенциальных (консервативных) силовых полей. Введение понятия потенциальной энергии через работу силы. Связь силы и потенциальной энергии
Потенциальная сила - сила, работа к-рой зависит только от начального и конечного положения точки её приложения и не зависит ни от вида траектории, ни от закона движения этой точки. Консервативные силы — такие силы, работа которых по любой замкнутой траектории равна 0.
Механика абсолютно твердого тела.
1 Модель абсолютно твердого тела (определение). Уравнение движения АТТ на примере двух жестко связанных материальных точек, вращающихся вокруг оси. Введение понятия момента инерции. В механике вводится еще одна модель — абсолютно твердое тело. Абсолютно твердым называют тело, которое ни при каких условиях не может деформи- роваться и при всех условиях расстоя- ние между двумя точками (или точнее между двумя частицами) этого тела ос- тается постоянным.
2 Применение момента инерции АТТ при вращательном движении. Его физический Механические колебания. 1 Определение гармонических свободных колебаний. Вывод уравнения колебаний на примере пружинного маятника. Круговая частота и период колебаний. Решение уравнения колебаний. 2 Гармонические свободные колебания в вязкой среде. Коэффициент сопротивления Неразрывности струи. 2 Понятия линии и трубки тока в жидкости. Вывод уравнения Бернулли из закона Пито - Прандтля. 4 Возникновение силы внутреннего трения в жидкостях и газах. Формула Ньютона МЕХАНИКА Кинематика. Закон инерции. 1. Модели физических объектов. Условия их применения.
Простейшей моделью является материальная точка — тело, обладающее массой, размерами которо- го в данной задаче можно пренебречь. Материальная точка — понятие абст- рактное, но его введение облегчает ре- шение практических задач. Например, изучая движение планет но орбитам вокруг Солнца, можно принять их за материальные точки.
В механике вводится еще одна модель — абсолютно твердое тело. Абсолютно твердым называют тело, которое ни при каких условиях не может деформи- роваться и при всех условиях расстоя- ние между двумя точками (или точнее между двумя частицами) этого тела ос- тается постоянным.
2. Система отсчета. Декартова система координат. Траектория движения. Кинематическое описание движения материальной точки. Закон движения. Радиус-вектор. Вектор перемещения. Мгновенная скорость. Ускорение.
В декартовой системе координат,используемое наиболее часто,полоджение точки А в данный момент времени по отношению к этой системе характеризуется тремя координатами x,y,z Или радиусом – вектором r,проведенным из начала системы координат в данную точку.
Траектория – линия, описываемая в пространстве движущейся точкой. В зависимости от формы траектории движение может быть прямолинейным или криволинейным. Если мы будем определять радиус вектором r(t) то радиус вектор зависит от времени, эта зависимость называется ЗАКОНОМ ДВИЖЕНИЯ. Радиус вектор - вектор, задающий положения точки в пространстве относительно некоторой заранее фиксированной точки, называемой началом координат.
При неограниченном уменьшении At средняя скорость стремится к предельному значению, которое называется мгновенной скорость v Ускорение – физическая величина, характеризующая быстроту изменения скорости по модулю и направлению.
3. Движение материальной точки по окружности. Вектор углового перемещения, скорости, ускорения. Связь с линейными характеристиками движения. Нормальное, тангенциальное, полное ускорение при криволинейном движении. Равномерное движение МТ по окружности - движение материальной точки по окружности, при котором модуль ее скорости не меняется. При таком движении материальная точка обладает центростремительным ускорением.
В общем случае ускорение направлено под углом к скорости. Составляющая ускорения, направленная вдоль скорости, называется тангенциальным ускорением
Составляющая ускорения, направленная к центру кривизны траектории, т.е. перпендикулярно (нормально) скорости, называется нормальным ускорением Здесь R - радиус кривизны траектории в данной точке.
Тангенциальное и нормальное ускорение взаимноперпендикулярны, поэтому модуль полного ускорения
4. Закон инерции. Определение инерциальной системы отсчета. Принцип относительности Галилея. Преобразования координат. Следствия из преобразований Галилея. Закон сложения скоростей. Инвариантные величины. Закон инерции (1ый закон ньютона) - Существуют такие системы отсчёта, называемые инерциальными, относительно которых материальная точка при отсутствии внешних воздействий сохраняет величину и направление своей скорости неограниченно долго. Инвариантные величины - физическая величина, не меняющая своего числового значения при переходе из одной системы координат в другую. Закон сложения скоростей - определяет связь между значениями скорости материальной точки по отношению к разл.системам отсчёта, движущимся друг относительно друга. Динамика материальной точки и системы материальных точек. Законы сохранения.
|
|||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 1092; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.102 (0.012 с.) |


 . Она характеризует изменение скорости по модулю.
. Она характеризует изменение скорости по модулю. 
 . Она характеризует изменение скорости по направлению.
. Она характеризует изменение скорости по направлению. 

 будет направлен вдоль нормали к плоскости, образованной векторами
будет направлен вдоль нормали к плоскости, образованной векторами  и
и  ,направление которого определяется по правилу буравчика.
,направление которого определяется по правилу буравчика.
 . Если силы тяжести, приложенные к каждой частице системы, направлены в одну сторону, то центр масс совпадает с центром тяжести. Но если
. Если силы тяжести, приложенные к каждой частице системы, направлены в одну сторону, то центр масс совпадает с центром тяжести. Но если  не параллельны, то центр масс и центр тяжести не совпадают.
не параллельны, то центр масс и центр тяжести не совпадают.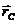 , получим:
, получим: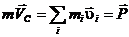

 , то центр масс замкнутой системы должен сохранять состояние покоя или равномерного прямолинейного движения, т.е.
, то центр масс замкнутой системы должен сохранять состояние покоя или равномерного прямолинейного движения, т.е.  =const. Но при этом вся система может вращаться, разлетаться, взрываться и т.п. в результате действия внутренних сил.
=const. Но при этом вся система может вращаться, разлетаться, взрываться и т.п. в результате действия внутренних сил.



