
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Понятие массы и импульса тела. Их свойства. Введение понятия силы как меры взаимодействия тел. Свойства сил. Принцип суперпозиции. Силы в механике.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Ма́сса - скалярная физическая величина, одна из важнейших величин в физике. Первоначально она характеризовала «количество вещества» в физическом объекте. Масса - это мера инертности тела. Масса аддитивна и инвариантна относительно смены системы отсчета И́мпульс (Количество движения) — векторная физическая величина, являющаяся мерой механического движения тела. В классической механике импульс тела равен произведению массы m этого тела на его скорость v, направление импульса совпадает с направлением вектора скорости:. может быть только положительной величиной, либо равной нулю. Сила - Сила - векторная величина, характеризующая механическое действие одного тела на другое, которое проявляется в деформациях рассматриваемого тела и изменении его движения относительно других тел.Сила характеризуется модулем и направлением. Модуль и направление силы не зависят от выбора системы отсчета. Способы измерения силы: динамометром. Единица измерения силы в СИ - 1 Н. Свойства силы: 1. Сила является функцией скорости и положения материальной точки. F= f((Vx;Vy;Vz), x, y, z). 2. Сила, с которой одна частица действует на другую зависит от R векторов и скоростей только этих двух частиц, присутствие других частиц на эту силу не влияет. Это свойство силы называют принципом парности взаимодействия. Следствие из него называется принципом суперпозиции. 3. 3-й закон Ньютона - сила действия равна силе противодействия При́нцип суперпози́ции — один из самых общих законов во многих разделах физики. В самой простой формулировке принцип суперпозиции гласит: “результат воздействия на частицу нескольких внешних сил есть векторная сумма воздействия этих сил” (Взаимодействие между двумя частицами не изменяется при внесении третьей частицы, также взаимодействующей с первыми двумя.) Силы в механике: 1) Сила тяготения, гравитационная.. 2) Сила упругости, электромагнитная.. 3)Сила трения, сухого, жидкого. электромагнитная.
Законы классической механики Ньютона. Условия применимости законов Ньютона. Основной закон классической динамики материальной точки. Решение основной задачи динамики.
Первый закон Ньютона: всякая материальная точка (тело) сохраняет состояние покоя или равномерного прямолинейного движения до тех пор, пока воздействие со стороны других тел не заставит ее изменить это состояние. Свойство тела сохранять свое состояние называется инертностью. Поэтому первый закон Ньютона называют законом инерции. Второй закон Ньютона: ускорение, приобретаемое материальной точкой или телом, пропорционально вызывающей его силе, совпадает с нею по направлению и обратно пропорционально массе материальной точки (тела). Третий закон Ньютона: Действие равно противодействию: F = -F. Условия применимости законов Ньютона: В инерциальных системах отсчета и при движении со скоростями, много меньшими скорости света. Основной закон классической динамики МТ - Масса движущихся релятивистских частиц зависит от их скорости:
где m0 — масса покоя частицы, т. е. масса, измеренная в той инерциальной системе отсчета, относительно которой частица находится в покое; с — скорость света в ваку уме; т — масса частицы в системе отсчета, относительно которой она движется со скоростью v. Следовательно, масса одной и той же частицы различна в разных инерциальных системах отсчета. Решение основной задачи динамики – 1) Зная массу точки и ее движение, найти силы, действующие на точку или их равнодействующую. 1. Составить дифференциальные уравнения 2. По известному движению материальной точки найти проекции ускорения на оси координат, которые выбраны для составления дифференциальных уравнений. 3. Подставляя проекции ускорения в составленные дифференциальные уравнения, найти проекции равнодействующей сил, приложенных к точке. 4. Используя дополнительные условия, например, направления реакций связей, определить по равнодействующей силы, приложенные к точке. Если на точку действует одна сила, то для нахождения величины и направления этой силы можно использовать формулы (1) - (3), полученные для равнодействующей. 5. Проанализировать полученное решение.
2) Зная приложенные к точке силы, а также ее массу, определить ее движение, описываемое кинематическими уравнениями. 1. Составить дифференциальные уравнения для конкретного случая движения материальной точки 2. Определить и записать начальные условия задачи. 3. Проинтегрировать дифференциальные уравнения в соответствии с методами, известными из курса математики, определяя постоянные интегрирования с помощью начальных условий, для нахождения единственногорешения. 4. Проанализировать полученный в решении закон движения материальной точки в зависимости от конкретных вопросов в задаче и найти ответы на них. 5.системой материальных точек называется такая их совокупность,в которой положение и движение каждой точки зависит от положения и движения всех точек данной системы.
Какие взаимодействия относятся к фундаментальным? На каких расстояниях проявляются фундаментальные взаимодействия? Какова относительная интенсивность фундаментальных взаимодействий? Фундаментальные воздействия 1)слабое (менее 10-15) интнесивность – 10-13 2)сильное (менее 10-15) интнесивность – 1 3) Электростатическое (от 0 до беконеч.) интнесивность – 10-2 4) Гравитационное (от 0 до беконеч.) интнесивность – 10-38
Определение момента импульса материальной точки и момента силы. Проекция векторов момента импульса и момента силы на выбранную ось Уравнение моментов для материальной точки. При каких условиях сохраняется момент импульса материальной точки? Момент силы — векторная физическая величина, равная произведению радиус-вектора, проведенного от оси вращения к точке приложения силы, на вектор этой силы. Характеризует вращательное действие силы на твёрдое тело. Моментом импульса материальной точки А относительно неподвижной точки О называется физическая величина, определяемая векторным произведением: L = [rp] = [r,mv], где г — радиус-вектор, проведенный из точки О в точку А; р = mv — импульс Вектор Условие сохранения - остается постоянной, пока на систему не воздействуют внешние силы 5. Система материальных точек. Вывод уравнения движения системы материальных точек на примере двух жестко связанных тел(хз) Системой материальных точек называется такая их совокупность, в которой положение и движение каждой точки зависит от положения и движения всех точек данной системы. Часто систему материальных точек называют механической системой. Центр масс системы материальных точек. Определение радиус-вектора центра масс. Свойства центра масс. Скорость центра масс. Вывод уравнения движения центра масс. Закон сохранения координаты центра масс системы материальных точек.
Цен- тром масс (или центром инерции) системы материальных точек называет- ся воображаемая точка С, положение которой характеризует распределение массы этой системы. Ее радиус-вектор равен
Центр масс замкнутой системы либо движется прямолинейно и равномерно, либо остается неподвижным.
Скорсть центра масс Для непрерывного распределения массы с плотностью r Подставляя это выражение в закон изменения полного импульса, находим: При поступательном движении все точки твердого тела движутся так же, как и центр масс (по таким же траекториям), поэтому для описания поступательного движения достаточно записать и решить уравнение движения центра масс. Так как
Rс(t1) = Rc(t2) закон сохранения координаты центра масс
8. Работа потенциальных (консервативных) силы на примере силы тяжести. Определение потенциальных (консервативных) силовых полей. Введение понятия потенциальной энергии через работу силы. Связь силы и потенциальной энергии
Потенциальная сила - сила, работа к-рой зависит только от начального и конечного положения точки её приложения и не зависит ни от вида траектории, ни от закона движения этой точки. Консервативные силы — такие силы, работа которых по любой замкнутой траектории равна 0.
Механика абсолютно твердого тела.
1 Модель абсолютно твердого тела (определение). Уравнение движения АТТ на примере двух жестко связанных материальных точек, вращающихся вокруг оси. Введение понятия момента инерции. В механике вводится еще одна модель — абсолютно твердое тело. Абсолютно твердым называют тело, которое ни при каких условиях не может деформи- роваться и при всех условиях расстоя- ние между двумя точками (или точнее между двумя частицами) этого тела ос- тается постоянным.
2 Применение момента инерции АТТ при вращательном движении. Его физический
|
||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 2865; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.01 с.) |

 будет направлен вдоль нормали к плоскости, образованной векторами
будет направлен вдоль нормали к плоскости, образованной векторами  и
и  ,направление которого определяется по правилу буравчика.
,направление которого определяется по правилу буравчика.
 . Если силы тяжести, приложенные к каждой частице системы, направлены в одну сторону, то центр масс совпадает с центром тяжести. Но если
. Если силы тяжести, приложенные к каждой частице системы, направлены в одну сторону, то центр масс совпадает с центром тяжести. Но если  не параллельны, то центр масс и центр тяжести не совпадают.
не параллельны, то центр масс и центр тяжести не совпадают.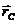 , получим:
, получим: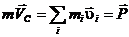

 , то центр масс замкнутой системы должен сохранять состояние покоя или равномерного прямолинейного движения, т.е.
, то центр масс замкнутой системы должен сохранять состояние покоя или равномерного прямолинейного движения, т.е.  =const. Но при этом вся система может вращаться, разлетаться, взрываться и т.п. в результате действия внутренних сил.
=const. Но при этом вся система может вращаться, разлетаться, взрываться и т.п. в результате действия внутренних сил.



