
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Принцип генерации ультракоротких импульсов: синхронизация модСодержание книги
Поиск на нашем сайте
До сих пор при описании лазеров мы не обращали внимания на различия между обычными лазерами и пикосекундными лазерами; не был также рассмотрен механизм, ответственный за формирование в лазере ультракоротких световых импульсов. В данном и следующем разделах мы коротко обсудим общий принцип такой генерации. Возникновение ультракоротких световых импульсов в лазерном резонаторе связано с тем уже упоминавшимся фактом, что в лазерных веществах с относительно большой шириной линии лазерного перехода может одновременно возбуждаться очень много собственных колебаний. Полная напряженность поля Е (t) лазерного излучения является результатом наложения напряженностей полей М отдельных аксиальных собственных колебаний:
где индекс суммирования m пробегает значения от m = -(М-1)/2 до m=(М-1)/2, a δν=δω/2π=c/2L — частотное расстояние между модами; здесь оно принято постоянным во всей области частот генерации. Это, например, соблюдается всегда, когда можно пренебречь дисперсией оптической среды, влияющей на оптическую длину резонатора L. В зависимости от свойств активного вещества и резонатора фазы φm различных собственных колебаний могут быть статистически зависимыми или статистически независимыми. Сначала рассмотрим случай статистической независимости (этот случай реализуется, если для отдельных мод существуют независимые источники энергии, например, при переходах с сильным неоднородным уширением). Для полной интенсивности имеем
Следовательно, в случае статистической независимости фаз φm полная интенсивность может быть представлена в виде суммы интенсивностей отдельных мод. На рис. 3.1 показана временная структура такого многомодового излучения внутри лазерного резонатора. В частотном представлении излучение состоит из большого числа дискретных спектральных линий, частотное расстояние между которыми равно c/2L. Каждая мода осциллирует независимо от других, и фазы распределены стохастически в интервале от -π до π. Во временном представлении поле характеризуется распределением интенсивностей, обладающим характеристическими свойствами гауссова шума.
Если же удается с помощью соответствующего механизма установить между отдельными собственными колебаниями фиксированное соотношение фаз, то возникает ситуация, качественно отличающаяся от описанной выше, что представляет очень большой интерес. Выходное излучение в этом случае определенным образом зависит от времени. Такой лазер называют лазером с синхронизацией мод или со связью между модами (захватом мод).
Качественное пояснение принципа действия лазера с синхролизацией мод можно дать при помощи следующего элементарного рассуждения. Предположим, что М мод обладают приблизительно одинаковыми амплитудами Е0, а их фазы удовлетворяют условию синхронизма
φm - φm-1 = α =const (3.3)
Тогда в (2.22) можно φm заменить на (m α + φ0)- Суммирование может быть выполнено аналитически, и мы приходим к соотношению
На рис. 3.2 показана зависимость выходного излучения от времени для М = 7. Вследствие определенного соотношения между фазами моды в резонаторе интерферируют, и поэтому лазерное излучение имеет форму коротких световых импульсов. Максимумы импульсов образуются в такие моменты времени, для которых знаменатель в 3.2 обращается в нуль, т. е. при условии (δωt+α)/2 = qn (q — целое число). Понятие синхронизации мод заключается в том, что в моменты времени tq все моды вносят максимальный вклад в суммарную напряженность поля. Интервал времени и между двумя соседними максимумами определяется выражением
u = 2π/δω = 2L/c (3.5)
Это именно то время, которое необходимо для полного прохода по резонатору. Следовательно, в резонаторе находится только один импульс, постоянно распространяющийся вперед и назад. Длительность импульса τL можно оценить также из (3.4):
τL = 2π/Mδω = 2π/ Δωген (3.6)
где Δωген есть частотный интервал, в котором заключены лазерные моды. При интенсивной накачке Δωген может принять значение, почти равное ширине линии лазерного перехода Δω21. Следовательно, могут быть получены тем более короткие импульсы, чем больше спектральная ширина линии лазерного перехода и чем больше число мод, превосходящих порог генерации. Обратное значение ширины линии определяет нижнюю границу длительности импульса, которая не должна существенно нарушаться. Ясно, что от типичных газовых лазеров низкого давления невозможно получить импульсы длительностью лорядка пикосекунд. Напротив, у твердотельных лазеров предельное значение длительности импульса имеет порядок величины 1 пс, а у лазеров на красителях эта величина еще на порядок ниже.
Помимо свойства очень малых длительностей лазерные импульсы с коррелированными фазами могут обладать еще очень высокими пиковыми интенсивностями. Согласно (3.4), максимальная интенсивность пропорциональна Свойства ультракоротких импульсов описываются соотношением (3.4) только в сильно идеализированной форме. В более общем виде временная структура оптического импульса полностью определяется модулем напряженности поля |EL(t)| или интенсивностью IL(t) и фазой φL(t). В общем случае измеряются контур интенсивности IL (t) и в частотном представлении спектральное распределение IL(ω), причем между этими двумя величинами не существует однозначной связи вследствие зависимости напряженности поля от фазы φL(t). Можно привести только соотношение между полуширинами τL и ΔνL обоих контуров в виде
ΔνL· τL ≥ CB, (3.7)
где СB есть численный множитель порядка единицы, величина которого определяется конкретной формой импульса. Самый короткий импульс, который может быть получен при заданной спектральной полуширине ΔνL·, называется импульсом, ограниченным шириной полосы, и его длительность равна τL = CB/ ΔνL.
Рассмотрим, например, общий гауссов импульс с медленно меняющейся во времени амплитудой напряженности поля
Е (t) = Е0 ехр (—γt2 + i βt2). (3.8)
Постоянная γ описывает в данном случае огибающую импульса и связана с полушириной мощности импульса соотношением
τL=(2 ln (2)/γ)1/2 (3.9)
Член i βt2 описывает линейное изменение частоты внутри импульса или фазовую модуляцию (рис. 3.3), которая в реальных условиях может возникнуть, например, вследствие дисперсии среды. Выполняя преобразование Фурье, получим из (2.29) для полуширины спектрального распределения интенсивности IL(ω)
Произведение ширины импульса на ширину полосы в данном случае определяется формулой
В частном случае β=0 (отсутствие фазовой модуляции) получаем СВ = 0,441. Из (2.32) следует, что при быстрой фазовой модуляции произведение длительности импульса на ширину полосы в (3.7) при β/γ>>1 может быть значительно больше единицы. Иногда для описания формы импульса лазера на красителе с синхронизацией мод применяется функция в виде гиперболического секанса (ch l,76t/ τL)-2. Для импульса такой формы постоянная СB принимает значение 0,315.
Для экспериментального использования эффекта синхронизации мод возникает задача: создать генерацию на максимальном числе собственных колебаний с постоянной разностью фаз в лазерно активной среде с широкой спектральной линией усиления. Для этой цели могут использоваться различные методы. Перечислим важнейшие методы и дадим их краткую характеристику.
Активная синхронизация мод
Метод активной синхронизации мод с помощью периодической модуляции параметров резонатора заключается в следующем. Внутри резонатора помещается модулятор, управляемый внешним сигналом и изменяющий потери резонатора (или другие его важные параметры, например оптическую длину пути) с течением времени по периодическому закону и с определенной частотой модуляции. Если частоту модуляции выбрать так, чтобы она равнялась частотному интервалу между модами для отдельных аксиальных мод, то вследствие модуляции для каждой моды начнется генерация побочных полос. Их частота будет совпадать с частотами обеих соседних мод. В результате этого эффекта между модами возникнет взаимодействие и при достаточно сильной модуляции все моды окажутся синхронизованными. Для активной синхронизации мод чаще всего применяются акустооптические или электрооптические модуляторы.
|
|||||||||||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 755; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.12.133 (0.01 с.) |

 +к.с. (3.1)
+к.с. (3.1) ~
~ 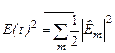 (3.2)
(3.2)

 +к.с. (3.4)
+к.с. (3.4)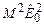 , тогда как в случае лазера с несинхронизованными модами, согласно (3.1), пиковая интенсивность пропорциональна
, тогда как в случае лазера с несинхронизованными модами, согласно (3.1), пиковая интенсивность пропорциональна 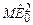 . Мы приходим к выводу, что при одном и том же числе мод интенсивность в максимуме в случае коррелированных фаз в М раз больше, чем при генерации лазерного излучения со случайным соотношением фаз между отдельными модами.
. Мы приходим к выводу, что при одном и том же числе мод интенсивность в максимуме в случае коррелированных фаз в М раз больше, чем при генерации лазерного излучения со случайным соотношением фаз между отдельными модами.
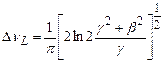 (3.10)
(3.10)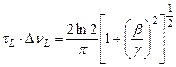 (3.11)
(3.11)


