
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Момент импульса. Закон сохранения момента импульсаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Моментом импульса материальной точки относительно некоторой точки О называется вектор
Модуль момента импульса
Направление момента импульса определяется по правилу правого винта (вектора Момент импульса системы материальных точек равен векторной сумме моментов импульсов отдельных материальных точек системы или векторному произведению радиус-вектора центра масс системы на импульс ее центра масс
Величина момента импульса твердого тела относительно оси вращения
где Изотропность пространства (осевая симметрия пространства) приводит к закону сохранения момента импульса: в замкнутых системах момент импульса сохраняется. В незамкнутых системах закон сохранения момент импульса выполняется в следующих случаях: 1 Если суммарный момент внешних сил равен нулю, то момент импульса системы сохраняется. 2 Если существует ось Z такая, что сумма проекций моментов внешних сил на эту ось равна нулю, то сохраняется проекция момента импульса системы на эту ось. 3 Момент импульса системы сохраняется, если время действия внешних сил мало. Закон сохранения момента импульса является фундаментальным законом природы, выполняющимся при любых взаимодействиях в мега-, макро- и микромире. Законом сохранения момента импульса объясняются, в частности, плоская форма галактик, орбитальное движение планет Солнечной системы (второй закон Кеплера), изменение угловой скорости вращения фигуриста при изменении положения его рук и т.д. Многие элементарные частицы обладают внутренним моментом импульса (спином). Суммарный спин системы взаимодействующих частиц сохраняется при любых процессах слабого и сильного взаимодействий.
Работа, мощность, энергия Изменение механического движения тела вызывается силами, действующими на него со стороны других тел. Чтобы количественно характеризовать процесс обмена энергией между взаимодействующими телами, в механике вводится понятие работы силы.
Механическая работа – это скалярная величина, равная скалярному произведению вектора силы на вектор перемещения точки Работа переменной силы на пути S
В частном случае постоянной силы, действующей под неизменным углом a к перемещению,
В системе СИ работа измеряется в джоулях (Дж). Работа может быть положительной (α < π/2) и отрицательной (α > π/2). Работа силы, перпендикулярной перемещению (например, силы притяжения Земли к Солнцу), равна нулю. Мощностью называется величина, определяемая работой, совершаемой в единицу времени:
(2.3.8)
В случае постоянной мощности
N = А/t, (2.3.9)
где А - работа, совершаемая за время t. В системе СИ мощность измеряется в ваттах (Вт). Энергия – это единая количественная мера различных форм движения и взаимодействия всех видов материи. Под движением в широком смысле слова понимают любое изменение материи. Различным формам движения соответствуют разные формы энергии: механическая, тепловая, электромагнитная, ядерная и т.д. Внутренней (тепловой) энергией называется сумма кинетической энергии теплового движения атомов и молекул тела и потенциальной энергии их взаимодействия. Электромагнитное поле является носителем электромагнитной энергии. Частным видом электромагнитной энергии является энергия электрического тока, широко используемая человеком. Ядерная энергия связана с взаимодействием протонов и нейтронов в ядре и может высвобождаться, например, при реакциях деления тяжелых ядер или при синтезе легких. Механическая энергия – энергия тел при их механическом движении. Она характеризует способность тела совершать механическую работу. Механическая энергия подразделяется на кинетическую (Т .) и потенциальную (П .). Полная механическая энергия тела Е м складывается из кинетической и потенциальной энергии
Е м= Т + П (2.3.10) Кинетическая энергия – это энергия, которой обладает движущееся тело. Кинетическая энергия тела, движущегося поступательно со скоростью V
Кинетическая энергия зависит от системы отсчета и в этом смысле является относительной величиной. Так, сидящий человек массой 60 кг не имеет кинетической энергии в СО, связанной с земной поверхностью, но в системе отсчета, связанной с Солнцем, обладает кинетической энергией Т ≈33 МДж.
Кинетическая энергия системы материальных точек равна сумме кинетических энергией отдельных точек системы. Кинетическая энергия тела с моментом инерции I, вращающегося вокруг неподвижной оси с угловой скоростью ω, определяется по формуле:
В общем случае тело может участвовать как в поступательном, так и во вращательном движении (колесо велосипеда). Тогда кинетическая энергия этого тела складывается из кинетической энергии поступательного движения и кинетической энергии вращения. Потенциальная энергия – часть механической энергии системы, связанная с взаимным расположением частей системы и определяемая характером сил, действующих между ними. Для каждого вида взаимодействия существует своя формула потенциальной энергии. Потенциальной энергией обладает тело, поднятое над поверхностью Земли, деформированная пружина и т.д. Потенциальная энергия тела массы m, поднятого на высоту h над поверхностью Земли, находится по формуле
П = mgh, (2.3.13)
где g – ускорение свободного падения. Потенциальная энергия упруго деформированного тела рассчитывается по формуле
где x – величина деформации, k – коэффициент упругости. Среди возможных состояний системы особое значение имеет состояние устойчивого равновесия – состояние, которое не изменяется при малом внешнем воздействии на систему. В состоянии устойчивого равновесия потенциальная энергия системы минимальна, многие явления природы объясняются стремлением потенциальной энергии к минимуму. Так, шарообразность массивных небесных тел (звезд, планет) объясняется тем, что этой формой достигается минимум потенциальной гравитационной энергии взаимодействия частиц этих тел. Закон сохранения энергии Однородность времени (сдвиговая симметрия) приводит к закону сохранения энергии: при любых процессах полная энергия изолированной системы не изменяется; энергия может только превращаться из одного вида в другой и передаваться от одного тела системы к другому. Закон сохранения энергии – фундаментальный закон природы, выполняющийся на всех структурных уровнях организации материи. Не существует явлений и процессов, для которых этот закон не имел бы места. Нарушение закона сохранения энергии свидетельствовало бы о нарушении однородности времени. Все явления и процессы в природе – от самых простых до самых сложных – протекают с сохранением энергии. Общий запас энергии во Вселенной с момента ее образования до наших дней остается постоянным. Появление высокоупорядоченных структур (от атомов и молекул до звезд и галактик) и явление жизни связано с последовательными превращениями одних форм энергии в другие. Часть энергии обязательно переходит в самую низшую форму – теплоту. Большое значение для практической деятельности человека имеет частный случай − закон сохранения механической энергии, выполняющийся в поле консервативных сил. Консервативной называется сила, работа которой не зависит от траектории, а определяется начальным и конечным состояниями системы. Работа консервативной силы по замкнутой траектории равна нулю. Консервативными являются сила тяжести, упругости, сила взаимодействия электрических зарядов и др. Сила, работа которой зависит от траектории перемещения тела из одной точки в другую, называется диссипативной. Примером диссипативной силы является сила трения; работа силы трения по любой замкнутой траектории меньше нуля. Силовые поля, в которых действуют консервативные силы (например, поле гравитационных или поле упругих сил), называются потенциальными.
Закон сохранения механической энергии: в системе тел, между которыми действуют только консервативные силы, полная механическая энергия сохраняется (не изменяется со временем) Е м= Т + П =const. (2.3.15)
В консервативных системах происходят превращения кинетической энергии в потенциальную и наоборот, при этом полная механическая энергия остается постоянной. В диссипативных системах механическая энергия постепенно уменьшается за счет преобразования в другие (немеханические) формы. Этот процесс называется диссипацией (или рассеянием) энергии. Так, если в механической системе есть сила трения, то механическая энергия частично превращается в тепловую.
Контрольные вопросы 1 Что такое симметрия? Приведите примеры операций симметрии. 2 Сформулируйте теорему Нетер. Какова связь между симметрией и законами сохранения? 3 Сформулируйте закон сохранения импульса. С каким свойством пространства связан этот закон? 4 Приведите примеры явлений, объясняющихся законом сохранения импульса. 5 Сформулируйте закон сохранения момента импульса. С каким свойством пространства связан этот закон? 6 Приведите примеры явлений, объясняющихся законом сохранения момента импульса. 7 Дайте определения энергии, мощности и работы. В чем заключается различие между понятиями энергии и работы? 8 Сформулируйте закон сохранения энергии. С каким свойством времени он связан? 9 В чем заключается закон сохранения механической энергии? В каких системах выполняется этот закон? 10 Какие силы называются консервативными? Диссипативными? Приведите примеры консервативных и диссипативных сил.
|
|||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 1558; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.133.149.244 (0.01 с.) |

 , равный векторному произведению радиус-вектора материальной точки относительно точки О на импульс материальной точки
, равный векторному произведению радиус-вектора материальной точки относительно точки О на импульс материальной точки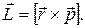 (2.3.2)
(2.3.2) (2.3.3)
(2.3.3)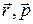 и
и  составляют правую тройку векторов).
составляют правую тройку векторов). (2.3.4)
(2.3.4) (2.3.5)
(2.3.5)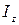 - момент инерции тела относительно оси z, w - угловая скорость тела.
- момент инерции тела относительно оси z, w - угловая скорость тела. (2.3.6)
(2.3.6) (2.3.7)
(2.3.7)
 (2.3.11)
(2.3.11) (2.3.12)
(2.3.12)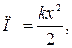 (2.3.14)
(2.3.14)


