
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Инерции кольца и момента силы трения в опоре.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
и расходуется на работу Определим теперь работу сил трения. Поскольку при вращении махового колеса его потенциальная энергия не изменяется, то работа всех внешних сил, которые действуют на него, равняется только увеличению кинетической энергии. Таким образом, элементарная работа сил трения при повороте махового колеса на бесконечно малый угол
Соответственно основному уравнению динамики вращательного движения тела вокруг недвижимой оси
Подставив это выражение в последнее уравнение для
где
Поскольку сила трения является внешней силой, а ее момент постоянный
Здесь После того как груз опустится на полную длину нити
Эта формула разрешает вычислить момент сил трения, если измерить радиус вала Применим теперь динамический метод к изучению движения махового колеса и получим выражение для расчета момента инерции кольца по экспериментальным данным. Уравнение движения системы в проекциях на оси Х и В имеют вид
Общее решение уравнений (6) и (7) дает
Полученное выражение разрешает рассчитать момент инерции всей системы относительно оси вращения Для определения момента инерции кольца необходимо воспользоваться тем обстоятельством, что момент инерции есть адитивна физическая величина. Если снять кольцо и провести такую же серию опытов по определению времени
Тогда момент инерции кольца
Порядок выполнения работы. 1. Измерить штангенциркулем диаметр вала (1) в разных его точках и определить среднее значение радиуса вала. 2. Поднять груз 3. Забрать подкладку, дав возможность груза 4. Снять кольцо (3) (см. рис. 3.) и повторить серию экспериментов по определению времени 5. Експериментальні даны занести в таблицу и вычислить средние значения измеренных величин. Таблица.
6. По среднему значению измеренных величин вычислить момент силы трения и момент инерции кольца, используя выражения (6) и (10). Определить момент инерции кольца без учета сил трения и сравнить результаты. 7. Измерив внутренний и внешний диаметр кольца, рассчитать его момент инерции (2') и уравнять с экспериментально полученным (10). 8. Определить погрешности прямых и косвенных измерений.
Контрольные вопросы: 1. Что называется моментом инерции? Какую роль играет момент инерции в динамике вращательного движения? Найдите путем интегрирования момент инерции тела правильной геометрической формы - пустого цилиндра. 2. Дайте определение момента силы. Чему равняется величина момента силы? Как направленный этот вектор? Момент какой силы сообщает маховому колесу угловое ускорение? Как направленный момент этой силы? Что такое момент импульса тела? Как направленный момент импульса? 3. Запишите основное уравнение динамики вращательного движения относительно данной задачи. 4. Изменяется ли направление момента силы, угловой скорости, момента импульса, углового ускорения, если нить начнет наматываться на вал, и тягарець будет подниматься вверх? 5. Выведите расчетную формулу для момента инерции махового колеса. Какие законы при этом употребятся? 6. При каком условии ускорения тягарця равняется тангенциальному ускорению точек на поверхности вала, из которого сматывается нить? 7. Чему при сравнимые значения моменте инерции махового колеса, полученного исследовательским путем, со значением, рассчитанным по формуле Литература: Методические указания. А.Н. Матвеев. Механика и теория относительности, -М., 1976, §22, 23, 48-50. Д.В. Сивухін. Общий курс физики, т. I, -М., 1974, §3, 4, 30, 32, 33, 36.53. С.Э.Хайкін. Физические основы механики, -М., 1971, § 11, 13, 14, 67, 68, 89. С.П. Стрелков. Механика, -М., 1975, §52, 53, 54, 53, 63-65.
Лабораторная работа №9
|
||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 859; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.108 (0.007 с.) |

 Экспериментальная установка (рис. 3) представляет собой вал (1) с диском (2), на котором крепится кольцо (3). Вал установленный на шарикоподшипниках и может вращаться. На вал радиуса
Экспериментальная установка (рис. 3) представляет собой вал (1) с диском (2), на котором крепится кольцо (3). Вал установленный на шарикоподшипниках и может вращаться. На вал радиуса 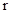 наматывается тонкая нить, длиной
наматывается тонкая нить, длиной  , до конца которой прикрепленный груз массой
, до конца которой прикрепленный груз массой  . Под действием силы тяготения
. Под действием силы тяготения  вся система начинает вращаться. Рассмотрим движение системы с точки зрения закона сохранения энергии. При движении груза из высоты
вся система начинает вращаться. Рассмотрим движение системы с точки зрения закона сохранения энергии. При движении груза из высоты  переходит в кинетическую энергию системы
переходит в кинетическую энергию системы (3)
(3) против сил трения в подшипниках. Кинетическая энергия системы представляет собой сумму кинетической энергии поступательного движения груза и кинетической энергии вращательного движения диска, кольца и вала. В силу аддитивности момента инерции, под
против сил трения в подшипниках. Кинетическая энергия системы представляет собой сумму кинетической энергии поступательного движения груза и кинетической энергии вращательного движения диска, кольца и вала. В силу аддитивности момента инерции, под  в выражении (3) понимается суммарный момент инерции кольца, диска и вала. Тогда при движении груза вниз до полного разматыванию нити на длину
в выражении (3) понимается суммарный момент инерции кольца, диска и вала. Тогда при движении груза вниз до полного разматыванию нити на длину  .
. :
: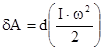 или
или  .
.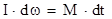 .
. и учтя, что
и учтя, что  , получим
, получим ,
, - угловое перемещение. Работа внешних сил при повороте твердого тела на конечный угол определится как
- угловое перемещение. Работа внешних сил при повороте твердого тела на конечный угол определится как .
.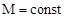 , то работа силы трения будет
, то работа силы трения будет 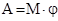 , здесь
, здесь  , где
, где  - число оборотов колеса. Тогда закон сохранения энергии при движении рассмотренной системы будет иметь вид
- число оборотов колеса. Тогда закон сохранения энергии при движении рассмотренной системы будет иметь вид (4)
(4) - момент сил трения, j - полный угол поворота колеса.
- момент сил трения, j - полный угол поворота колеса. , наверное,
, наверное,
 (5)
(5) - полный угол поворота колеса при подъеме груза. Учитывая, что
- полный угол поворота колеса при подъеме груза. Учитывая, что  , а
, а  из равенств (4) и (5) получаем
из равенств (4) и (5) получаем (6)
(6)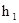 .
.
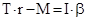 (7)
(7)
 (8)
(8) , если определить экспериментально время движения груза
, если определить экспериментально время движения груза 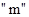 из высоты
из высоты  , движения груза из высоты
, движения груза из высоты  (9)
(9)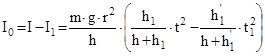 (10)
(10)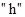 , наматывая нить на вал и зафиксировать его подкладкой.
, наматывая нить на вал и зафиксировать его подкладкой. к полному его опусканию на длину нити. Одновременно измерить высоту подъема груза при его движении вверх. Провести не менее 5 измерений
к полному его опусканию на длину нити. Одновременно измерить высоту подъема груза при его движении вверх. Провести не менее 5 измерений  .
. соответственно пункту 3.
соответственно пункту 3. , наблюдается расхождение? Как уменьшить это расхождение?
, наблюдается расхождение? Как уменьшить это расхождение?


