
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Момент силы относительной осиСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Момент силы относительной оси Моментом силы относительно оси называют алгебраический момент проекции этой силы на плоскость, перпендикулярную оси, относительно точки пересечения плоскостью. Момент силы относительно оси считается положительным, если проекция силы на плоскость, перпендикулярно оси (проекция силы на плоскость является вектором), стремится вращать тело вокруг положительного направления оси против часовой стрелки, и отрицательным, если она стремиться вращать тело по часовой стрелке. Условия Пространственной системы произвольно расположенных сил Произвольной пространственной системой сил называется система сил, линии действия которых не лежат в одной плоскости. Отсюда вытекает условие равновесия произвольной пространственной системы сил.
В геометрической форме: для равновесия произвольной пространственной системы сил необходимо и достаточно, чтобы главный вектор и главный момент системы равнялись нулю R = 0, Mo = 0. В аналитической форме: для равновесия произвольной пространственной системы сил необходимо и достаточно, чтобы суммы проекций всех сил на три координатные оси и суммы моментов всех сил относительно этих осей были равны нулю
ΣFkx = 0, ΣFky = 0, ΣFkz = 0, Mx(Fk) = 0, My(Fk) = 0, Mz(Fk) = 0. Центр тяжести. Способы определение центра тяжести. Координаты центра тяжести плоского тела и составленных сечений. Центр тяжести Центр тяжести тела - точка приложения силы тяжести (равнодействующей гравитационных сил).
Центр тяжести делит расстояние между двумя грузами в отношении, обратном отношению их масс. Определение центра тяжести Определение центра тяжести произвольного тела путем последовательного сложения сил, действующих на отдельные его части,— трудная задача; она облегчается только для тел сравнительно простой формы. Пусть тело состоит только из двух грузов с массами m1 и m2, соединенных стержнем (рис. 126). Если масса стержня мала по сравнению с массами m1 и m2, то ею можно пренебречь. На каждую из масс действует сила тяжести: P1=m1g, Р2=m2g; обе они направлены вертикально вниз, т. е. параллельно друг другу. Как мы уже знаем, равнодействующая двух параллельных сил приложена в точке О, которая определяется из условия
Следовательно, центр тяжести делит расстояние между двумя массами в отношении обратном отношению масс. Если это тело подвесить в точке О, оно останется в равновесии.
Скорость точки Скорость точки
Ускорение точки Ускорение точки
Поступательные движения твердого тела
Вращательное движение твердого. Частные Случаи вращательного движения твердого тела. ПОСТУПАТЕЛЬНОЕ И ВРАЩАТЕЛЬНОЕ ДВИЖЕНИЯ ТВЕРДОГО ТЕЛА 9.1. Поступательное движение Поступательное движени е - это такое движение твердого тела, при котором любая прямая соединяющая две точки тела, движется, оставаясь параллельной самой себе. Поступательное движение нельзя смешивать с прямолинейным, так как при поступательном движении траектория может быть какой угодно. Свойства поступательного движения характеризует следующая теорема: Все точки твердого тела, движущегося поступательно, описывают одинаковые траектории и в каждый момент времени имеют одинаковые по модулю и направлению скорости и ускорения. Пусть дано твердое тело совершающее поступательное движение относительно системы отсчета Oxyz (рис. 49 Выберем произвольные точки A и В характеризующиеся радиус-векторами Проведем вектор
Так как тело движется поступательно, то траекторию точки А получим из траектории точки В параллельным смещением всех точек на отрезок Продифференцируем уравнение (9.1.1):
Взяв производную от (9.1.3), получаем
т.е. скорости и ускорения всех точек твердого тела одинаковы. 9.2. Угловая скорость
Углова́я ско́рость — векторная величина, являющаяся 0%90%D0%BA%D1%81%D0%B8%D0%B0%D0%BB%D1%8C%D0%BD%D1%8B%D0%B9_%D0%B2%D0%B5%D0%BA%D1%82%D0%BE%D1%80"псевдовектором (аксиальным вектором) и характеризующая скорость 0%92%D1%80%D0%B0%D1%89%D0%B0%D1%82%D0%B5%D0%BB%D1%8C%D0%BD%D0%BE%D0%B5_%D0%B4%D0%B2%D0%B8%D0%B6%D0%B5%D0%BD%D0%B8%D0%B5"вращения 0%9C%D0%B0%D1%82%D0%B5%D1%80%D0%B8%D0%B0%D0%BB%D1%8C%D0%BD%D0%B0%D1%8F_%D1%82%D0%BE%D1%87%D0%BA%D0%B0"материальной точки вокруг центра вращения. Вектор угловой скорости по величине равен 0%A3%D0%B3%D0%BE%D0%BB"углу поворота точки вокруг центра вращения в единицу времени:
Углово́е ускоре́ние — 0%9F%D1%81%D0%B5%D0%B2%D0%B4%D0%BE%D0%B2%D0%B5%D0%BA%D1%82%D0%BE%D1%80"псевдовекторная 0%A4%D0%B8%D0%B7%D0%B8%D1%87%D0%B5%D1%81%D0%BA%D0%B0%D1%8F_%D0%B2%D0%B5%D0%BB%D0%B8%D1%87%D0%B8%D0%BD%D0%B0"физическая величина, характеризующая быстроту изменения 0%A3%D0%B3%D0%BB%D0%BE%D0%B2%D0%B0%D1%8F_%D1%81%D0%BA%D0%BE%D1%80%D0%BE%D1%81%D1%82%D1%8C"угловой скорости 0%9C%D0%B0%D1%82%D0%B5%D1%80%D0%B8%D0%B0%D0%BB%D1%8C%D0%BD%D0%B0%D1%8F_%D1%82%D0%BE%D1%87%D0%BA%D0%B0"материальной точки. При 0%92%D1%80%D0%B0%D1%89%D0%B5%D0%BD%D0%B8%D0%B5"вращении точки вокруг неподвижной 0%9E%D1%81%D1%8C_%D0%B2%D1%80%D0%B0%D1%89%D0%B5%D0%BD%D0%B8%D1%8F"оси, угловое ускорение по модулю равно0%A3%D0%B3%D0%BB%D0%BE%D0%B2%D0%BE%D0%B5_%D1%83%D1%81%D0%BA%D0%BE%D1%80%D0%B5%D0%BD%D0%B8%D0%B5"[1]:
Вектор углового ускорения При вращении вокруг неподвижной точки вектор углового ускорения определяется как первая производная от вектора угловой скорости
и направлен по касательной к 0%93%D0%BE%D0%B4%D0%BE%D0%B3%D1%80%D0%B0%D1%84"годографу вектора Существует связь между 0%A2%D0%B0%D0%BD%D0%B3%D0%B5%D0%BD%D1%86%D0%B8%D0%B0%D0%BB%D1%8C%D0%BD%D0%BE%D0%B5_%D1%83%D1%81%D0%BA%D0%BE%D1%80%D0%B5%D0%BD%D0%B8%D0%B5"тангенциальным и угловым ускорениями:
где R — 0%A0%D0%B0%D0%B4%D0%B8%D1%83%D1%81_%D0%BA%D1%80%D0%B8%D0%B2%D0%B8%D0%B7%D0%BD%D1%8B"радиус кривизны 0%A2%D1%80%D0%B0%D0%B5%D0%BA%D1%82%D0%BE%D1%80%D0%B8%D1%8F_%D0%BC%D0%B0%D1%82%D0%B5%D1%80%D0%B8%D0%B0%D0%BB%D1%8C%D0%BD%D0%BE%D0%B9_%D1%82%D0%BE%D1%87%D0%BA%D0%B8"траектории точки в данный момент времени. Итак, угловое ускорение равно второй производной от угла поворота по времени или первой производной от угловой скорости по времени. Угловое ускорение измеряется в рад/с². Мгновенный центр скоростей
Аксиомы динамики Первая аксиома динамики. Существуют системы отсчета, в которых материальная точка покоится, либо движется прямолинейно и равномерно, если она не подвергается воздействиям. Такие системы отсчета называют инерциальными. Инерциальные системы отсчета эквивалентны в том смысле, что в них одинаково соблюдаются все законы механики. Воздействие на материальную точку со стороны какого-либо объекта характеризуется силой. Вторая аксиома динамики. Если в инерциальной системе отсчета материальная точка движется с ускорением (рис. 1), то на нее действует сила, пропорциональная ускорению. Коэффициентом пропорциональности является масса точки. Третья аксиома динамики. Силовое воздействие всегда сопровождается таким же по величине силовым противодействием. Из третьей аксиомы следует, что материальная точка всегда противодействует ускоряющему ее объекту. Согласно второй аксиоме, сила такого противодействия. Методы кинематики Кинема́тика (0%93%D1%80%D0%B5%D1%87%D0%B5%D1%81%D0%BA%D0%B8%D0%B9_%D1%8F%D0%B7%D1%8B%D0%BA"греч. κινειν — двигаться) в физике — раздел 0%9C%D0%B5%D1%85%D0%B0%D0%BD%D0%B8%D0%BA%D0%B0"механики, изучающий математическое описание (средствами 0%93%D0%B5%D0%BE%D0%BC%D0%B5%D1%82%D1%80%D0%B8%D1%8F"геометрии, 0%90%D0%BB%D0%B3%D0%B5%D0%B1%D1%80%D0%B0"алгебры, 0%9C%D0%B0%D1%82%D0%B5%D0%BC%D0%B0%D1%82%D0%B8%D1%87%D0%B5%D1%81%D0%BA%D0%B8%D0%B9_%D0%B0%D0%BD%D0%B0%D0%BB%D0%B8%D0%B7"математического анализа…) движения идеализированных тел (0%9C%D0%B0%D1%82%D0%B5%D1%80%D0%B8%D0%B0%D0%BB%D1%8C%D0%BD%D0%B0%D1%8F_%D1%82%D0%BE%D1%87%D0%BA%D0%B0"материальная точка, 0%90%D0%B1%D1%81%D0%BE%D0%BB%D1%8E%D1%82%D0%BD%D0%BE_%D1%82%D0%B2%D0%B5%D1%80%D0%B4%D0%BE%D0%B5_%D1%82%D0%B5%D0%BB%D0%BE"абсолютно твердое тело, 0%98%D0%B4%D0%B5%D0%B0%D0%BB%D1%8C%D0%BD%D0%B0%D1%8F_%D0%B6%D0%B8%D0%B4%D0%BA%D0%BE%D1%81%D1%82%D1%8C"идеальная HYPERLINK "http://ru.wikipedia.org/wiki/%D0%98%D0%B4%D0%B5%D0%B0%D0%BB%D1%8C%D0%BD%D0%B0%D1%8F_%D0%B6%D0%B8%D0%B4%D0%BA%D0%BE%D1%81%D1%82%D1%8C"жидкость), без рассмотрения причин движения (0%9C%D0%B0%D1%81%D1%81%D0%B0"массы, 0%A1%D0%B8%D0%BB%D0%B0"сил и т. д.). Исходные понятия кинематики — 0%9F%D1%80%D0%BE%D1%81%D1%82%D1%80%D0%B0%D0%BD%D1%81%D1%82%D0%B2%D0%BE_%D0%B2_%D1%84%D0%B8%D0%B7%D0%B8%D0%BA%D0%B5"пространство и 0%92%D1%80%D0%B5%D0%BC%D1%8F"время. Например, если тело движется по окружности, то кинематика предсказывает необходимость существования 0%A6%D0%B5%D0%BD%D1%82%D1%80%D0%BE%D1%81%D1%82%D1%80%D0%B5%D0%BC%D0%B8%D1%82%D0%B5%D0%BB%D1%8C%D0%BD%D0%BE%D0%B5_%D1%83%D1%81%D0%BA%D0%BE%D1%80%D0%B5%D0%BD%D0%B8%D0%B5"центростремительного ускорения без уточнения того, какую природу имеет сила, его порождающая. Причинами возникновения 0%9C%D0%B5%D1%85%D0%B0%D0%BD%D0%B8%D1%87%D0%B5%D1%81%D0%BA%D0%BE%D0%B5_%D0%B4%D0%B2%D0%B8%D0%B6%D0%B5%D0%BD%D0%B8%D0%B5"механического движения занимается другой раздел механики — 0%94%D0%B8%D0%BD%D0%B0%D0%BC%D0%B8%D0%BA%D0%B0_(%D1%84%D0%B8%D0%B7%D0%B8%D0%BA%D0%B0)"динамика.
Общие теоремы динамик Методи сечения Метод сечений позволяет определить внутренние силы, которые возникают встержне, находящемся в равновесии под действием внешней нагрузки. Рассмотрим идеально упругий призматический стержень прямоугольного поперечного сечения (рис. 1.2, а). Выделим внутри стержня какие-либо две частицы K и L, расположенные на бесконечно малом расстоянии друг от друга. Для большей наглядности предположим, что между этими частицами имеется некоторая пружинка, удерживающая их на определенном расстоянии друг от друга. Пусть натяжение пружинки равно нулю.
Метод сечений состоит из четырех последовательных этапов: разрезать, отбросить, заменить, уравновесить. Разрежем стержень, находящийся в равновесии под действием некоторой системы сил Отбросим одну из частей стержня и рассмотрим оставленную часть. Поскольку мы как бы разрезали бесчисленное множество пружинок, соединявших бесконечно близкие частицы тела, разделенного теперь на две части, в каждой точке поперечного сечения стержня необходимо приложить силы упругости, которые при деформации тела возникли между этими частицами. Иными словами, заменим действие отброшенной части внутренними силами (рис. 1.3, б).
Растяжение и сжатие Растяжением или сжатием называют вид нагружения, при котором в поперечном сечении бруса возникает только один внутренний силовой фактор -продольная сила.
Рассмотрим брус, нагруженный внешними силами вдоль оси. Брус закреплён в стене (закрепление «заделка») (рис. 30.) Участком закрепления считают часть бруса между внешними силами.
Продольная сила положительна, участок 1 растянут. Участок 2:
=F. Продольная сила положительна, участок 2 растянут.
Эпюрой продольной силы называется график распределения продольной силы вдоль от бруса. Продольное сжатие Разрушение при продольном сжатии может происходить в различных формах, которые показаны на рис.1: - микровыпучивание волокон при упругом или пластическом состоянии матрицы; - микровыпучивание волокон после нарушения адгезионной связи между ними и матрицей; - расслаивание; - выпучивание слоя; - сдвиговое разрушение слоя; - разделение слоев из-за поперечного растяжения в направлении толщины слоя (поперечное расслаивание от растяжения). Микровыпучивание волокон при упругих напряжениях в матрице возникает в слоях с весьма малой объемной долей волокон. Переход матрицы в пластическое состояние и отслаивание волокон от матрицы возникает, как правило, при объемной доле волокон y? 0,4. Экспериментальные данные по продольному сжатию показывают, что слой не может выдерживать достаточно высокую сжимающую нагрузку, чтобы достигнуть полной прочности. При разрушении слоя от сжимающей нагрузки напряжение в волокнах значительно меньше их ожидаемой прочности на сжатие.
а – микровыпучивание; б – отслаивание волокна от матрицы; в – выпучивание слоя; г – сдвиговые разрушения Расчет на срез и смятие
Напряжение при кручении Вращающийся стержень, работающий на кручение называют 0%92%D0%B0%D0%BB_(%D1%82%D0%B5%D1%85%D0%BD%D0%B8%D0%BA%D0%B0)"валом. Стержень, используемый как упругий элемент, который работает на скручивание, называется 0%A2%D0%BE%D1%80%D1%81%D0%B8%D0%BE%D0%BD"торсионом. Касательные напряжения
где r — расстояние от оси кручения. Очевидно, что касательные напряжения достигают наибольшего значения на поверхности вала при
где Wp — 0%9F%D0%BE%D0%BB%D1%8F%D1%80%D0%BD%D1%8B%D0%B9_%D0%BC%D0%BE%D0%BC%D0%B5%D0%BD%D1%82_%D1%81%D0%BE%D0%BF%D1%80%D0%BE%D1%82%D0%B8%D0%B2%D0%BB%D0%B5%D0%BD%D0%B8%D1%8F&action=edit&redlink=1"полярный момент сопротивления. Это даёт возможность записать условие прочности при кручении в таком виде:
Используя это условие, можно или по известным силовым факторам, которые создают крутящий момент Т, найти полярный момент сопротивления и далее, в зависимости от той или иной формы, найти размеры сечения, или наоборот — зная размеры сечения, можно вычислить наибольшую величину крутящего момента, которую можно допустить в сечении, которое в свою очередь, позволит найти допустимые величины внешних нагрузок. Изгиб. Основные понятия Изгиб — вид деформации, при котором происходит искривление осей прямых 0%91%D1%80%D1%83%D1%81_(%D0%BC%D0%B5%D1%85%D0%B0%D0%BD%D0%B8%D0%BA%D0%B0)"брусьев или изменение 0%9A%D1%80%D0%B8%D0%B2%D0%B8%D0%B7%D0%BD%D0%B0"кривизны осей кривых брусьев. Изгиб связан с возникновением в поперечных сечениях бруса изгибающих моментов. Прямой изгиб возникает в случае, когда 0%98%D0%B7%D0%B3%D0%B8%D0%B1%D0%B0%D1%8E%D1%89%D0%B8%D0%B9_%D0%BC%D0%BE%D0%BC%D0%B5%D0%BD%D1%82"изгибающий момент в данном поперечном сечении бруса действует в плоскости, проходящей через одну из главных центральных осей инерции этого сечения. В случае, когда плоскость действия изгибающего момента в данном поперечном сечении бруса не проходит ни через одну из главных осей инерции этого сечения, называется косым. Если при прямом или косом изгибе в поперечном сечении бруса действует только изгибающий момент, то соответственно имеется чистый прямой или чистый косой изгиб. Если в поперечном сечении действует также и поперечная сила, то имеется поперечный прямой или поперечный косой изгиб. Часто термин «прямой» в названии прямого чистого и прямого поперечного изгиба не употребляют и их называют соответственно чистым изгибом и поперечным изгибом. Лекция 6. Плоский изгиб Изгибом называется вид нагружения бруса, при котором к нему прикладывается момент, лежащий в плоскости проходящей через продольную ось. В поперечных сечениях бруса возникают изгибающие моменты. При изгибе возникают деформация, при которой происходит искривление оси прямого бруса или изменение кривизны кривого бруса. Брус, работающий при изгибе, называется балкой. Конструкция, состоящая из нескольких изгибаемых стержней, соединенных между собой чаще всего под углом 90°, =07K205BAO рамой. Изгиб называется плоским или прямым, если плоскость действия нагрузки проходит через главную центральную ось инерции сечения (рис.6.1).
Рис.6.1
При плоском поперечном изгибе в балке возникают два вида внутренних усилий: поперечная сила Q и изгибающий момент M. В раме при плоском поперечном изгибе возникают три усилия: продольная N, поперечная Q силы и изгибающий момент M. Если изгибающий момент Косой изгиб - изгиб, при котором нагрузки действуют в одной плоскости, не совпадающей с главными плоскостями инерции. Сложный изгиб - изгиб, при котором нагрузки действуют в различных (произвольных) плоскостях. Далее будем рассматривать плоский изгиб, то есть все силы будем прилагать в плоскости симметрии балки.
Рис.6.2
Осваивать расчет балок и рам удобно, рассматривая по очереди следующие вопросы: - Определение внутренних усилий в балках и построение эпюр внутренних усилий. - Проверка прочности балок. - Определение перемещений и проверка жесткости балок. Решение этих вопросов получим в соответствующих разделах на примере конкретных задач. ГИПОТЕЗА ПРОЧНОСТИ МОРА Согласно гипотезе прочности Мора, предложенной Отто Мором, два напряженных состояния равноопасны, если для соответствующих главных напряжений Условие прочности по гипотезе прочности Мора: Гипотеза прочности Мора не учитывает влияния второго главного напряжения ( Коэффициент Гипотеза прочности Мора рекомендуется для хрупких материалов. Для пластичных материалов гипотеза прочности Мора тождественна третьей гипотезе прочности.
Критическая сила
Проинтегрировав это выражение и учитывая при этом граничные условия, Л. Эйлером получено уравнение для определения критической силы:
где
При изменении условий закрепления стержня величина критической силы изменяется. На схеме (рис. 2.24, г) изображен стержень длиной
где (
Рис. 2.25. Способы закрепления стержня
Рис.2. Цилиндрическая фрикционная Рис.3. Коническая фрикционная передача 2. По взаимному расположению осей валов: - цилиндрические или конусные с параллельными осями (рис.1, 2); - конические с пересекающимися осями (рис.3). 3. В зависимости от условий работы: - открытые (работают всухую); - закрытые (работают в масляной ванне). В открытых фрикционных передачах коэффициент трения 4. По принципу действия: - нереверсивные (рис.1-3, 11 и 12); - реверсивные (рис.10). 5. Различают также передачи с постоянным или автоматическим регулируемым прижатием катков, с промежуточным (паразитным) фрикционным элементом или без него.
Достоинства фрикционных передач: - простота конструкции и обслуживания; - плавность передачи движения и регулирования скорости и бесшумность работы; - большие кинематические возможности (преобразование вращательного движения в поступательное, бесступенчатое изменение скорости, возможность реверсирования на ходу, включение и выключение передачи на ходу без остановки); - за счет возможностей пробуксовки передача обладает предохранительными свойствами. Однако после пробуксовки передача, как правило, резко ухудшает свои качества - появляются лыски на катках, неравномерно срабатываются фрикционные поверхности и т.д. Поэтому использовать пробуксовку как предохранительное средство не рекомендуется; - отсутствие мёртвого хода при реверсе передачи; - равномерность вращения, что удобно для приборов; - возможность бесступенчатого регулирования передаточного числа, причем на ходу, без остановки передачи.
Недостатки: - непостоянство передаточного числа из-за проскальзывания; - незначительная передаваемая мощность (открытые передачи - до 10-20 кВт; закрытые - до 200-300 кВт); - для открытых передач сравнительно низкий КПД; - большое и неравномерное изнашивание катков при буксовании; - необходимость применения опор валов специальной конструкции с прижимными устройствами (это делает передачу громоздкой); - для силовых открытых передач незначительная окружная скорость ( - Большие нагрузки на валы и подшипники от прижимной силы - большие потери на трение.
Применение. Фрикционные передачи с нерегулируемым передаточным числом в машиностроении применяются сравнительно редко, например, во фрикционных прессах, молотах, лебедках, буровой технике и т.п.). В качестве силовых передач они громоздки и малонадежны. Эти
|
||||||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 1243; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.012 с.) |




 тогда
тогда
 средняя скорость точки за промежуток времени Dt. Скорость точки в данный момент времени
средняя скорость точки за промежуток времени Dt. Скорость точки в данный момент времени
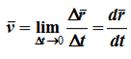
 Скорость точки – это кинематическая мера ее движения, равная производной по времени от радиус-вектора этой точки в рассматриваемой системе отсчета. Вектор скорости направлен по касательной к траектории точки в сторону движения.
Скорость точки – это кинематическая мера ее движения, равная производной по времени от радиус-вектора этой точки в рассматриваемой системе отсчета. Вектор скорости направлен по касательной к траектории точки в сторону движения.
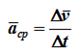 характеризует изменение вектора скорости за малый промежуток времени Δt. Ускорение точки в данный момент времени
характеризует изменение вектора скорости за малый промежуток времени Δt. Ускорение точки в данный момент времени

 Ускорение точки – это мера изменения ее скорости, равная производной по времени от скорости этой точки или второй производной от радиус-вектора точки по времени. Ускорение характеризует изменение вектора скорости по величине и направлению и направлено в сторону вогнутости траектории.
Ускорение точки – это мера изменения ее скорости, равная производной по времени от скорости этой точки или второй производной от радиус-вектора точки по времени. Ускорение характеризует изменение вектора скорости по величине и направлению и направлено в сторону вогнутости траектории.
 ).
). в момент времени t.
в момент времени t.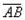 , тогда
, тогда
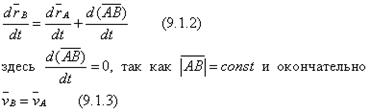
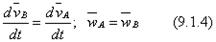
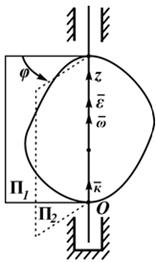 Быстрота изменения угла φ – это угловая скорость:
ω=dφ/dt=φ', рад/с; с-1. (2.3)
Приняв k как единичный орт положительного направления оси, получим
Быстрота изменения угла φ – это угловая скорость:
ω=dφ/dt=φ', рад/с; с-1. (2.3)
Приняв k как единичный орт положительного направления оси, получим
 Вектор угловой скорости – скользящий вектор: он может быть приложен к любой точке оси вращения и всегда направлен вдоль оси, при положительном значении угловой скорости направления ω и k совпадают, при отрицательном – противоположны.
Изменение угловой скорости характеризуется угловым ускорением:
Вектор угловой скорости – скользящий вектор: он может быть приложен к любой точке оси вращения и всегда направлен вдоль оси, при положительном значении угловой скорости направления ω и k совпадают, при отрицательном – противоположны.
Изменение угловой скорости характеризуется угловым ускорением:
 Вектор углового ускорения так же направлен по оси вращения. При ускоренном вращении их направления совпадают, при замедленном - противоположны.
Для некоторых частных случаев вращательного движения могут быть использованы формулы:
- равномерное вращение (ω - const)
φ=φ0+ωt; (2.5)
- равнопеременное вращение (ε - const)
ω=ω0+εt; φ=φ0+ω0t+εt2/2. (2.6)
В технике угловая скорость часто задается в оборотах в минуту n[об/мин]. Один оборот – это 2π радиан:
ω=n⋅2π/60=nπ/30 рад/с; с-1.
Вектор углового ускорения так же направлен по оси вращения. При ускоренном вращении их направления совпадают, при замедленном - противоположны.
Для некоторых частных случаев вращательного движения могут быть использованы формулы:
- равномерное вращение (ω - const)
φ=φ0+ωt; (2.5)
- равнопеременное вращение (ε - const)
ω=ω0+εt; φ=φ0+ω0t+εt2/2. (2.6)
В технике угловая скорость часто задается в оборотах в минуту n[об/мин]. Один оборот – это 2π радиан:
ω=n⋅2π/60=nπ/30 рад/с; с-1.
 ,
,
 направлен вдоль оси вращения (в сторону
направлен вдоль оси вращения (в сторону  при ускоренном вращении и противоположно
при ускоренном вращении и противоположно  по времени0%A3%D0%B3%D0%BB%D0%BE%D0%B2%D0%BE%D0%B5_%D1%83%D1%81%D0%BA%D0%BE%D1%80%D0%B5%D0%BD%D0%B8%D0%B5"[2], то есть
по времени0%A3%D0%B3%D0%BB%D0%BE%D0%B2%D0%BE%D0%B5_%D1%83%D1%81%D0%BA%D0%BE%D1%80%D0%B5%D0%BD%D0%B8%D0%B5"[2], то есть ,
, ,
,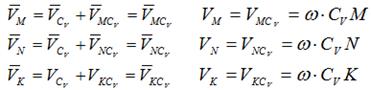 Из рис. 1.5 видно, что мгновенный центр скоростей лежит в точке пересечения перпендикуляров, проведенных к скоростям точек, при этом всегда справедливо соотношение
Из рис. 1.5 видно, что мгновенный центр скоростей лежит в точке пересечения перпендикуляров, проведенных к скоростям точек, при этом всегда справедливо соотношение

 Рис. 1.5
На нижеприведенных рисунках показаны примеры определения положения мгновенного центра скоростей и приведены формулы для расчета скоростей точек.
Рис. 1.5
На нижеприведенных рисунках показаны примеры определения положения мгновенного центра скоростей и приведены формулы для расчета скоростей точек.
 Для рисунка 1.6:
1. СV совпадает с точкой В VB=0. Шатун АВ вращается вокруг точки В
Для рисунка 1.6:
1. СV совпадает с точкой В VB=0. Шатун АВ вращается вокруг точки В
 2.
2.
 3. МЦС лежит в «бесконечности»
3. МЦС лежит в «бесконечности»

 22. Теорема сложение скоростей
22. Теорема сложение скоростей

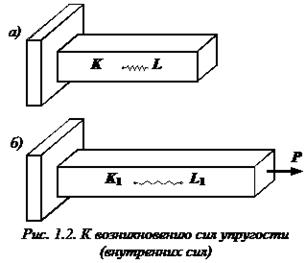 Приложим теперь к стержню растягивающую силу
Приложим теперь к стержню растягивающую силу  (рис. 1.2, б). Пусть в результате деформации стержня, частица K перейдет в положение
(рис. 1.2, б). Пусть в результате деформации стержня, частица K перейдет в положение  , а частица L – в положение
, а частица L – в положение  . Соединяющая эти частицы пружинка при этом растянется. После снятия внешней нагрузки частицы вернутся в первоначальное положение K и L благодаря усилию, которое возникло в пружинке. Сила, которая возникла между частицами (в пружинке) в результате деформации идеально упругого стержня, называются силой упругости или внутренней силой. Она может быть найдена методом сечений.
. Соединяющая эти частицы пружинка при этом растянется. После снятия внешней нагрузки частицы вернутся в первоначальное положение K и L благодаря усилию, которое возникло в пружинке. Сила, которая возникла между частицами (в пружинке) в результате деформации идеально упругого стержня, называются силой упругости или внутренней силой. Она может быть найдена методом сечений. (рис. 1.3, а) на две части плоскостью, перпендикулярной к его оси z.
(рис. 1.3, а) на две части плоскостью, перпендикулярной к его оси z.

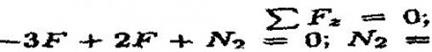




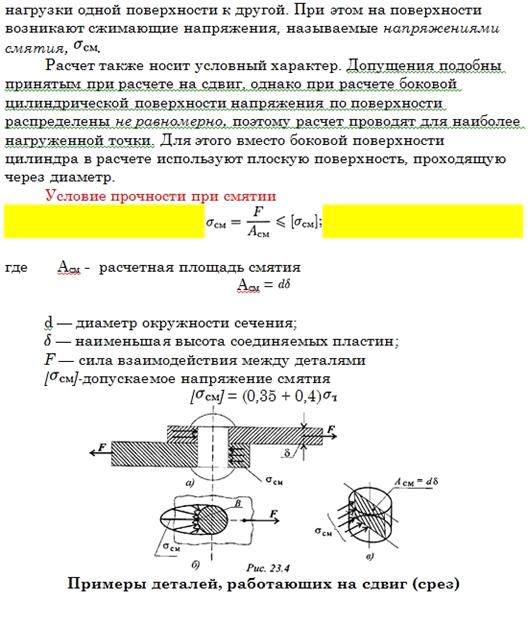
 , возникающие в условиях кручения, определяются по формуле:
, возникающие в условиях кручения, определяются по формуле: ,
, и при максимальном крутящем моменте
и при максимальном крутящем моменте  , то есть
, то есть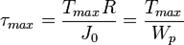 ,
, .
.
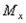 является единственным внутренним силовым фактором, то такой изгиб называется чистым (рис.6.2). При наличии поперечной силы
является единственным внутренним силовым фактором, то такой изгиб называется чистым (рис.6.2). При наличии поперечной силы  изгиб называется поперечным. Строго говоря, к простым видам сопротивления относится лишь чистый изгиб; поперечный изгиб относят к простым видам сопротивления условно, так как в большинстве случаев (для достаточно длинных балок) действием поперечной силы при расчетах на прочность можно пренебречь.
изгиб называется поперечным. Строго говоря, к простым видам сопротивления относится лишь чистый изгиб; поперечный изгиб относят к простым видам сопротивления условно, так как в большинстве случаев (для достаточно длинных балок) действием поперечной силы при расчетах на прочность можно пренебречь.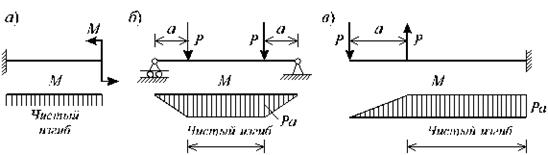
 и
и 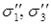 соблюдается соотношение:
соблюдается соотношение:  .
.
 ).
). представляет собой отношение предельных напряжений, соответствующих одноосным растяжению и сжатию, который равен для хрупких материалов:
представляет собой отношение предельных напряжений, соответствующих одноосным растяжению и сжатию, который равен для хрупких материалов: 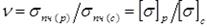 , для пластичных:
, для пластичных:  .
. .Пусть при достижении силы критического значения
.Пусть при достижении силы критического значения  стержень сохраняет изогнутую форму и находится в равновесии (рис.2.24, б). В сечении, отстоящем на расстоянии
стержень сохраняет изогнутую форму и находится в равновесии (рис.2.24, б). В сечении, отстоящем на расстоянии 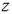 от начала координат, действует изгибающий момент
от начала координат, действует изгибающий момент  .
Если предположить, что потеря устойчивости происходит при напряжениях, не превышающих предела пропорциональности
.
Если предположить, что потеря устойчивости происходит при напряжениях, не превышающих предела пропорциональности  , и что имеют место лишь малые отклонения от прямолинейной формы, то дифференциальное уравнение изогнутой оси стержня принимает вид (см. п. 2.5.5):
, и что имеют место лишь малые отклонения от прямолинейной формы, то дифференциальное уравнение изогнутой оси стержня принимает вид (см. п. 2.5.5):
 .
При потере устойчивости стержень изгибается в плоскости наименьшей жесткости, т.е. поперечные
сечения стержня будут поворачиваться вокруг той оси, относительно которой момент инерции имеет минимальное значение. Поэтому следует считать
.
При потере устойчивости стержень изгибается в плоскости наименьшей жесткости, т.е. поперечные
сечения стержня будут поворачиваться вокруг той оси, относительно которой момент инерции имеет минимальное значение. Поэтому следует считать  .
Поскольку прогиб
.
Поскольку прогиб  и вторая производная от него
и вторая производная от него  всегда имеют разные знаки, то
всегда имеют разные знаки, то  и
и 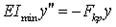 .
.
 Рис. 2.24. Устойчивость сжатых стержней
Рис. 2.24. Устойчивость сжатых стержней
 ,
,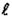 – длина стержня;
– длина стержня;  – любое целое число (n =1; 2; 3 и т.д.). При n =1 (рис. 2.24, в) стержень изгибается по одной полуволне синусоиды (устойчивое равновесие), а при всех последующих значениях n число полуволн равно номеру соответствующей критической силы (равновесие неустойчивое). Для практических расчетов интерес представляет наименьшая критическая сила:
– любое целое число (n =1; 2; 3 и т.д.). При n =1 (рис. 2.24, в) стержень изгибается по одной полуволне синусоиды (устойчивое равновесие), а при всех последующих значениях n число полуволн равно номеру соответствующей критической силы (равновесие неустойчивое). Для практических расчетов интерес представляет наименьшая критическая сила: . (2.71)
. (2.71) вместо
вместо  , (2.72)
, (2.72) ) – приведенная длина стержня;
) – приведенная длина стержня; 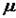 – коэффициент приведения, показывающий, во сколько раз следует изменить длину шарнирно-закрепленного стержня, чтобы значение критической силы для него было бы равно критической силе
– коэффициент приведения, показывающий, во сколько раз следует изменить длину шарнирно-закрепленного стержня, чтобы значение критической силы для него было бы равно критической силе 
 выше, прижимное усилие катков Fn меньше. В закрытых фрикционных передачах масляная ванна обеспечивает хороший отвод тепла, делает скольжение менее опасным, увеличивает долговечность передачи.
выше, прижимное усилие катков Fn меньше. В закрытых фрикционных передачах масляная ванна обеспечивает хороший отвод тепла, делает скольжение менее опасным, увеличивает долговечность передачи. 7 - 10 м/с);
7 - 10 м/с); , что увеличивает их размеры и делает передачу громоздкой. Этот недостаток ограничивает величину передаваемой мощности;
, что увеличивает их размеры и делает передачу громоздкой. Этот недостаток ограничивает величину передаваемой мощности;


