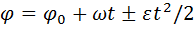Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Момент силы относительно точки и осиСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
Основные понятия статики Теоретическая механика — наука, изучающая общие законы механического движения и механического взаимодействия материальных тел. Мех. движением называется перемещение тела по отношению к другому телу, происходящее в пространстве и времени. Мех. взаимодействием называется такое взаимодействие материальных тел, которое изменяет или стремится изменить характер их мех. движения. Статика — раздел механики, в котором изучаются методы преобразования систем сил в эквивалентные системы и устанавливаются условия равновесия сил, приложенных к твердому телу. Материальное тело, размеры которого в рассматриваемых конкретных условиях можно не учитывать, называют материальной точкой (МТ). МТ обладает массой и способностью взаимодействовать с другими телами. Системой МТ или механической системой называется такая совокупность МТ, в которой положение и движение каждой точки зависят от положения и движения других точек этой системы. Тела, расстояния между любыми точками которых остаются неизменными, называют абсолютно твердыми. Кинематическое состояние тела — состояние покоя или движения определенного характера. Сила — мера механического взаимодействия тел, определяющая интенсивность и направление этого взаимодействия. Сила определяется тремя элементами: числовым значением (модулем), направлением и точкой приложения. Изображается сила вектором. Прямая, по которой направлена сила называется, называется линией действия силы. Совокупность нескольких сил, действующих на данное тело, называется системой сил. Системы сил, под действием каждой из которых твердое тело находится в одинаковом кинематическом состоянии, называются эквивалентными. Сила, эквивалентная некоторой системе сил, называется равнодействующей. Сила, равная по модулю равнодействующей и направленная по линии ее действия в противоположную сторону, называется уравновешивающей силой. Система сил, которая, будучи приложенной к твердому телу, находящемуся в состоянии покоя, не выводящая его из этого состояния, называется системой взаимно уравновешивающихся сил. Внешними называются силы, действующие на МТ (тела) данной системы со стороны МТ (тел), не принадлежащих этой системе. Внутренними называются силы взаимодействия между МТ (телами) рассматриваемой системы. Аксиомы статики 1) Аксиома инерции. Под действием взаимно уравновешивающихся сил материальная точка (тело) находится в состоянии покоя или движется равномерно прямолинейно. 2) Аксиома равновесия двух сил. Две силы, приложенные к твердому телу, взаимно уравновешиваются только в том случае, если их модули равны, и они направлены по одной линии прямой в противоположные стороны. 3) Аксиома присоединения и исключения уравновешивающихся сил. Действие системы сил на твердое тело не изменится, если к ней присоединить или из нее исключить систему взаимно уравновешивающихся сил. Следствие. Не изменяя кинематического состояния абсолютно твердого тела, силу можно переносить вдоль линии ее действия, сохраняя неизменными ее модуль и направление. 4) Аксиома параллелограмма сил. Равнодействующая двух пересекающихся сил приложена в точке их пересечения и изображается диагональю параллелограмма, построенного на этих силах.
φ – угол между направлениями сил 5) Аксиома равенства действия и противодействия. Всякому действию соответствует равное по величине и противоположное по направлению противодействие. 6) Аксиома сохранения равновесия сил, приложенных к деформирующемуся телу при его затвердении. Равновесие сил приложенных к деформирующемуся телу сохраняется при его затвердении.
Связи и их реакции Тело называется свободным, если оно может перемещаться в пространстве в любом направлении. Тело, ограничивающие свободу движения данного твердого тела, является по отношению к нему связью. Твердое тело, свобода движения которого ограничена связями, называется несвободным. Задаваемые силы выражают действие на твердое тело других тел, вызывающих или свободных вызвать изменение его кинематического состояния. Реакцией связи называется сила или система сил, выражающая механическое действие связи на тело. Принцип освобождаемости твердых тел от связей — несвободное твердое тело можно рассматривать как свободное, на которое кроме задаваемых сил действуют реакции связей.
Теорема Пуансо Приведение силы к заданному центру (метод Пуансо) – силу можно перенести параллельно самой себе в любую точку плоскости, если добавить соответствующую пару сил, момент которой равен моменту этой силы относительно рассматриваемой точки. Добавим к системе в точке A две силы, равные по величине между собой и величине заданной силы, направленные по одной прямой в противоположные стороны параллельно заданной силе.
Кинематическое состояние не изменилось (аксиома о присоединении). Исходная сила и одна из добавленных сил противоположно направленная образуют пару сил. Момент этой пары численно равен моменту исходной силы относительно центра приведения. Во многих случаях пару сил удобно изображать дуговой стрелкой.
Центр параллельных сил При сложении двух параллельных сил две параллельные приводятся к одной силе — равнодействующей, линия действия которой направлена параллельно линиям действия сил. Равнодействующая приложена в точке делящей прямую, на расстояния обратно пропорциональные величинам сил.
Поскольку силу можно переносить по линии ее действия, то точка приложения равнодействующей не определена. Если силы повернуть на один и тот же угол и вновь произвести сложение сил, то получим другое направление линии действия равнодействующей. Точка пересечения этих двух линий равнодействующих может рассматриваться как точка приложения равнодействующей, не изменяющая своего положения при повороте всех сил одновременно на один и тот же угол. Такая точка называется центром параллельных сил.
Теорема Вариньона Теорема о моменте равнодействующей силы: момент равнодействующей относительно любой точки равен геометрической сумме моментов составляющих сил относительно этой точки, а момент равнодействующей силы относительно оси равен алгебраической сумме моментов составляющих сил относительно этой оси. Определим момент равнодействующей силы
Тогда Проекция момента равнодействующей на произвольную ось
Фермы. Методы расчета ферм
Способ вырезания узлов. Суть способа заключается в том, что мысленно вырезают каждый узел фермы, прикладывают к нему известные силы и реакции стержней, которые направляют от узла, т.к. неизвестно какие стержни фермы растянуты, а какие сжаты, изначально полагают, что все стержни растянуты, а затем составляются уравнения равновесия сил, приложенных к каждому узлу. Расчет фермы начинают с узлов, к которым приложено не более двух неизвестных сил для плоской фермы, и не более трех для пространственной. Метод Риттера. Ферму разделяют на две части сечением, проходящим через три стержня, в которых (или в одном из которых) требуется определить усилия, и рассматривают равновесие одной из этих частей. Действие отброшенной части заменяют соответствующими силами, направляя их вдоль разрезанных стержней от узлов, т. е. считая их растянутыми. Затем составляют уравнения моментов относительно точек Риттера (точка пересечения двух из трех перерезанных стержней). Из полученных уравнений определяются усилия в стержнях.
Сила трения. Законы трения Силы трения скольжения появляются при скольжении одного тела по поверхности другого в плоскости соприкосновения тел. Часто приходится учитывать действие этих сил при изучении равновесия тел. С этой целью используются приближенные законы трения, полученные опытным путем: 1. Сила трения возникает лишь тогда, когда приложенные к телу силы стремятся сдвинуть его или оно уже скользит по поверхности другого тела. Сила трения направлена в сторону, противоположную направлению движения или в сторону, противоположную той, в которую приложенные силы стремятся сдвинуть тело. 2. В конкретных условиях сила трения может принимать любые значения в пределах от нуля до некоторого придельного значения 3. Величина предельной силы трения пропорциональна силе нормального давления N между трущимися поверхностями и не зависит от величины площади соприкасания тел:
где Наибольший угол, на который может отклониться линия действия силы реакции негладкой поверхности от нормали, проведенной к ней в точке контакта тел, называется углом трения скольжения. Тангенс угла скольжения равен коэффициенту трения скольжения:
Под действием силы Значение
Основные понятия кинематики. Скорость точки. Ускорение Кинематикой называют раздел механики, в котором движение тел рассматривается без выяснения причин, его вызывающих. Механическим движением тела называют изменение его положения в пространстве относительно других тел с течением времени. Тело, относительно которого рассматривается положение изучаемого тела, называется телом отсчета. Перемещаясь с течением времени из одной точки в другую, тело (материальная точка) описывает некоторую линию, которую называют траекторией движения тела. Перемещением тела называют направленный отрезок прямой, соединяющий начальное положение тела с его последующим положением. Перемещение есть векторная величина. Пройденный путь l равен длине дуги траектории, пройденной телом за некоторое время t. Путь – скалярная величина. Скорость — векторная величина, характеризующая быстроту и направление движения точки в данной системе отсчета. Для характеристики движения вводится понятие средней скорости:
Мгновенная скорость определяется как предел, к которому стремится средняя скорость на бесконечно малом промежутке времени Δt:
Ускорение — быстрота изменения модуля и направления скорости точки. Среднее ускорение:
Мгновенное ускорение:
Поступательное движение тела. Задание движения. Распределение скоростей и ускорений точек тела Поступательным движением твердого тела называется такое движение, при котором любая прямая, соединяющая две точки тела, движется параллельно самой себе. Теорема. Все точки твердого тела, движущегося поступательно, описывают одинаковые (совпадающие при наложении) траектории и в каждый момент времени имеют геометрически равные скорости и ускорения. Уравнениями поступательного движения твердого тела являются уравнения движения любой точки этого тела — обычно уравнения движения его центра тяжести:
Общие для всех точек твердого тела, движущегося поступательно, скорость
Вращательное движение. Задание движения Вращательным называется такое движение тела, при котором остаются неподвижными все его точки, лежащие на некоторой прямой, называемой осью вращения. При этом движении все остальные точки тела движутся в плоскостях перпендикулярных оси вращения, и описывают окружности, центры которых лежат на этой оси. При вращении тела угол поворота Величина, характеризующая быстроту изменения угла поворота
Величина, характеризующая быстроту изменения угловой скорости с течением времени, называется угловым ускорением тела.
Уравнение равномерного вращения тела. Вращение тела с постоянной скоростью называется равномерным.
Уравнение равнопеременного вращения тела. Вращение тела, при котором угловое ускорение постоянно, называют равнопеременным вращением.
Основные понятия статики Теоретическая механика — наука, изучающая общие законы механического движения и механического взаимодействия материальных тел. Мех. движением называется перемещение тела по отношению к другому телу, происходящее в пространстве и времени. Мех. взаимодействием называется такое взаимодействие материальных тел, которое изменяет или стремится изменить характер их мех. движения. Статика — раздел механики, в котором изучаются методы преобразования систем сил в эквивалентные системы и устанавливаются условия равновесия сил, приложенных к твердому телу. Материальное тело, размеры которого в рассматриваемых конкретных условиях можно не учитывать, называют материальной точкой (МТ). МТ обладает массой и способностью взаимодействовать с другими телами. Системой МТ или механической системой называется такая совокупность МТ, в которой положение и движение каждой точки зависят от положения и движения других точек этой системы. Тела, расстояния между любыми точками которых остаются неизменными, называют абсолютно твердыми. Кинематическое состояние тела — состояние покоя или движения определенного характера. Сила — мера механического взаимодействия тел, определяющая интенсивность и направление этого взаимодействия. Сила определяется тремя элементами: числовым значением (модулем), направлением и точкой приложения. Изображается сила вектором. Прямая, по которой направлена сила называется, называется линией действия силы. Совокупность нескольких сил, действующих на данное тело, называется системой сил. Системы сил, под действием каждой из которых твердое тело находится в одинаковом кинематическом состоянии, называются эквивалентными. Сила, эквивалентная некоторой системе сил, называется равнодействующей. Сила, равная по модулю равнодействующей и направленная по линии ее действия в противоположную сторону, называется уравновешивающей силой. Система сил, которая, будучи приложенной к твердому телу, находящемуся в состоянии покоя, не выводящая его из этого состояния, называется системой взаимно уравновешивающихся сил. Внешними называются силы, действующие на МТ (тела) данной системы со стороны МТ (тел), не принадлежащих этой системе. Внутренними называются силы взаимодействия между МТ (телами) рассматриваемой системы. Аксиомы статики 1) Аксиома инерции. Под действием взаимно уравновешивающихся сил материальная точка (тело) находится в состоянии покоя или движется равномерно прямолинейно. 2) Аксиома равновесия двух сил. Две силы, приложенные к твердому телу, взаимно уравновешиваются только в том случае, если их модули равны, и они направлены по одной линии прямой в противоположные стороны. 3) Аксиома присоединения и исключения уравновешивающихся сил. Действие системы сил на твердое тело не изменится, если к ней присоединить или из нее исключить систему взаимно уравновешивающихся сил. Следствие. Не изменяя кинематического состояния абсолютно твердого тела, силу можно переносить вдоль линии ее действия, сохраняя неизменными ее модуль и направление. 4) Аксиома параллелограмма сил. Равнодействующая двух пересекающихся сил приложена в точке их пересечения и изображается диагональю параллелограмма, построенного на этих силах.
φ – угол между направлениями сил 5) Аксиома равенства действия и противодействия. Всякому действию соответствует равное по величине и противоположное по направлению противодействие. 6) Аксиома сохранения равновесия сил, приложенных к деформирующемуся телу при его затвердении. Равновесие сил приложенных к деформирующемуся телу сохраняется при его затвердении.
Связи и их реакции Тело называется свободным, если оно может перемещаться в пространстве в любом направлении. Тело, ограничивающие свободу движения данного твердого тела, является по отношению к нему связью. Твердое тело, свобода движения которого ограничена связями, называется несвободным. Задаваемые силы выражают действие на твердое тело других тел, вызывающих или свободных вызвать изменение его кинематического состояния. Реакцией связи называется сила или система сил, выражающая механическое действие связи на тело. Принцип освобождаемости твердых тел от связей — несвободное твердое тело можно рассматривать как свободное, на которое кроме задаваемых сил действуют реакции связей.
Момент силы относительно точки и оси Момент силы — векторная величина, равная произведению радиус-вектора, проведенного от оси вращения к точке приложения силы на вектор этой силы. МС характеризует вращательное действие этой силы на твердое тело.
Алгебраическим моментом силы относительно точки (центра момента) называется взятое со знаком «+» или «-» произведение величины силы на плече силы.
Плечо силы — кратчайшее расстояние от точки центра момента до линии действия силы. Правило знаков: если сила стремится повернуть тело вокруг точки центра момента против часовой стрелки ставится знак «+», если по часовой знак «-». Из определения следует, что момент силы относительно точки равен нулю лишь в том случае, когда плече силы равно нулю, т.е. линия действия силы проходит через точку центр момента. Момент силы относительно оси — момент проекции силы на плоскость перпендикулярную оси взятый относительно точки пересечения оси и плоскости.
Правило знаков: если с острия оси видеть вращение плоскости под действием проекции силы против часовой стрелки ставится знак «+», если по часовой — знак «-». Из определения следует что момент силы относительно оси равен нулю если: 1) сила пересекает ось (h=0) 2) сила параллельна оси (Fp=0) 3) сила совпадает с осью (h=0 и Fp=0) Для вычисления момента силы относительно оси необходимо: 1) Выбрать плоскость перпендикулярную оси; 2) Спроецировать силу на эту плоскость; 3) Найти точку пересечения оси и плоскости; 4) Определить плечо относительно точки; 5) Определить знак момента.
|
||||||||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 2475; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.252.58 (0.008 с.) |



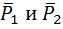




 , приложенной в точке К, относительно произвольно выбранного центра приведения О:
, приложенной в точке К, относительно произвольно выбранного центра приведения О:
 , что сформулировано в первой части теоремы.
, что сформулировано в первой части теоремы. проходящую через точку O равна:
проходящую через точку O равна:
 – угол между осью
– угол между осью  и направлением
и направлением  .
.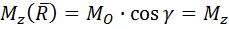
 , что сформулировано во второй части теоремы.
, что сформулировано во второй части теоремы. Фермой называется геометрически не изменяемая шарнирно-стрежневая конструкция. Если все оси фермы лежат в одной плоскости, то ферму называют плоской. Точки, в которых сходятся оси стержней, называют узлами фермы, а те узлы, которыми ферма опирается на основание, называются опорными узлами. Стержни плоской фермы, расположенные по верхнему контуру, образуют верхний пояс фермы, а расположенные по нижнему контуру — нижний пояс фермы. Вертикальные стержни называются стойками, а наклонные — раскосами.
Фермой называется геометрически не изменяемая шарнирно-стрежневая конструкция. Если все оси фермы лежат в одной плоскости, то ферму называют плоской. Точки, в которых сходятся оси стержней, называют узлами фермы, а те узлы, которыми ферма опирается на основание, называются опорными узлами. Стержни плоской фермы, расположенные по верхнему контуру, образуют верхний пояс фермы, а расположенные по нижнему контуру — нижний пояс фермы. Вертикальные стержни называются стойками, а наклонные — раскосами. , которое достигается в состоянии относительного проскальзывания или в состоянии предельного равновесия тела.
, которое достигается в состоянии относительного проскальзывания или в состоянии предельного равновесия тела. ,
, – коэффициент трения скольжения.
– коэффициент трения скольжения.
 Трением качения называется сопротивление, возникающие при качении одного тела по поверхности другого. Трение качения возникает оттого, что поверхность катящегося тела и плоскость, по которой тело катится, не абсолютно тверды, а несколько деформируются вследствие давления тела на плоскость.
Трением качения называется сопротивление, возникающие при качении одного тела по поверхности другого. Трение качения возникает оттого, что поверхность катящегося тела и плоскость, по которой тело катится, не абсолютно тверды, а несколько деформируются вследствие давления тела на плоскость.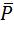 – вес колеса и его линия действия проходит через центр О катка. Приложим в этой точке горизонтальную силу
– вес колеса и его линия действия проходит через центр О катка. Приложим в этой точке горизонтальную силу  . В месте контакта катка и поверхности возникает сила трения скольжения
. В месте контакта катка и поверхности возникает сила трения скольжения  , препятствующая проскальзыванию катка.
, препятствующая проскальзыванию катка. смещается в сторону действия силы
смещается в сторону действия силы 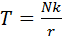 .
. 


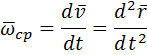

 ускорение
ускорение  называют скоростью и ускорением поступательного движения твердого тела.
называют скоростью и ускорением поступательного движения твердого тела. изменяется в зависимости от времени:
изменяется в зависимости от времени:  .
. с течением времени называется угловой скоростью тела.
с течением времени называется угловой скоростью тела.