
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Свободные колебания материальной точкиСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
ДИНАМИКА МАТЕРИАЛЬНОЙ ТОЧКИ 1. Основные понятия и определения Основное уравнение динамики:
где Дифференциальные уравнения движения материальной точки в координатной форме:
Две основные задачи динамики точки: Первая (прямая) задача: Зная массу точки и законы ее движения, найти действующую на точку силу. Для решения этой задачи дважды дифференцируем законы движения по времени (определяем
Тогда модуль силы:
направляющие косинусы:
Вторая (обратная) задача: По заданной массе точки и действующей на точку силе определить движение этой точки. Для решения этой задачи необходимо в левую часть уравнений подставить массу m, а в правую часть проекции действующей силы. Полученные дифференциальные уравнения дважды проинтегрировать по времени с учетом начальных условий.
Примеры решения задач 2.1 Частица массой m, несущая заряд электричества e, находится в однородном электрическом поле с переменным напряжением Решение 1. Расчетная схема.
2. На точку М действует сила 3. Составим дифференциальное уравнение движения точки М в проекции на ось у:
4. Разделим переменные и проинтегрируем:
Перепишем уравнение, разделим переменные и проинтегрируем ещё раз:
2.2 Тело весом Р, находящееся на гладкой горизонтальной плоскости, притягивается к центру О на этой плоскости силой, обратно пропорциональной квадрату расстояния тела от точки О. В начальный момент тело находилось от притягивающего центра на расстоянии b и имело скорость, равную нулю. Сила притяжения тела в этот момент была равна
Решение 1. Расчетная схема
Силы 1. Составим дифференциальное уравнение движения точки М в проекции на ось х: 2. В дифференциальном уравнении три переменных:
2.3 Корабль массой 107 кг движется со скоростью 16 м/с. Сопротивление воды пропорционально квадрату скорости корабля и равно 3.105 Н при скорости 1 м/с. Какое расстояние пройдет корабль, прежде чем его скорость станет равной 4 м/с? За какое время корабль пройдет это расстояние? Решение Так как корабль (твердое тело) совершает поступательное движение и размеры корабля не существенны для условий данной задачи, то заменим корабль материальной точкой. 1. Изобразим материальную точку М в выбранной системе координат в текущий момент времени. Покажем также начальное М0 и конечное М1положения материальной точки. Назовем это расчетной схемой. Расчетная схема:
3. Составляем дифференциальное уравнение движения точки М в проекции на ось х:
Так как движение прямолинейное, то
4. Решим дифференциальное уравнение (1), для чего разделим переменные и проинтегрируем:
При t = t 1, V = V 1: t 1 = 6,25 c. Далее нужно найти S 1 и здесь есть два варианта: а) уравнение (2) представить в виде
разделить переменные и проинтегрировать в пределах от 0 до t 1 (t 1 известно), найти S 1; б) чаще используется такой вариант для случая, когда R=R (V): запишем дифференциальное уравнение (1), умножим обе части на dx: 100 .V.dV = – 3 .V2dx, разделим переменные и проинтегрируем
Вариант второй предпочтительнее, так как быстрее приводит к ответу.
2.4 Подводная лодка, не имевшая хода, получив небольшую отрицательную плавучесть P, погружается на глубину, двигаясь поступательно. Сопротивление воды при небольшой отрицательной плавучести можно принять пропорциональным первой степени скорости погружения и равным kSV, где k — коэффициент пропорциональности; S — площадь горизонтальной проекции лодки; V — величина скорости погружения. Масса лодки равна М. Определить скорость погружения V, если при t = 0 скорость V 0 = 0.
Решение
1. Расчетная схема
где μ = k.S) 3. Составим дифференциальное уравнение движения точки М в проекции на ось х:
4. Решим уравнение (1). Разделим переменные и проинтегрируем (используя метод замены переменной):
Пропотенцируем:
Можно рекомендовать и другой путь решения дифференциального уравнения (1):
где Окончательно получаем
Это обыкновенное линейное неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентами. Как известно, решение таких уравнений ищется в виде х = х 1 +х 2, где х 1 — общее решение однородного дифференциального уравнения. Для нахождения общего решения решаем характеристическое уравнение
Его корни: Теперь можно найти Найдем х 2 — частное решение уравнения (1):
Подставляя Итак, Получим два уравнения: 0 = С 1 +С 2;
Теперь с учетом С 1 и С 2
Мы определили закон движения подводной лодки. Найдем
Результаты совпали.
2.5 Материальная точка массой m отталкивается от центра силой, пропорциональной расстоянию (коэффициент пропорциональности mk 2). Сопротивление среды пропорционально скорости движения (коэффициент пропорциональности 2 mk 1). В начальный момент точка находилась на расстоянии b от центра, и её скорость в этот момент равнялась нулю. Найти закон движения точки.
Решение 1.Расчетная схема
3. Составим дифференциальное уравнение движения точки М в проекции на ось x:
Для нахождения с 1 и с 2, определим Решим полученные уравнения совместно:
Примеры решения задач на прямолинейные колебания
1. Составляем расчётную схему. Объект исследования — платформа весом P совершает прямолинейные колебания вдоль вертикальной оси, следовательно её можно представить как материальную точку. Изобразим на расчётной схеме вертикальную ось x, направленную вниз, покажем на ней положение недеформированной пружины О1 (рис. 2,а). Начало координат О выбираем в положении статического равновесия (рис. 2,б) нашего объекта исследования. Условия статичекого равновесия записываются в виде:
(1)
В начальный момент времени пружина была сдеформирована под статическим действием платформы и груза, на рис. 2,в покажем начальное положение точки — М0, эта точка также соответствует статическому равновесию платформы с грузом. Введём обозначения: fст — статическая деформация пружины; fст2 — статическая деформация пружины под действием платформы и груза; x 0 — начальная координата точки; x — координата точки в произвольном положении. Произвольное положение объекта исследования покажем на рис. 2,г. Отметим характерные точки О1, О, М, М0 на расчётной схеме (рис. 2,д). Начальные условия колебаний запишутся в виде
2. На материальную точку действуют силы:
3. Составляем дифференциальное уравнение движения точки в форме второго закона Ньютона.
или в проекции на ось x:
Для определения статической деформации в дифференциальное уравнение (3) подставим условия статического равновесия (1):
Подставив fст в дифференциальное уравнение и проведя несложные преобразования, получим
где 4. Решаем дифференциальное уравнение. Дифференциальное уравнение (5) описывает случай свободных незатухающих колебаний и его решение ищется в виде
Для определения постоянных интегрирования C 1 и C 2 подставим в (6) начальные условия (2), для чего предварительно найдём первую производную от уравнения движения:
Откуда выразим
1. Составляем расчётную схему. Объект исследования — груз весом P, исследуемое движение — прямолинейные колебания вдоль вертикальной оси. Следовательно груз можно представить как материальную точку. Изобразим на расчётной схеме вертикальную ось x, направленную вниз, покажем на ней положение недеформированной балки О1 (рис. 2,а). Начало координат О выбираем в положении статического равновесия (рис. 2,б) нашего объекта исследования. Условия статичекого равновесия записываются в виде:
В начальный момент времени балка находилась в недеформированном положении. Скорость груза в этот момент определяется из условий его равноускоренного движения под действием силы тяжести.
На рис. 2.в покажем начальное положение точки — М0. Введём обозначения: fст — статическая деформация балки; x 0 — начальная координата точки; x — координата точки в произвольном положении. Произвольное положение объекта исследования покажем на рис. 2,г. Отметим характерные точки О1,О, М, М0 на расчётной схеме (рис. 2,д). Начальные условия колебаний запишутся в виде
2. На материальную точку действуют силы:
3. Составляем дифференциальное уравнение движения точки в форме второго закона Ньютона.
или в проекции на ось x:
Для определения статической деформации в дифференциальное уравнение (3) подставим условия статического равновесия (1):
Подставив fст в дифференциальное уравнение и проведя несложные преобразования, получим
где 4. Решаем дифференциальное уравнение. Дифференциальное уравнение (5) описывает случай свободных незатухающих колебаний и его решение ищется в виде
Для определения постоянных интегрирования C 1 и C 2 подставим в (6) начальные условия (2), для чего предварительно найдём первую производную от уравнения движения:
Откуда выразим
Силы инерции. Метод кинетостатики Методом кинетостатики называется искусственный прием, позволяющий записать уравнения движения в виде уравнений статики, основанный на принципе Даламбера. Если система состоит из нескольких тел, то к каждому телу, помимо активных сил и сил реакций связей, прикладываются соответствующие силы инерции, после чего составляются уравнения равновесия. При решении задач методом кинетостатики рекомендуется следующая последовательность действий: 1) Выбрать систему, «движение» которой рассматривается, определить вид движения каждого из тел системы; 2) Выбрать систему координат; 3) Составить уравнения равновесия для каждого из тел системы, предварительно расчленив систему по внутренним связям на отдельные тела, где это необходимо; 4) Решить уравнения равновесия и исследовать ответ. Расчленять систему целесообразно, если она состоит из нескольких тел, и когда вычисление сил инерции вызывает затруднения.
Пример решения задачи
Однородный барабан массы М3 и радиуса R присоединен шарнирно двумя ненагруженными стержнями АС и ВС к стене. На барабан намотана невесомая нерастяжимая нить, к одному концу которой присоединены два груза, массами М1 и М2 соответственно, соединенные нитью, а на другой конец действует постоянная сила Р. Найти усилия в стержных АС и ВС.
Рассмотрим систему тел 1, 2 и 3. Тела 1 и 2 совершают поступательное движение, тело 3 вращается вокруг оси Выберем систему координат Активными силами будут: Приложим соответствующие силы инерции
Составим уравнения равновесия
Решая эту систему, получим
Для отыскания значений сил инерции
Из кинематики известно, что
откуда, после дифференцирования, получаем
Подставим (1.9) в (1.7), получим
Из (1.10) находим
Находим соответствующие силы инерции
Подставляя значения
Оценивая полученные значения, можно предположить, что стержень ВС растянут, а стержень АС – сжат.
Пример решения задачи.
Плоский механизм с идеальными связями находится в равновесии под действием сил
Для решения задачи воспользуемся ПВП, согласно которому
где Рассматриваемый механизм имеет одну степень свободы. Его элементы (звенья) совершают следующие виды движений: кривошип ОА и О1В – вращательное движение относительно осей, проходящих через точки О и О1, треугольник АВС и шатун D – поступательное. Чтобы составить уравнение (2.3), сообщим механизму возможное перемещение и введем следующие обозначения для перемещений звеньев, к которым приложены активные силы: Примем за независимое возможное перемещение Сначала найдем возможное перемещение общей для звеньев ОА и АВС точки А. При вращательном движении звена ОА относительно точки О имеем
Направление Для определения возможного перемещения точки С находим мгновенный центр вращения звена АВС, зная линии действия перемещений двух точек А и В этого звена - Тогда линейные возможные перемещения точек А, В и С будут пропорциональны их расстояниям до мгновенного центра вращения:
Находим угловое перемещение звена АВС:
его направление определяется направлением Далее находим и изображаем линейное перемещение точки С
где
В случае необходимости находим по направлению Зная Запишем
Направление Теперь запишем уравнение (1) для механизма:
Так как
откуда
После подстановки исходных данных находим
Механической системы
При движении материальной системы, подчиненной идеальным удерживающим связям, сумма работ активных сил и сил инерции на любых возможных перемещениях точек системы равна нулю:
то общее уравнение динамики имеет вид:
Преимущество общего уравнения динамики по сравнению с другими теоремами динамики заключается в том, что в его формулировке отсутствуют реакции идеальных связей. Если не все связи являются идеальными, например, имеются связи с трением, то, применяя общее уравнение динамики, следует к активным силам добавлять реакции, соответствующие неидеальным связям. Вычисление суммы работ сил инерции на возможных перемещениях точек твердого тела производится по формулам:
а) При поступательном движении:
где
б) При вращении вокруг неподвижной оси:
где
в) При плоском движении:
где
При решении задач с помощью общего уравнения динамики рекомендуется следующая последовательность действий: 1) Изобразить на рисунке активные и реакции, соответствующие неидеальным связям (силы трения); 2) Определить главные векторы и главные моменты сил инерции масс системы; 3) Дать возможное перемещение одной из точек системы и выразить возможные перемещения точек приложения всех сил, указанных в 1, 2, через это возможное перемещение. 4) Вычислить сумму работ всех сил на возможных перемещениях точек системы; составить общее уравнение динамики, приравняв в вычисленную сумму работ сил нулю; 5) Определить искомую величину либо провести интегрирование дифференциального уравнения движения.
Пример решения задачи.
Рис.2.1.
Механическая система состоит из ступенчатого шкива 2 (радиусы ступеней R2 и r2), груза 1 и сплошного катка 3, прикрепленных к концам нитей, намотанных на ступени шкива. На шкив при его вращении действует момент сил сопротивления M2 Радиус инерции ступенчатого шкива 2 Дано: R2 = R, r2 = 0,6 R, Р1 = 6Р, Р3 = 3Р, М2 = 0,2 РR, F = 2P, Pz2 = 0,5R, f = 0,1, α = 30˚, β = 60˚, γ = 60˚. Определить: а1 – ускорение груза 1.
1. Материальная система состоит из трех твердых тел и имеет одну степень свободы. Будем считать, что ускорение груза 1
2. Определим
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 972; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.41 (0.011 с.) |

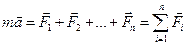 , (1)
, (1) - равнодействующая системы сил.
- равнодействующая системы сил. ;
;  ;
; 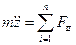 .
. ,
,  ,
, 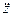 ); подставляем в дифференциальное уравнение; находим проекции силы
); подставляем в дифференциальное уравнение; находим проекции силы  :
: ,
,  ,
,  .
. ;
; ;
;  ;
;  .
. (A и k — заданные постоянные). Определить движение частицы, если известно, что в электрическом поле на частицу действует сила
(A и k — заданные постоянные). Определить движение частицы, если известно, что в электрическом поле на частицу действует сила 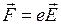 , направленная в сторону напряжения
, направленная в сторону напряжения  . Влиянием силы тяжести пренебречь. Начальное положение частицы принять за начало координат; начальная скорость частицы равна нулю.
. Влиянием силы тяжести пренебречь. Начальное положение частицы принять за начало координат; начальная скорость частицы равна нулю. Из условий задачи понятно, что точка М (тело) будет двигаться вдоль оси у (точка M0 совпадает с О; V 0=0).
Из условий задачи понятно, что точка М (тело) будет двигаться вдоль оси у (точка M0 совпадает с О; V 0=0).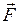 (
(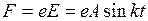 ).
).
 ;
; 
 ;
; 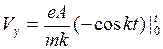 ;
;  .
. ;
; , откуда
, откуда .
. . Определить скорость тела, после того как оно пройдёт половину первоначального расстояния до точки О.
. Определить скорость тела, после того как оно пройдёт половину первоначального расстояния до точки О.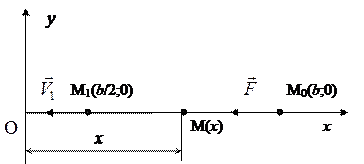 2. На точку М действуют силы:
2. На точку М действуют силы:  (P=mg);
(P=mg);  (N — нормальная реакция плоскости, N=P);
(N — нормальная реакция плоскости, N=P);  где K1 — коэффициент пропорциональности. По условию в точке М0 выполнялось равенство
где K1 — коэффициент пропорциональности. По условию в точке М0 выполнялось равенство  , отсюда найдём K 1= kP, т.е.
, отсюда найдём K 1= kP, т.е.  )
) и
и 
 Умножим обе части уравнения на
Умножим обе части уравнения на  и зная, что
и зная, что  , получим
, получим  , проинтегрируем:
, проинтегрируем: отсюда
отсюда 
 2. На точку М действуют силы:
2. На точку М действуют силы:  —сила тяжести,
—сила тяжести,  (выталкивающая сила Архимеда), сила сопротивления
(выталкивающая сила Архимеда), сила сопротивления  Н, где μ — коэффициент сопротивления ([ μ ] =
Н, где μ — коэффициент сопротивления ([ μ ] =  ). Из условий задачи следует, что
). Из условий задачи следует, что 

 . (1)
. (1)
 (2)
(2) :
:  , откуда
, откуда . (3)
. (3) ,
,

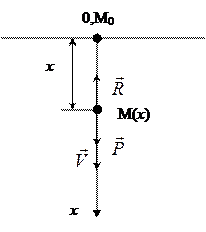 2. Силы, действующие на точку М:
2. Силы, действующие на точку М:
 . (1)
. (1) ;
; ;
; ;
;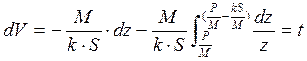 ;
; ;
;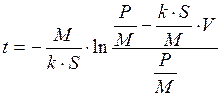 ;
; ;
; .
.
 ,
, ;
;  .
. .
.
 .
. .
.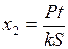 .
. и
и  в дифференциальное уравнение (1), видим, что х 2 является решением, так как обращает его в тождество.
в дифференциальное уравнение (1), видим, что х 2 является решением, так как обращает его в тождество. . Определим С 1и С 2 из начальных условий: t = 0, x 0 = 0, V 0 = 0. Вычислим
. Определим С 1и С 2 из начальных условий: t = 0, x 0 = 0, V 0 = 0. Вычислим  .
. ;
;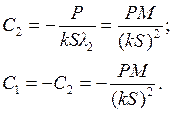
 .
. ;
; или
или 
 2. На точку М действуют силы:
2. На точку М действуют силы: ;
; .
. .
. его корни действительные
его корни действительные  . Решение дифференциального уравнения
. Решение дифференциального уравнения  .
. и запишем начальные условия:
и запишем начальные условия:  ;
; 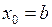 ;
;  ;
;  ;
;  .
.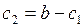 ;
;  ;
;  ;
;  ;
;  , таким образом,
, таким образом, 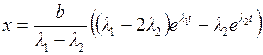 , где
, где  .
. 4.1 На платформе весом P, подрессоренной пружиной жесткостью c, покоится груз весом G. В некоторый момент времени груз толчком сбрасывается с платформы. Определите уравнение последующих колебаний платформы.
4.1 На платформе весом P, подрессоренной пружиной жесткостью c, покоится груз весом G. В некоторый момент времени груз толчком сбрасывается с платформы. Определите уравнение последующих колебаний платформы.

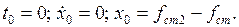 (2)
(2) — сила тяжести;
— сила тяжести; — сила упругости пружины (определяется как произведение жёсткости пружины на её полную деформацию, полную деформацию пружины определяем на расчётной схеме — это расстояние между концом недеформированной пружины (рис. 2,а) и произвольным положением точки (рис. 2,г)).
— сила упругости пружины (определяется как произведение жёсткости пружины на её полную деформацию, полную деформацию пружины определяем на расчётной схеме — это расстояние между концом недеформированной пружины (рис. 2,а) и произвольным положением точки (рис. 2,г)).
 . (3)
. (3) , откуда
, откуда . (4)
. (4) , (5)
, (5) — круговая частота свободных колебаний.
— круговая частота свободных колебаний. . (6)
. (6) ;
;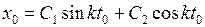 ;
; .
. (7)
(7)

 4.2 Груз весом P падает без начальной скорости с высоты h на упругую невесомую балку жесткостью c. Найдите уравнение колебаний груза, считая ось x проведенной вертикально вверх из положения статического груза на балке.
4.2 Груз весом P падает без начальной скорости с высоты h на упругую невесомую балку жесткостью c. Найдите уравнение колебаний груза, считая ось x проведенной вертикально вверх из положения статического груза на балке.

 — время падения;
— время падения; — скорость в момент касания с балкой.
— скорость в момент касания с балкой. (2)
(2)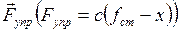 — сила упругости балки (определяется как произведение жёсткости балки на её полную деформацию, полную деформацию балки определяем на расчётной схеме — это расстояние между недеформированным положением балки (рис. 2,а) и произвольным положением точки (рис. 2,г)).
— сила упругости балки (определяется как произведение жёсткости балки на её полную деформацию, полную деформацию балки определяем на расчётной схеме — это расстояние между недеформированным положением балки (рис. 2,а) и произвольным положением точки (рис. 2,г)). . (3)
. (3) , откуда
, откуда
 , проходящей через точку С.
, проходящей через точку С.
 . Реакции связей
. Реакции связей  и
и  направлены вдоль стержней, которые считаем растянутыми.
направлены вдоль стержней, которые считаем растянутыми.
 и
и  . При этом считаем, что тело 3 вращается в сторону, определяемую направлением силы
. При этом считаем, что тело 3 вращается в сторону, определяемую направлением силы  .
.


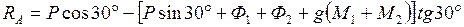
 и
и  , составим уравнение моментов относительно точки
, составим уравнение моментов относительно точки  и приравняем его нулю.
и приравняем его нулю.
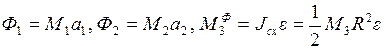 .
.
 ,
,







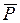 ,
, 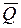 и пары сил с моментом
и пары сил с моментом  , приложенной к звену ОА. Используя принцип возможных перемещений, определить величину момента при следующих исходных данных:
, приложенной к звену ОА. Используя принцип возможных перемещений, определить величину момента при следующих исходных данных: 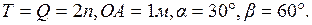 Звено АВС – прямоугольный треугольник с углом при вращении А, равным
Звено АВС – прямоугольный треугольник с углом при вращении А, равным 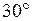 .
.
 - элементарные работы активных сил на соответствующих возможных перемещениях.
- элементарные работы активных сил на соответствующих возможных перемещениях. - угловое перемещение звена ОА,
- угловое перемещение звена ОА, 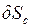 и
и  - линейные перемещения точек C и D.
- линейные перемещения точек C и D.
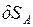 определяются направлением
определяются направлением  . Проводя перпендикуляры к направлениям
. Проводя перпендикуляры к направлениям  . При плоско-параллельном движении все точки звена АВС совершают вращательное движение относительно этой точки.
. При плоско-параллельном движении все точки звена АВС совершают вращательное движение относительно этой точки.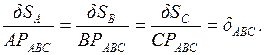

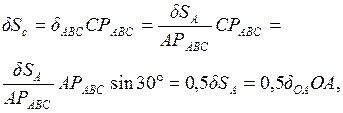
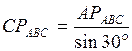 .
.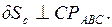 Направление
Направление  определяется направлением
определяется направлением 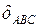 (вращение вокруг точки
(вращение вокруг точки 
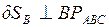 .
.


 за скобки, получим:
за скобки, получим:
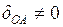 :
: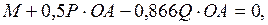
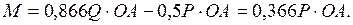


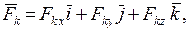
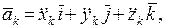



 - равнодействующая сил инерции (
- равнодействующая сил инерции ( );
);  - ускорение любой точки твердого тела;
- ускорение любой точки твердого тела; 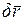 - возможное перемещение любой точки твердого тела.
- возможное перемещение любой точки твердого тела.
 - главный момент сил инерции относительно оси вращения
- главный момент сил инерции относительно оси вращения 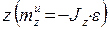 ;
;  - момент инерции твердого тела относительно оси вращения;
- момент инерции твердого тела относительно оси вращения;  - угловое ускорение вращательного движения твердого тела;
- угловое ускорение вращательного движения твердого тела;  - возможное угловое перемещение твердого тела.
- возможное угловое перемещение твердого тела.
 - главный вектор сил инерции
- главный вектор сил инерции  ;
;  - ускорение центра масс твердого тела;
- ускорение центра масс твердого тела; - главный момент сил инерции относительно оси, проходящей через центр масс С твердого тела перпендикулярно плоскости движения
- главный момент сил инерции относительно оси, проходящей через центр масс С твердого тела перпендикулярно плоскости движения  ;
;  - момент инерции твердого тела относительно оси, проходящей через центр масс С перпендикулярно плоскости движения;
- момент инерции твердого тела относительно оси, проходящей через центр масс С перпендикулярно плоскости движения;  - возможное перемещение центра масс С твердого тела;
- возможное перемещение центра масс С твердого тела;  - возможное угловое перемещение твердого тела.
- возможное угловое перемещение твердого тела.
 ρz2, f – коэффициент трения скольжения груза 1 о наклонную плоскость.
ρz2, f – коэффициент трения скольжения груза 1 о наклонную плоскость. направлено вниз по наклонной плоскости.
направлено вниз по наклонной плоскости.


