
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вынужденные колебания. Резонанс.Содержание книги
Поиск на нашем сайте Рассмотрим случай колебаний, когда на точку, кроме восстанавливающей силы F, действует ещё периодически изменяющаяся со временем сила
Эта сила называется возмущающей силой, колебания, происходящие при действии такой силы, называются вынужденными. Величина p – называется частотой возмущающей силы. Возмущающая сила может изменяться и по другому закону. Мы ограничимся, когда возмущающая сила изменяется по гармоническому закону. Вынужденные колебания при отсутствии сопротивления Дифференциальное уравнение движения имеет вид:
Разделим обе части на m и положим
Тогда учитывая обозначения (30), приведем уравнение движения к виду:
Уравнение (45) является дифференциальным уравнением вынужденных колебаний точки, при отсутствии сопротивления. Если решение состоит из общего и частного
Полагая, что
Где А – постоянная величина, которую надо подобрать так, чтобы уравнение (45) обратилось в тождество. Подставляя
Таким образом, частное решение будет:
Общее решение уравнения (45) имеет вид:
Где a и Решение (47) показывает, что колебания точки складывается из: 1. колебаний с амплитудой а (зависит от начальных условий) и частотой k, называемых собственными колебаниями; 2. колебаний с амплитудой А и частотой р, которые называются вынужденными колебаниями; благодаря наличию тех или иных сопротивлений, собственные колебания будут довольно быстро затухать. Поэтому основным значением в рассматриваемом движении имеют вынужденные колебания, закон которых даётся уравнением (46). Частота р вынужденных колебаний равна частоте возмущающее силы. Амплитуда этих колебаний, если разделить числитель и знаменатель
Где, согласно уравнения (30) и (44) от отклонения
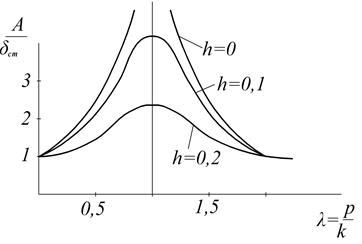
Рис. 3.13 h=0 при отсутствии сопротивления 1) При р=0 (или 2) При р=k амплитуда А становится очень большой 3) При В случае, когда р=k, т.е. частота возмущённой силы равна частоте собственных колебаний, имеет место так называемое явление резонанса. РАЗДЕЛ ЧЕТВЕРТЫЙ. ДИНАМИКА СИСТЕМЫ И ТВЕРДОГО ТЕЛА. Введение в динамику системы. Механическая система.
Механической системой материальных точек или тел называется такая их совокупность, в которой положение или движение каждой точки зависит от положения и движения всех остальных. Материальное тело будем рассматривать как систему материальных точек, образующих это тело. Примером может служить любая машина или механизм, в которой все тела связаны шарнирами, стержнями, тросами, ремнями и то подобном (то есть различными геометрическими связями). В этом случае на тела системы действуют силы взаимного давления или натяжения, передаваемые через связи. Совокупность тел, между которыми нет никаких сил взаимодействия (например, группа летящих самолетов), механическую систему не образуют. Внешними называют силы, действующие на точки системы со стороны точек или тел, не входящих в состав данной системы. Внутренними называют силы, действующие на точки системы со стороны других точек или тел этой же системы. Внутренние силы обладают следующими свойствами: 1. По третьему закону динамики любые две точки системы действуют друг на друга с равными по модулю и противоположно направлены. Так как аналогичный результат имеет место для любой пары точек системы, то Рис. 4.1 2. Сумма моментов (главный момент) всех внутренних сил системы относительно любого центра или оси равна нулю. Возьмем произвольный центр О. Из рисунка видно, что
Масса системы. Центр масс. Движение системы, кроме действующих сил, зависит от ее суммарной массы и распределения масс. Масса системы равна арифметической сумме масс всех точек или тел, образовавших систему.
В однородном поле тяжести, для которого
mк – массы материальных точек, хк, yк, zк – координаты этих точек. Геометрическая точка С, координаты которой определяются формулами (1), называется центром масс. Если положение центра масс определять его радиусом–вектором
где В однородном поле тяжести положения центра масс и центра тяжести совпадают. Понятие о центре тяжести, как о точке, через которую проходит линия действия равнодействующих сил тяжести – имеет только для твердого тела, находящегося в однородном поле тяжести. Понятие же о центре масс, как о характере распределения масс в системе материальных точек или тел, имеет смысл для любой системы материальных точек или тел.
|
||
|
Последнее изменение этой страницы: 2016-09-13; просмотров: 542; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.220 (0.006 с.) |

 , проекция
, проекция  равна
равна (43)
(43)
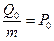 (44)
(44)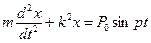 (45)
(45)
 частные решения
частные решения 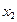 будем искать в виде:
будем искать в виде: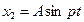 ,
, в уравнение(45) будем иметь
в уравнение(45) будем иметь

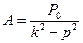
 (46)
(46) (47)
(47) постоянные интегрирования
постоянные интегрирования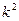 на, можно представить в виде:
на, можно представить в виде: (48)
(48) т.е.
т.е.  – величина статического отклонения точки под действием силы
– величина статического отклонения точки под действием силы  . Как видим, А зависит
. Как видим, А зависит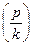 .
.
 ) амплитуда равна
) амплитуда равна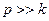 амплитуда А становится очень малой
амплитуда А становится очень малой Геометрическая сумма (главный вектор) всех внутренних сил системы равна нулю.
Геометрическая сумма (главный вектор) всех внутренних сил системы равна нулю. .
. . Аналогичный результат получится при вычислении моментов относительно оси
. Аналогичный результат получится при вычислении моментов относительно оси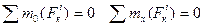 .
.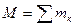 .
. , вес любой частицы тела будет пропорционален ее массе. Поэтому о распределении масс втеле можно судить по положению его центра тяжести.
, вес любой частицы тела будет пропорционален ее массе. Поэтому о распределении масс втеле можно судить по положению его центра тяжести.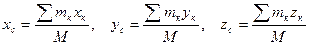 (1)
(1) , то из равенств (1)
, то из равенств (1) , (1/)
, (1/) – радиусы–векторы точек, образовавших систему.
– радиусы–векторы точек, образовавших систему.


