
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Раздел «Теоретическая механика»Содержание книги
Поиск на нашем сайте
В.В.ГАРАНИКОВ ТЕХНИЧЕСКАЯ МЕХАНИКА Раздел «Теоретическая механика» Тверь, 2011г. ПРЕДИСЛОВИЕ
Учебная дисциплина «Техническая механика» состоит из трех разделов: «Теоретическая механика», «Сопротивление материалов», «Детали машин». Согласно учебных планов для ряда специальностей раздел «Детали машин» изучается отдельно. Автором ставилась задача в сжатой и доступной форме изложить основные положения только одного раздела учебной дисциплины, а именно «Теоретической механики». Теоретическая механика – это наука, в которой изучаются общие законы механического движения твердых тел и механического взаимодействия материальных тел. Объем представленного материала соответствует программе дисциплины «Техническая механика», рекомендованной для данного направления подготовки бакалавров Министерством образования и науки Российской Федерации и учебному плану. Дисциплина «Техническая механика» является общепрофессиональной, обеспечивающей базовые знания при усвоении специальных дисциплин, изучаемых в дальнейшем. РАЗДЕЛ ПЕРВЫЙ СТАТИКА ТВЕРДОГО ТЕЛА ОСНОВНЫЕ ПОНЯТИЯ СТАТИКИ Введение
Теоретическая механика – это наука, в которой изучаются общие законы механического движения и механического взаимодействия материальных тел. Механического движением называется изменение с течением времени взаимного положения материальных точек в пространстве. Механическим взаимодействием называется такое взаимодействие материальных тел, которое изменяет характер их механического движения. Курс теоретической механики делится на три раздела: статику, кинематику и динамику. Статика – это раздел механики, в котором изучаются методы преобразования систем сил в эквивалентные системы и устанавливаются условия равновесия сил, приложенных к твердому телу. Кинематика – раздел механики, в котором изучается движение материальных тел в пространстве с геометрической точки зрения, вне связи с силами, определяющими это движение. Динамика – раздел механики, в котором изучается движение материальных тел в пространстве в зависимости от действующих на них сил. Материальное тело, размеры которого в рассматриваемых конкретных условиях можно не учитывать, называют материальной точкой. Материальная точка обладает массой и способностью взаимодействовать с другими телами. В теоретической механике рассматривают тела, расстояние между точками которых остаются неизменными. Такие тела называются абсолютно твердыми. Принимаем эту модель в качестве объекта исследования, пренебрегая возможными изменениями формы и размеров тела под действием нагрузок: считая, что 1) деформации малы – ими можно пренебречь 2) условие равновесия сил, приложенных к абсолютно твердому телу, являются необходимыми условиями равновесия любого тела. Важнейшими понятиями в теоретической механике является понятие силы. Сила – это мера механического взаимодействия тел, определяющая интенсивность и направление этого взаимодействия. Сила обозначается вектором.
Рис. 1.1 Сила определяется тремя элементами: числовым значением, направлением, точкой приложения. Силу измеряют в ньютонах. Совокупность нескольких сил, действующих на данное тело, называют системой сил
Если, не нарушая состояния тела, одну систему сил
В том случае, когда система сил Если абсолютно твердое тело останется в состоянии покоя при действии на него системы сил
Часто в этом случае говорят, что тело находится в равновесии. Силы, действующие на материальную систему, делятся на две группы: внешние и внутренние. Внешними называются силы, действующие на материальные точки данной системы со стороны материальных точек (тел), не принадлежащих этой системе. Внутренними называются силы взаимодействия между материальными точками рассматриваемой системы (силы межмолекулярного сцепления). Различаются: – сосредоточенные силы. Передаются через небольшую площадь или можно сказать в точке;
Рис. 1.2 – распределённые – передаются через определённую площадь
Рис.1.3 Аксиомы статики.
Данные аксиомы сформулированы на основе наблюдения и изучения окружающих нас явлений реального мира. Некоторые основные законы механики Галилея – Ньютона являются одновременно и аксиомами статики. 1. Аксиома инерции. Под действием взаимно уравновешивающихся сил материальная точка (тело) находится в состоянии покоя или движется прямолинейно и равномерно. Равномерное и прямолинейное движение материальной точки является движением по инерции. 2. Аксиома равновесия двух сил Две силы, приложенных к телу, взаимно уравновешиваются только в том случае, если их модули равны и если они направлены по одной прямой в противоположные стороны.
Рис. 1.4 3. Аксиома присоединения и исключения уравновешивающихся сил. Действие системы сил на твёрдое тело не изменяется, если к ней присоединить или из неё исключить систему взаимно уравновешивающихся сил.
Рис. 1.5 Пусть к твёрдому телу приложены силы Следствие. Не нарушая состояния абсолютно твёрдого тела, силу можно переносить вдоль линии её действия, сохраняя неизменными её модуль и направление.
Рис. 1.6 Предположим в т. А приложена Таким образом, силу можно переносить в любую точку по линии действия, не изменяя её модуля и направления. Поэтому в статике сила рассматривается как скользящий вектор. 4. Аксиома параллелограмма сил
Рис. 1.7 5. Аксиома равенства действия и противодействия Всякому действию соответствует равное и противоположно направленное противодействие. Эта аксиома утверждает, что силы действия друг на друга двух сил равны по модулю и направлены в противоположные стороны. Аксиома установлена Ньютоном.
Рис. 1.8 Рис. 1.9 В природе не существует одностороннего действия сил. Силы, действующие и противодействующие, приложены к разным телам, потому они не уравновешиваются. 6. Аксиома сохранения равновесия сил, приложенных к деформирующемуся телу при его затвердевании Равновесие сил, приложенных к деформирующемуся телу, сохраняется при его затвердении. Из этой, аксиомы следует, что условие равновесия сил приложенных к абсолютно твёрдому телу, должны и сохраняться для сил, приложенных к деформирующемуся телу. Однако в случае деформированного тела эти условия необходимы, но не достаточны.
Рис. 1.10
Несвободное твёрдое тело
Твёрдое тело, на перемещение которого не наложено никаких ограничений, называется свободным. Тело, ограничивающее свободу движения данного твёрдого тела, является по отношению к нему связью. Твёрдое тело, свобода движения которого ограничена связями, называется несвободным. Всякое связанное тело можно представить свободным, если связи заменить их реакциями (принцип освобождаемости твёрдых тел от связей). Все связи можно разделить на несколько типов. 1. Идеально гладкая поверхность.
Рис. 1.11 Реакции опоры, приложены в точке опоры, всегда направлены перпендикулярно опоре. 2. Гибкая связь (трос, нить, цепь, канат)
Рис. 1.12 Реакция гибкой нити, направлена на нити к точке подвеса. 3. Жёсткий стержень На схемах показывается толстой линией. Реакция стержня направлена вдоль стержня. Стержень может быть сжат или растянут. Точное направление реакции определяют, мысленно убрав стержень и анализируя направление перемещение узла.
Рис. 1.13
4. Брус.
Рис. 1.14
5. Цилиндрическая шарнирно – неподвижная опора
Рис. 1.15
6. Цилиндрическая шарнирно – подвижная опора
Рис. 1.16
7. Защемление (заделка)
Рис. 1.17
8. Невесомый стержень, на концах которого шарниры
Рис. 1.18 9. Сферический шарнир
Рис. 1.19
10. Подпятник (Совокупность цилиндрического шарнира и упорной поверхности)
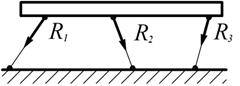
Рис. 1.20 ПЛОСКАЯ СИСТЕМА СИЛ Система сходящихся сил 2.1.1 Равновесие твёрдого тела, к которому приложена система сходящихся сил. Сходящимися называются силы, линии, действия которых пересекаются в одной точке. Теорема. Система сходящихся сил эквивалентна общей силе, равнодействующей, которая равна геометрической сумме этих сил и проходит через точку пересечения их линий действия.
Согласно следствию из аксиомы 3 перенесём точки приложения сил по линиям их действия в точку пересечения этих линий. Она эквивалентна исходной системе сходящихся сил. Равнодействующую двух пересекающихся сил можно определить с помощью параллелограмма (4 аксиома).
Рис. 1.21
Равнодействующая
Рис. 1.22 Строим силовой многоугольник: от конца
Рис. 1.23 Обе части (1) спроектируем на оси x, y,z.
Модуль равнодействующей
Направление равнодействующей определяется направляющимися косинусами
где i, j, k – единичные орты осей x, y, z. Для равновесия твёрдого тела, к которому приложена система сходящихся сил, необходимо и достаточно, чтобы векторная сумма этих сил равнялась нулю: Это означает, что в силовом многоугольнике уравновешенной системе сходящихся сил конец последней силы должен совпадать с началом первой, то есть многоугольник замкнут.
Рис. 1.24 Равенство
Для равновесия системы сходящихся сил необходимо и достаточно, чтобы алгебраические проекции всех сил данной системы на координаты осей x, y, z равнялись нулю. Для плоской системы сходящихся сил система принимает вид:
2.1.2. Теорема о трех не параллельных силах. Если исходное тело находится в равновесии под действием трех не параллельных сил, лежащих в одной плоскости, то лини действия этих сил пересекаются в одной точке. Доказательство: Пусть на тело действует система трех сил
Рис. 1.25 Таким образом, рассматриваемая система сил приведена к двум 2.1.3. Момент силы относительно точки. Опыт показывает, что под действием силы твёрдое тело может наряду с поступательным перемещением совершать вращение вокруг того или иного центра. Вращательный эффект силы характеризуется её моментом. Моментом силы относительно центра называется вектор равный векторному произведению радиуса – вектора точки приложения силы на вектор силы.
Рис. 1.26 Вектор – момент силы Модуль векторного произведения равен площади параллелограмма построенного на векторных сомножителей. Его модуль равен
В общем случае, момент силы относительно центра алгебраически равен взятому со знаком “+” или “-” произведению модуля силы на плечо силы.
Знак “+” выбираем в том случае, если кратчайший поворот силы вокруг данного центра виден происходящим против часовой стрелки.
Рис. 1.27 Момент силы относительно точки равен нулю, если линия действия силы проходит через эту точку, так как при этом плечо равно нулю. 2.1.4. Теорема Вариньона Теорема Вариньона для системы сходящихся сил гласит: момент относительно точки равнодействующей
Удобство данной теоремы заключается в том, что, минуя непосредственное определение равнодействующей, можно вычислить её момент относительно точки, зная моменты всех слагаемых сил относительно той же точки.
Рис. 1.28
где x, y – координаты точки В. Этой формулой рекомендуется пользоваться в тех случаях, когда определение величины h связано с вычислительными трудностями. Системы сходящихся сил.
В отличии от соответственно плоской задачи, силовой многоугольник не является плоским, то есть он представляет ломаную пространственную линию. Проекции равнодействующей силы R на оси декартовых координат x, y, z равны суммам проекций слагаемых сил на соответствующей оси.
Рис. 1.38
Модуль равнодействующей R:
Направляющие косинусы равны:
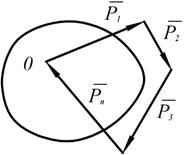
Рис. 1.39 Для равновесия твердого тела, к которому приложена пространственная система сходящихся сил, необходимо и достаточно, чтобы равнодействующая равнялась нулю, то есть, чтобы силовой многоугольник был замкнут. При этом уравнения равновесия имеют вид:
ЦЕНТР ТЯЖЕСТИ. Сила тяжести – равнодействующая сил притяжения к Земле, она распределена по всему объёму тела. Силы притяжения, приложенные к частицам твёрдого тела, образуют систему сил, линии, действия которых сходятся в центре Земли. Поскольку радиус Земли значительно больше размеров любого земного тела, силы притяжения можно считать параллельными.
Рис. 1.48 Для определения точки приложения силы тяжести (равнодействующей параллельных сил) используем теорему Вариньона о моменте равнодействующей: Момент равнодействующей относительно оси равен алгебраической сумме моментов сил системы относительно этой оси. Изображаем тело, составленное из нескольких частей Пусть равнодействующая (сила тяжести всего тела) – приложена в неизвестном пока центре
Рис. 1.49 Из теоремы Вариньона следует:
В однородном теле сила тяжести пропорциональна объёму
Следовательно, в формулах для однородных тел:
Центр тяжести однородных плоских тел (плоских фигур). Для плоских тел можно записать:
Тогда после подстановки в записанные выше формулы получим
Выражение Аналогично Тогда координаты центра тяжести сечения можно выразить:
Оси, проходящие через центр тяжести, называются центральными. Статический момент относительно центральной оси равен нулю. Положение центра тяжести простых геометрических фигур:
Рис.1.50 При решении задач необходимо учесть: 1. Центр тяжести симметричных фигур находятся на оси симметрии. 2. Сложные сечения разделяем на несколько простых. 3. Полости (отверстия)рассматриваются как часть сечения с отрицательной площадью. Пример. Необходимо определить центр тяжести представленного сечения.
Рис.1.51 Разбиваем сечение на простейшие геометрические фигуры (прямоугольник, треугольник, половина круга). Площадь прямоугольника
Площадь треугольника
Площадь половины круга
Центр тяжести:
прямоугольника
треугольника
половины круга
Положение центра тяжести, представленного сечения определяем по формуле
РАЗДЕЛ ВТОРОЙ КИНЕМАТИКА. 1. ВВЕДЕНИЕ
Кинематикой называется раздел механики, в котором изучается движение материальных точек и тел в пространстве с геометрической точки зрения, вне связи с силами, определяющими это движение. Мы будем изучать простейшую форму движения – механическое движение, то есть происходящее во времени изменение положения одного тела относительно другого, с которым связана система координат, называемая системой отсчета. Эта система может быть как движущейся, так и условно неподвижной. Рассматривая движение, мы связываем изменение положения тела с течением времени. При изучении движения всегда устанавливаем начало отсчета времени Непрерывную кривую, которую описывает точка при своем движении, называют траекторией. Если траектория движения – прямая линия, то движение называется прямолинейным, если кривая – криволинейным.
ДВИЖЕНИЕ ТОЧКИ. 2.1. Способ задания движения. Задать движение точки по отношению к избранной системе отсчета – это значит указать способ, при помощи которого можно определить положение точки в любой момент времени. Существуют три способа задания движения: 1. Векторный способ.
Для определения движения точки нужно знать, как изменяется с течением времени
Рис. 2.1
Годографом какого-либо вектора называют кривую, которую вычерчивает конец этого вектора при изменении его аргумента (предполагается, что начало вектора, находится в одной и той же точке). Таким образом, годографом радиус – вектора является траектория точки. 2. Координатный способ.
При движении точки М ее координаты изменяются с течением времени. Следовательно, координаты х, y, z движущейся точки, являются функциями времени
Рис. 2.2
Эти уравнения называются уравнениями движения точки в декартовых координатах. Пусть движение точки М в плоскости задано уравнениями:
Из первого уравнения выразим время 3. Естественный способ задания движения. Этот способ применяется в том случае, если траектория точки заранее известна. Выберем на траектории неподвижную точку О, которую назовем началом отсчета дуговой координаты. Рис. 2.3 направление отсчета дуговой координаты. При движении точки М расстояние S от этой точки до неподвижной точки О изменяется с течением времени:
2.2. Скорость точки. 1. Векторный способ задания движения. Пусть в момент времени
Рис. 2.4
Вектор
Скоростью точки в данный момент времени называется предел отношения вектора перемещения точки к промежутку времени, за которое произошло это перемещение, при стремлении этого промежутка времени к нулю
Скорость точки – это вектор, направленный по касательной к траектории в сторону движения. 2. Координатный способ задания движения. Пусть движение точки задано
Тогда для радиуса – вектора точки М можно записать
где Согласно (5) Дифференцируем (*)
С другой стороны для вектора
где Сравнивая (**) и (***), получим
Модуль скорости точки
Направление скорости определяется направляющими косинусами:
3. Естественный способ задания движения. Пусть в момент времени t положение точки М определяется координатой S, в момент Согласно (5)
Вычислим модуль и определим направление
Вектор
Рис. 2.5 При Обозначим единичный орт касательной через
Таким образом Равенство (*) примет вид:
Модуль
2.3. Ускорение точки. 1. При векторном способе задания движения. Предположим, что в момент времени Предел приращения скорости к приращению времени за которое произошло это приращение, при условии, что
2. При координатном способе задания движения. Вектор скорости точки
С учетом (9)
Но для вектора ускорения точки имеем
Сравнивая (*) и (**), получим
Модуль ускорения точки
Направление вектора ускорения определяется направляющими косинусами:
3. При естественном способе задания движения. Пусть известна траектория точки. Возьмем две близкие на траектории точки М и М1 – Вектор Плоскость перпендикулярная соприкасающейся, называется нормальной плоскостью. Плоскость перпендикулярная нормальной и соприкасающейся плоскостям называется спрямляющей плоскостью.
Рис.2.6 Три взаимно перпендикулярные плоскости: нормальная, соприкасающая и спрямляющая образуют естественный трехгранник. Линия пересечения нормальной и соприкасающейся плоскостей называется главной нормалью. Орт главной нормали – Три взаимно перпендикулярные оси: касательная, направленная в сторону возрастания дуговой координаты; главная нормаль, направленная в сторону вогнутости траектории; бинормаль, направленная по отношению к Угол между касательными в двух ближайших точках траектории называется углом смежности Кривизной кривой в точке М называется предел отношения угла смежности к абсолютному значению длины дуги ММ, между ближайшими точками траектории
Радиусом кривизны в точке М называется величина, обратная кривизне:
Получим формулу для вычисления ускорения точки М. Согласно выражению (8) имеем:
Продифференцируем по времени обе части этого равенства
Вычислим
Так как направление по главной нормали, то Подставим в (*)
Ускорение точки лежит в соприкасающейся плоскости и определяется как векторная сумма касательного и нормального ускорений точки:
Проекция ускорения на касате
|
|||||||
|
Последнее изменение этой страницы: 2016-09-13; просмотров: 626; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.135.193.166 (0.012 с.) |


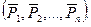
 можно заменить другой системой
можно заменить другой системой  и наоборот, то такие системы сил называются эквивалентными
и наоборот, то такие системы сил называются эквивалентными .
. эквивалентна одной силе
эквивалентна одной силе 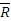 , то есть
, то есть  , то последняя называется равнодействующей этой системы сил.
, то последняя называется равнодействующей этой системы сил.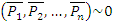
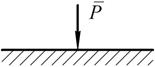

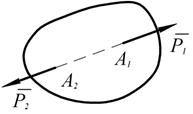

 , под действием которых тело находится в покое или совершает какое-то движение. Приложим к телу равные противоположно направленные силы
, под действием которых тело находится в покое или совершает какое-то движение. Приложим к телу равные противоположно направленные силы  и
и  , которые взаимно уравновешиваются.
, которые взаимно уравновешиваются.  Если тело находится в движении, то оно будет двигаться под действием новой системы сил
Если тело находится в движении, то оно будет двигаться под действием новой системы сил  так же и под действием сил
так же и под действием сил  , то есть основная система сил эквивалентна прежней.
, то есть основная система сил эквивалентна прежней.
 . Приложим в точке В две силы
. Приложим в точке В две силы  и
и  равные по модулю силе
равные по модулю силе  Равнодействующая двух пересекающихся сил приложена в точке их пересечения и изображается диагональю параллелограмма, построенного на этих силах.
Равнодействующая двух пересекающихся сил приложена в точке их пересечения и изображается диагональю параллелограмма, построенного на этих силах.









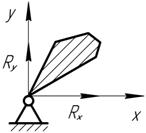






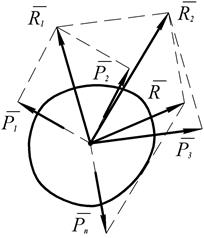

 (1)
(1)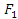 отложим
отложим  от его конца
от его конца 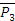 и так далее. Затем соединить начало первого вектора с концом последнего. Последний вектор и есть
и так далее. Затем соединить начало первого вектора с концом последнего. Последний вектор и есть 


 (2)
(2)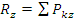
 (3)
(3)
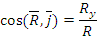

 (*)
(*)



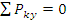 (4)
(4) или
или 
 , причём линии действия
, причём линии действия 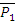 и
и  пересекаются в точке А, согласно аксиоме 4 их можно заменить одной
пересекаются в точке А, согласно аксиоме 4 их можно заменить одной 

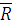 и
и 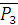 . По условиям теоремы тело находится в равновесии, следовательно, по аксиоме 2 силы
. По условиям теоремы тело находится в равновесии, следовательно, по аксиоме 2 силы  (6)
(6)
 относительно точки О приложен в т. О
относительно точки О приложен в т. О ,
,


 равен сумме моментов слагаемых сил относительно той же точки:
равен сумме моментов слагаемых сил относительно той же точки: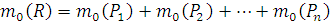

 – координаты точки А.
– координаты точки А.
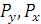 – проекции силы
– проекции силы  на координатные оси,
на координатные оси, Равнодействующую пространственной системы сил можно определить, построив пространственный многоугольник.
Равнодействующую пространственной системы сил можно определить, построив пространственный многоугольник.

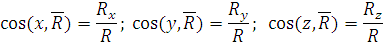

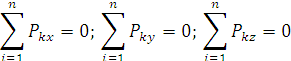

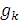 - силы тяжести частей, приложены в центрах тяжести частей.
- силы тяжести частей, приложены в центрах тяжести частей. .
. – координаты центра тяжести
– координаты центра тяжести  – координаты центров тяжести частей тела.
– координаты центров тяжести частей тела.



 :
: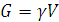 ,
, – вес единицы объёма
– вес единицы объёма


 – объём элемента тела
– объём элемента тела , где
, где  – площадь фигуры,
– площадь фигуры, 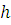 – её высота.
– её высота.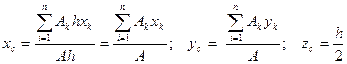
 – площадь части сечения
– площадь части сечения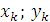 – координаты центра тяжести частей сечения
– координаты центра тяжести частей сечения – называют статическим моментом площади
– называют статическим моментом площади  относительно оси y.
относительно оси y.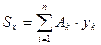 – статический момент относительно оси х.
– статический момент относительно оси х.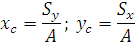







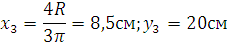
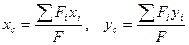 .
.
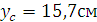 .
. .
. Положение точки в пространстве однозначно определенном заданием радиуса – вектора
Положение точки в пространстве однозначно определенном заданием радиуса – вектора  , проведенного из некоторого неподвижного центра О в данную точку М.
, проведенного из некоторого неподвижного центра О в данную точку М. . (1)
. (1) Положение точки М в системе координат ОХУ определяется координатами х, y, z.
Положение точки М в системе координат ОХУ определяется координатами х, y, z. (2)
(2)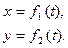
 и подставим во второе:
и подставим во второе: 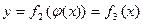 – полученная зависимость есть уравнение траектории точки.
– полученная зависимость есть уравнение траектории точки. Положение точки М на траектории будем определять дуговой координатой S, отложенной на траектории от начала отсчета О. Расстояния, отложенные в одну сторону от точки О, будем считать положительными, в другую – отрицательными, то есть установим
Положение точки М на траектории будем определять дуговой координатой S, отложенной на траектории от начала отсчета О. Расстояния, отложенные в одну сторону от точки О, будем считать положительными, в другую – отрицательными, то есть установим – уравнение движения т. М (3)
– уравнение движения т. М (3)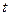 положение точки М определяется
положение точки М определяется  , а в момент
, а в момент  .
.
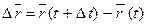 будем называть вектором перемещения точки за время
будем называть вектором перемещения точки за время  . Отношение
. Отношение  к
к  (4)
(4) (5)
(5)

 , (*)
, (*) – единицы орты осей х, y, z.
– единицы орты осей х, y, z.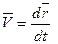 .
. . (**)
. (**) справедливо соотношение
справедливо соотношение , (***)
, (***)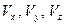 – проекции
– проекции  (6)
(6) (7)
(7)
 –
– 

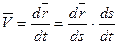 (*)
(*) :
:

 направлен так же, как
направлен так же, как 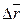 .
.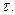
 ,
, , следовательно
, следовательно 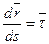 , так как
, так как  .
. (8)
(8) , направление
, направление  .
. , а в момент
, а в момент  .
. (9)
(9) .
. (*)
(*) (**)
(**)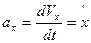
 (10)
(10)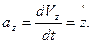
 . (11)
. (11)
 .
. перенесем в точку М и проведем плоскость через
перенесем в точку М и проведем плоскость через 
 . Линия пересечения нормальной и спрямляющей плоскостей называется бинормалью траектории. Ось бинормали
. Линия пересечения нормальной и спрямляющей плоскостей называется бинормалью траектории. Ось бинормали 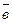 .
.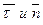 также, как ось z по отношению к осям х, y, называются естественными осями.
также, как ось z по отношению к осям х, y, называются естественными осями. .
.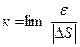 (12)
(12)
 . (13)
. (13)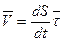 .
. (*)
(*) .
. 
 .
. ,
, . (14)
. (14)


