
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Произвольная пространственная система сил.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
3.2.1. Момент силы относительно точки. Момент силы относительно оси. Теория пар в пространстве. В случае плоской системы сил момент силы относительно точки определён как алгебраическая величина:
Рис. 1.40
Модуль вектора
Моментом силы относительно оси называется скалярная величина, равная моменту проекции этой силы на плоскость, перпендикулярную оси, взятому относительно точки пересечения оси с плоскостью.
Рис. 1.41
Если сила Итак, момент силы относительно точки – вектор, а момент силы относительно оси – скалярная величина. При вычислении моментов относительно оси надо иметь следующие частные случаи: 1. Если сила параллельна оси, то её момент относительно оси равен нулю 2. Если линия действия силы пересекает ось, то её момент относительно оси равен нулю 3. Если сила перпендикулярна оси, то её момент относительно оси равен произведению модуля силы на расстояние между силой и осью. Получим аналитическое выражение для моментов силы относительно осей координат.
Рис. 1.42 Спроецируем силу
Последнее равенство вытекает из теоремы Вариньона. Но как видно из чертежа, В результате получим:
3.2.2. Зависимость между моментом силы относительно центра и относительно оси.
Рис. 1.43 Пусть на тело действует приложенная в точке
Проведём теперь через любую точку
Но треугольник Тогда Умножим обе части уравнения на 2, находим
Так как произведение Момент силы
3.3.3. Главные векторы сил и моментов. Главным вектором системы сил называется геометрическая сумма сил системы.
Рассмотрим систему сил, как угодно ориентированных в пространстве. Вычислим моменты этих сил относительно точки
Векторы
Рис. 1.44
Таким образом, главным моментом пространственной системы сил относительно центра называется геометрическая сумма моментов сил системы относительно того же центра. Главным моментом пространственной системы сил относительно неподвижной оси называется алгебраическая сумма моментов сил системы той же оси.
3.2.4. Приведение пространственной системы сил к заданному центру. Приведение силы к заданному центру (метод Пуансо).
Рис. 1.45
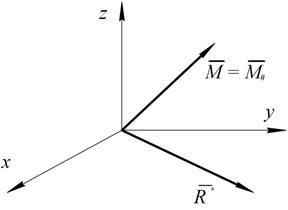
Приведём силу к центру Силы При приведении сил к заданному центру получаем в этом центре силу, геометрически равную заданной, и пару, момент которой равен моменту силы относительно центра приведения. Теорема При приведении пространственной системы сил к центру всегда получим силу, называемую главным вектором сил, приложенную в центре приведения и пару сил, момент которой равен главному моменту системы сил относительно центра приведения.
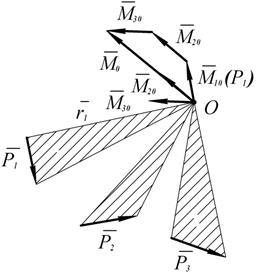
Пусть имеем систему сил, как угодно ориентированных в пространстве (ограничимся тремя силами). Каждую силу приводим к центру Векторы моментов
Рис. 1.46 так же образуют систему, сходящихся векторов. Их геометрическая сумма – есть главный момент системы сил относительно центра 3.2.5. Вычисление главного вектора и главного момента пространственной системы сил. Главный вектор:
Спроектируем обе части этого векторного соотношения на оси
Тогда модуль
Направление
Рис. 1.47
Главный момент
Спроектируем данное векторное соотношение на оси
Модуль главного момента равен
Направление определяем направлением косинусов:
3.2.6. Условия и уравнения равновесия пространственной системы сил. Теорема Для равновесия пространственной системы сил необходимо и достаточно, чтобы главный вектор и главный момент равнялись нулю. Доказательство: Достаточность. При Необходимость. Пусть данная система сил эквивалентна нулю. Тогда необходимо, чтобы Если какое-либо из этих условий не выполняется, то система сил приводится либо Уравнения равновесия:
В случае произвольной пространственной системы сил задача является статически определенной, если число алгебраических неизвестных не более шести. ЦЕНТР ТЯЖЕСТИ. Сила тяжести – равнодействующая сил притяжения к Земле, она распределена по всему объёму тела. Силы притяжения, приложенные к частицам твёрдого тела, образуют систему сил, линии, действия которых сходятся в центре Земли. Поскольку радиус Земли значительно больше размеров любого земного тела, силы притяжения можно считать параллельными.
Рис. 1.48 Для определения точки приложения силы тяжести (равнодействующей параллельных сил) используем теорему Вариньона о моменте равнодействующей: Момент равнодействующей относительно оси равен алгебраической сумме моментов сил системы относительно этой оси. Изображаем тело, составленное из нескольких частей Пусть равнодействующая (сила тяжести всего тела) – приложена в неизвестном пока центре
Рис. 1.49 Из теоремы Вариньона следует:
В однородном теле сила тяжести пропорциональна объёму
Следовательно, в формулах для однородных тел:
Центр тяжести однородных плоских тел (плоских фигур). Для плоских тел можно записать:
Тогда после подстановки в записанные выше формулы получим
Выражение Аналогично Тогда координаты центра тяжести сечения можно выразить:
Оси, проходящие через центр тяжести, называются центральными. Статический момент относительно центральной оси равен нулю. Положение центра тяжести простых геометрических фигур:
Рис.1.50 При решении задач необходимо учесть: 1. Центр тяжести симметричных фигур находятся на оси симметрии. 2. Сложные сечения разделяем на несколько простых. 3. Полости (отверстия)рассматриваются как часть сечения с отрицательной площадью. Пример. Необходимо определить центр тяжести представленного сечения.
Рис.1.51 Разбиваем сечение на простейшие геометрические фигуры (прямоугольник, треугольник, половина круга). Площадь прямоугольника
Площадь треугольника
Площадь половины круга
Центр тяжести:
прямоугольника
треугольника
половины круга
Положение центра тяжести, представленного сечения определяем по формуле
РАЗДЕЛ ВТОРОЙ КИНЕМАТИКА. 1. ВВЕДЕНИЕ
Кинематикой называется раздел механики, в котором изучается движение материальных точек и тел в пространстве с геометрической точки зрения, вне связи с силами, определяющими это движение. Мы будем изучать простейшую форму движения – механическое движение, то есть происходящее во времени изменение положения одного тела относительно другого, с которым связана система координат, называемая системой отсчета. Эта система может быть как движущейся, так и условно неподвижной. Рассматривая движение, мы связываем изменение положения тела с течением времени. При изучении движения всегда устанавливаем начало отсчета времени Непрерывную кривую, которую описывает точка при своем движении, называют траекторией. Если траектория движения – прямая линия, то движение называется прямолинейным, если кривая – криволинейным.
ДВИЖЕНИЕ ТОЧКИ. 2.1. Способ задания движения. Задать движение точки по отношению к избранной системе отсчета – это значит указать способ, при помощи которого можно определить положение точки в любой момент времени. Существуют три способа задания движения: 1. Векторный способ.
Для определения движения точки нужно знать, как изменяется с течением времени
Рис. 2.1
Годографом какого-либо вектора называют кривую, которую вычерчивает конец этого вектора при изменении его аргумента (предполагается, что начало вектора, находится в одной и той же точке). Таким образом, годографом радиус – вектора является траектория точки. 2. Координатный способ.
При движении точки М ее координаты изменяются с течением времени. Следовательно, координаты х, y, z движущейся точки, являются функциями времени
Рис. 2.2
Эти уравнения называются уравнениями движения точки в декартовых координатах. Пусть движение точки М в плоскости задано уравнениями:
Из первого уравнения выразим время 3. Естественный способ задания движения. Этот способ применяется в том случае, если траектория точки заранее известна. Выберем на траектории неподвижную точку О, которую назовем началом отсчета дуговой координаты. Рис. 2.3 направление отсчета дуговой координаты. При движении точки М расстояние S от этой точки до неподвижной точки О изменяется с течением времени:
2.2. Скорость точки. 1. Векторный способ задания движения. Пусть в момент времени
Рис. 2.4
Вектор
Скоростью точки в данный момент времени называется предел отношения вектора перемещения точки к промежутку времени, за которое произошло это перемещение, при стремлении этого промежутка времени к нулю
Скорость точки – это вектор, направленный по касательной к траектории в сторону движения. 2. Координатный способ задания движения. Пусть движение точки задано
Тогда для радиуса – вектора точки М можно записать
где Согласно (5) Дифференцируем (*)
С другой стороны для вектора
где Сравнивая (**) и (***), получим
Модуль скорости точки
Направление скорости определяется направляющими косинусами:
3. Естественный способ задания движения. Пусть в момент времени t положение точки М определяется координатой S, в момент Согласно (5)
Вычислим модуль и определим направление
Вектор
Рис. 2.5 При Обозначим единичный орт касательной через
Таким образом Равенство (*) примет вид:
Модуль
2.3. Ускорение точки. 1. При векторном способе задания движения. Предположим, что в момент времени Предел приращения скорости к приращению времени за которое произошло это приращение, при условии, что
2. При координатном способе задания движения. Вектор скорости точки
С учетом (9)
Но для вектора ускорения точки имеем
Сравнивая (*) и (**), получим
Модуль ускорения точки
Направление вектора ускорения определяется направляющими косинусами:
3. При естественном способе задания движения. Пусть известна траектория точки. Возьмем две близкие на траектории точки М и М1 – Вектор Плоскость перпендикулярная соприкасающейся, называется нормальной плоскостью. Плоскость перпендикулярная нормальной и соприкасающейся плоскостям называется спрямляющей плоскостью.
Рис.2.6 Три взаимно перпендикулярные плоскости: нормальная, соприкасающая и спрямляющая образуют естественный трехгранник. Линия пересечения нормальной и соприкасающейся плоскостей называется главной нормалью. Орт главной нормали – Три взаимно перпендикулярные оси: касательная, направленная в сторону возрастания дуговой координаты; главная нормаль, направленная в сторону вогнутости траектории; бинормаль, направленная по отношению к Угол между касательными в двух ближайших точках траектории называется углом смежности Кривизной кривой в точке М называется предел отношения угла смежности к абсолютному значению длины дуги ММ, между ближайшими точками траектории
Радиусом кривизны в точке М называется величина, обратная кривизне:
Получим формулу для вычисления ускорения точки М. Согласно выражению (8) имеем:
Продифференцируем по времени обе части этого равенства
Вычислим
Так как направление по главной нормали, то Подставим в (*)
Ускорение точки лежит в соприкасающейся плоскости и определяется как векторная сумма касательного и нормального ускорений точки:
Проекция ускорения на касательную определяется формулой:
Касательное ускорение характеризует изменение скорости по величине. Оно равно нулю, когда величина скорости остается неизменной. Кроме того, оно обращается в нуль в те моменты времени, когда скорость достигает экстремальных значений. Величина нормального ускорения определяется формулой:
где Нормальное ускорение характеризует изменение скорости по направлению. Оно равно нулю при прямолинейном движении точки, а также в точках перегиба траектории, так как в обоих случаях радиус кривизны обращается в бесконечность. Кроме того,
Рис. 2.7
Направление ускорения: Некоторые частные случаи движения точки. 1. Прямолинейное движение
Так как при прямолинейном движении скорость изменяется только численно, то делаем вывод, что касательное ускорение характеризует изменение скорости по численной величине. 2. Равномерное криволинейное движение Равномерным называется такое движение, в котором численная величина скорости остается все время постоянной (
Так как ускорение при равномерном движении появляется в результате изменения направления скорости, то нормальное ускорение характеризует изменение скорости по направлению. Получим закон движения.
Отсюда: Проинтегрируем: Подставим пределы интегрирования: В результате получим закон равномерного криволинейного движения:
3. Равномерное прямолинейное движение
следовательно, 4. Равнопеременное криволинейное движение Равнопеременным называется такое криволинейное движение, при котором касательное ускорение остается величиной постоянной:
но
|
||||
|
Последнее изменение этой страницы: 2016-09-13; просмотров: 795; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.144.162 (0.009 с.) |

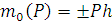 . При пространственном расположении сил этого определения не достаточно, так как плоскости, проходящие через линии действия сил и точку, относительно которой определяется момент, различны. Поэтому момент
. При пространственном расположении сил этого определения не достаточно, так как плоскости, проходящие через линии действия сил и точку, относительно которой определяется момент, различны. Поэтому момент  силы P относительно точки О в пространстве определяют как векторное произведение
силы P относительно точки О в пространстве определяют как векторное произведение  , где
, где 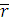 - вектор радиус проведенный из точки О в точку приложения силы.
- вектор радиус проведенный из точки О в точку приложения силы.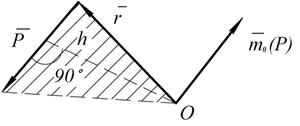 Таким образом вектор
Таким образом вектор  направлен перпендикулярно плоскости, содержащий линию действия силы и точку О, так что сила
направлен перпендикулярно плоскости, содержащий линию действия силы и точку О, так что сила 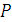 с конца его вектора
с конца его вектора 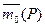 равен:
равен:


 с конца оси z видно направление вокруг точки О против часовой стрелки то момент положительный.
с конца оси z видно направление вокруг точки О против часовой стрелки то момент положительный. .
. .
.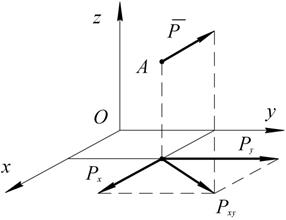
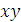 и разложим полученную проекцию на составляющие
и разложим полученную проекцию на составляющие  и
и 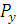 ; численно эти составляющие будут, очевидно, равны проекциям силы
; численно эти составляющие будут, очевидно, равны проекциям силы  на оси
на оси 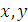 . Тогда
. Тогда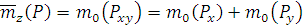
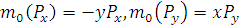 следовательно
следовательно  . Аналогично вычисляются моменты относительно других осей.
. Аналогично вычисляются моменты относительно других осей.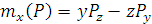
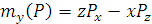

 сила
сила  и возьмем на ней произвольную точку
и возьмем на ней произвольную точку 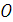 . момент силы
. момент силы  , перпендикулярным плоскости
, перпендикулярным плоскости  , причём по модулю
, причём по модулю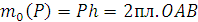 .
.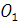 плоскость
плоскость 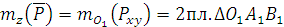
 представляет собой проекцию треугольника
представляет собой проекцию треугольника  .
.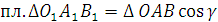 .
.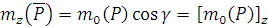
 даёт проекцию
даёт проекцию  или
или  .
.
 .
.

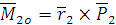
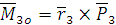

 все приложены в точке
все приложены в точке 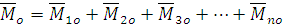
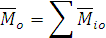
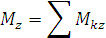

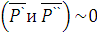 , причём
, причём 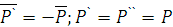
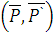 образуют пару, момент которой
образуют пару, момент которой 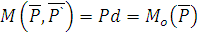 .
.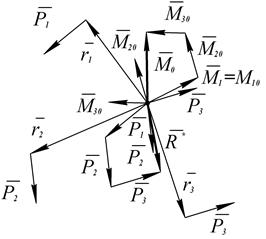 Доказательство:
Доказательство: . Геометрическая сумма этих сил – есть главный вектор:
. Геометрическая сумма этих сил – есть главный вектор: 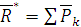 .
.
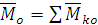 .
. .
.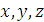 .
.
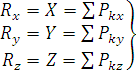
 равен:
равен: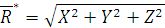


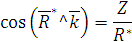
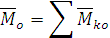
 :
:


 , система сходящихся сил, приложенных в центре приведения эквивалентна нулю, а при
, система сходящихся сил, приложенных в центре приведения эквивалентна нулю, а при 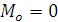 - система пар сил эквивалентна нулю. Следовательно, исходная система сил эквивалентна нулю.
- система пар сил эквивалентна нулю. Следовательно, исходная система сил эквивалентна нулю. .
.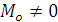 и следовательно, не является уравновешенной, что противоречит исходной предпосылке.
и следовательно, не является уравновешенной, что противоречит исходной предпосылке.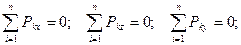
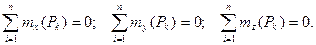

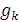 - силы тяжести частей, приложены в центрах тяжести частей.
- силы тяжести частей, приложены в центрах тяжести частей. .
. – координаты центра тяжести
– координаты центра тяжести  – координаты центров тяжести частей тела.
– координаты центров тяжести частей тела.



 :
: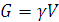 ,
,


 – объём элемента тела
– объём элемента тела , где
, где 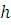 – её высота.
– её высота.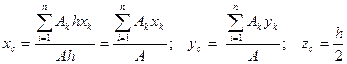
 – площадь части сечения
– площадь части сечения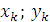 – координаты центра тяжести частей сечения
– координаты центра тяжести частей сечения – называют статическим моментом площади
– называют статическим моментом площади  относительно оси y.
относительно оси y.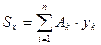 – статический момент относительно оси х.
– статический момент относительно оси х.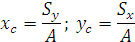







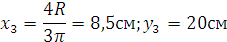
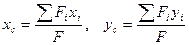 .
.
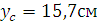 .
. .
. Положение точки в пространстве однозначно определенном заданием радиуса – вектора
Положение точки в пространстве однозначно определенном заданием радиуса – вектора  , проведенного из некоторого неподвижного центра О в данную точку М.
, проведенного из некоторого неподвижного центра О в данную точку М. . (1)
. (1) Положение точки М в системе координат ОХУ определяется координатами х, y, z.
Положение точки М в системе координат ОХУ определяется координатами х, y, z. (2)
(2)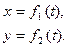
 и подставим во второе:
и подставим во второе: 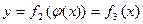 – полученная зависимость есть уравнение траектории точки.
– полученная зависимость есть уравнение траектории точки. Положение точки М на траектории будем определять дуговой координатой S, отложенной на траектории от начала отсчета О. Расстояния, отложенные в одну сторону от точки О, будем считать положительными, в другую – отрицательными, то есть установим
Положение точки М на траектории будем определять дуговой координатой S, отложенной на траектории от начала отсчета О. Расстояния, отложенные в одну сторону от точки О, будем считать положительными, в другую – отрицательными, то есть установим – уравнение движения т. М (3)
– уравнение движения т. М (3)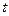 положение точки М определяется
положение точки М определяется  , а в момент
, а в момент  .
.
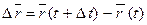 будем называть вектором перемещения точки за время
будем называть вектором перемещения точки за время  . Отношение
. Отношение  к
к  (4)
(4) (5)
(5)

 , (*)
, (*) – единицы орты осей х, y, z.
– единицы орты осей х, y, z.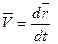 .
. . (**)
. (**) справедливо соотношение
справедливо соотношение , (***)
, (***)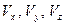 – проекции
– проекции  (6)
(6) (7)
(7)
 –
– 

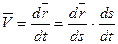 (*)
(*) :
:

 направлен так же, как
направлен так же, как 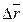 .
.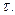
 ,
, , следовательно
, следовательно 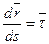 , так как
, так как  .
. (8)
(8) , направление
, направление  .
. , а в момент
, а в момент  .
. (9)
(9) .
. (*)
(*) (**)
(**)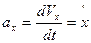
 (10)
(10)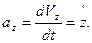
 . (11)
. (11)
 .
. перенесем в точку М и проведем плоскость через
перенесем в точку М и проведем плоскость через 
 . Линия пересечения нормальной и спрямляющей плоскостей называется бинормалью траектории. Ось бинормали
. Линия пересечения нормальной и спрямляющей плоскостей называется бинормалью траектории. Ось бинормали 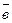 .
.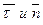 также, как ось z по отношению к осям х, y, называются естественными осями.
также, как ось z по отношению к осям х, y, называются естественными осями. .
.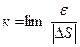 (12)
(12)
 . (13)
. (13)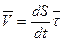 .
. (*)
(*) .
. 
 .
. ,
, . (14)
. (14)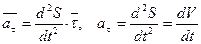 . (15)
. (15)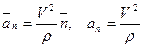 , (16)
, (16) – радиус кривизны.
– радиус кривизны. в точках где V=0.
в точках где V=0.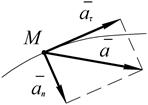 Модуль ускорения вычисляется по формуле:
Модуль ускорения вычисляется по формуле: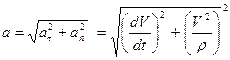 . (16)
. (16)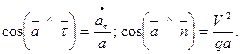
 .
. ):
):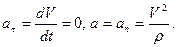
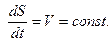
 .
.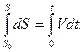
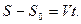
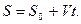
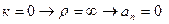
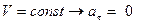
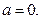
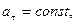
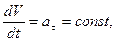
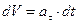 , проинтегрируем
, проинтегрируем
 проинтегрируем
проинтегрируем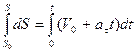
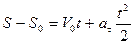
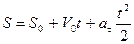 – закон равнопеременного криволинейного движения.
– закон равнопеременного криволинейного движения.


