
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Потенциальное силовое поле и силовая функция.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Работа на перемещение
Вычислить данный интеграл, не зная происходящего движения (то есть зависимостей x, y,z от времени t) можно лишь в случае, когда сила зависит только от положения точки, то есть её координат x, y,z. Про такие силы говорят, что они образуют силовое поле. Силовым полем называется часть пространства, в каждой точке которого на помещённую материальную частицу действует определённая по модулю и направлению сила, зависящая от положения частицы. Примером силового поля служит поле тяготения планеты или Солнца. Так как, сила определяющая её проекции на оси координат то силовое поле задаётся уравнениями:
Однако, если окажется что выражение стоящее в формуле (1) под знаком интеграла и представляющее собой элементарную работу силы, будет полным дифференциалом некоторой функции
Функция,
Силы, работа которых зависит от вида траектории или от закона движения точки приложенной силы – не потенциальным (сила трения и сопротивления среды). Примером потенциальных сил являются сила тяжести, упругая сила и сила тяготения. – для силы тяжести, если ось z верх
– для упругой силы, действующей вдоль оси Ox – для силы тяготения
Потенциальная энергия
Для потенциальных сил можно вывести понятие о потенциальной энергии, как о величине, «характеризующей запас работы», которым обладает материальная точка в данном пункте силового поля. Потенциальной энергией материальной точки в данном положении М называется скалярная величина П, равная той же работе, которую произведут силы поля при перемещении точки из положения М в нулевое:
Будем считать нулевое значение точки для функции U – значение силовой функции в точке М поля Отсюда
то есть потенциальная энергия в любой точке равна значению силовой функции в этой точке, взятому с обратным знаком. Отсюда видно, что вместо силовой функции можно пользоваться понятием о потенциальной энергии. В частности работу потенциальной силы (34) можно вычислять по формуле
Работа потенциальной силы равна разности значений потенциальной энергии движущейся точки в начальном и конечном её положениях. Закон сохранения механической энергии Допустим, что все действующие на систему внешние и внутренние силы потенциальны. Тогда для каждой из точек системы работа приложенных сил равна:
Следовательно, для всех внешних и внутренних сил:
Подставим это выражение работы, в уравнение (
или
Следовательно, при движении под действием потенциальных сил сумма кинетической и потенциальной энергий системы в каждом её положении остаётся величиной постоянной.
ОГЛАВЛЕНИЕ
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-13; просмотров: 456; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.186.62 (0.011 с.) |

 силы F приложенной в точке
силы F приложенной в точке  вычисляется по формуле
вычисляется по формуле (33)
(33) (34)
(34) т.е. будет
т.е. будет или
или 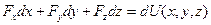 (35)
(35) (36)
(36) ,
,  – значение силовой функции в точках
– значение силовой функции в точках  . Следовательно, работа поступательной силы равна разности значений силовой функции в конечной и начальных точках пути, и от вида траектории движущейся точки не зависит.
. Следовательно, работа поступательной силы равна разности значений силовой функции в конечной и начальных точках пути, и от вида траектории движущейся точки не зависит. , считая
, считая 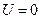 при
при 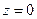 находим
находим 
 , считая
, считая 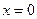 находим:
находим: 
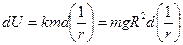 откуда считая
откуда считая 



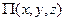 и
и 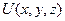 – совпадающими. Тогда
– совпадающими. Тогда  и по формуле (36)
и по формуле (36) 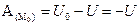
 ,
,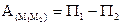 (37)
(37)

 - терема об изменении кинетической энергии)
- терема об изменении кинетической энергии)
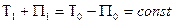 (38)
(38) ┴
┴  )
)
 ) …………………………………………………………
) …………………………………………………………



