
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Кинетическая и потенциальная энергии материальной точки.Содержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
Теорема об изменении кинетической энергии. Рассмотрим движение точки под действием силы Соотношение Проинтегрируем данное уравнение:
Эта формула выражает математическую запись теоремы об изменении кинетической энергии материальной точки: изменение кинетической энергии материальной точки равно работе силы, действующей на материальную точку. Если материальная точка движется в потенциальном поле, то работа сил может быть найдена по формуле:
Величина
Следовательно ЗАКОН СОХРАНЕНИЯ ПОЛНОЙ МЕХАНИЧЕСКОЙ ЭНЕРГИИ Запишем теорему об изменении кинетической энергии материальной точки:
Если сила, действующая на материальную точку, является консервативной:
Следовательно:
Сумму кинетической и потенциальной энергий материальной точки называют полной механической энергией материальной точки. Следовательно: полная механическая энергия материальной точки сохраняется, если на материальную точку действует консервативная сила. В случае действия на материальную точку нескольких сил
Если все силы консервативны:
Следовательно, в этом случае также выполняется закон сохранения полной механической энергии материальной точки. Пусть на материальную точку действуют n сил, но только m из них являются консервативными. При этом получим: Изменение полной механической энергии точки равно сумме работ неконсервативных сил, действующих на материальную точку. В результате вычисления в выражение для работы силы трения явно входит длина пути материальной точки. Эта значит, что сила трения не консервативна. При работе силы трения полная механическая энергия не сохраняется, переходя частично в тепло. Говорят, что в этом случае механическая энергия рассеивается или диссипирует. Поэтому силы трения и другие силы, при работе которых наблюдается переход механической энергии в другие виды энергий, называют диссипативными силами.
ДИНАМИКА МЕХАНИЧЕСКОЙ СИСТЕМЫ Динамической (механической) системой называют совокупность материальных тел, между которыми имеет место силовое взаимодействие. Совокупность материальных точек, между которыми происходит силовое взаимодействие, называют системой материальных точек. Любое материальное тело динамической системы можно мысленно разбить на большое число элементов и заменить эти элементы материальными точками, после этого механическая система рассматривается как совокупность материальных точек. Описать движение механической системы означает описать движение каждой материальной точки этой системы. Теорема об изменении импульса системы.
|
||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 682; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.140.188.174 (0.007 с.) |

 . Динамическое уравнение движения материальной точки запишем в виде:
. Динамическое уравнение движения материальной точки запишем в виде:  . Умножим это уравнение скалярно на величину
. Умножим это уравнение скалярно на величину 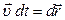 :
: 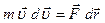 . Это можно записать так:
. Это можно записать так: 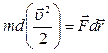 . Поскольку
. Поскольку  , то:
, то: 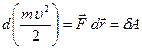 . Выражение, стоящее под знаком дифференциала, называют кинетической энергией точки:
. Выражение, стоящее под знаком дифференциала, называют кинетической энергией точки: 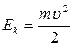 .
.
 . Введя величину
. Введя величину 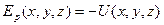 получим:
получим: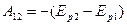
 имеет размерность энергии. Ее называют потенциальной энергией материальной точки. Потенциальная энергия материальной точки определяется не однозначно, а с точностью до произвольной постоянной. Это не может отразиться на физических выводах, так как ход физических явлений может зависеть не от значений самой потенциальной энергией, а лишь от ее разности в различных состояний. Эти же разности от выбора произвольной постоянной не зависят. Для примера рассмотрим силу тяжести:
имеет размерность энергии. Ее называют потенциальной энергией материальной точки. Потенциальная энергия материальной точки определяется не однозначно, а с точностью до произвольной постоянной. Это не может отразиться на физических выводах, так как ход физических явлений может зависеть не от значений самой потенциальной энергией, а лишь от ее разности в различных состояний. Эти же разности от выбора произвольной постоянной не зависят. Для примера рассмотрим силу тяжести: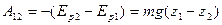
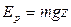 . Неоднозначность в определении потенциальной энергии материальной точки в поле силы тяжести связано с тем что, значение
. Неоднозначность в определении потенциальной энергии материальной точки в поле силы тяжести связано с тем что, значение  зависит от z, а следовательно и от выбора нулевого уровня, то есть плоскости, где z = 0. Кроме этого ясно, что
зависит от z, а следовательно и от выбора нулевого уровня, то есть плоскости, где z = 0. Кроме этого ясно, что 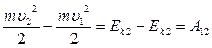

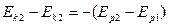 или
или 
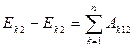
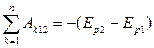
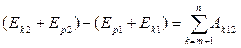 .
.


