
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Общие теоремы динамики материальной точки
И законы сохранения Общие теоремы динамики материальной точки есть логическое следствие основного закона динамики материальных тел: ТЕОРЕМА ОБ ИЗМЕНЕНИИ И ЗАКОН СОХРАНЕНИЯ ИМПУЛЬСА МАТЕРИАЛЬНОЙ ТОЧКИ Перепишем основной закон динамики материальной точки, используя определение ускорения: Интегрируя данное уравнение по промежутку времени ∆t = t2 – t1, получим интегральную формулировку теоремы об изменения импульса материальной точки:
В проекциях на оси координат:
Из уравнения Если ТЕОРЕМА ОБ ИЗМЕНЕНИИ И ЗАКОН СОХРАНЕНИЯ МОМЕНТА ИМПУЛЬСА МАТЕРИАЛЬНОЙ ТОЧКИ Моментом силы относительно произвольной точки О называют вектор
Модуль момента силы:
Момент силы направлен перпендикулярно плоскости, в которой находятся вектора  и и  . .
Здесь плечо силы – длина перпендикуляра, опущенного из начала вектора Совместив начало вектора
Аналогично моменту силы введём понятие момента импульса материальной точки:
Умножим левую и правую часть уравнения, выражающее теорему об изменении импульса материальной точки
Следовательно:
Если действует несколько сил, то:
В проекциях на оси декартовой системы координат:
Из теоремы об изменении момента импульса материальной точки следует: если момент сил, действующих на материальную точку равен нулю Работа силы. Мощность
Элементарной работой силы
В обозначении элементарной работы использована буква δ, а не d, чтобы отметить, что в общем случае линейная функция дифференциалов координат не является полным дифференциалом какой-либо функции координат. Определение элементарной работы показывает, что работа может быть: положительной, отрицательной, равной нулю в зависимости от угла
При этом мы использовали соотношение В декартовой системе координат:
Перейдём к определению работы на конечном перемещении. Пусть точка под действием приложенной к ней силы перемещается за некоторый промежуток времени из положения 1 в положение 2. Разобьем участок траектории 1-2 на n элементов, каждому из которых будет соответствовать свой вектор перемещения Тогда работа силы при перемещении материальной точки
Знак
Точное выражение для работы на конечном участке можно получить, если перейти к пределу при условии, что
Если сила постоянная
Размерность работы:
Единица измерения работы:
Скалярную величину, которая определяет работу силы в единицу времени называют мощностью:
Размерность мощности:
Единица измерения мощности в СИ ватт:
а) РАБОТА СИЛЫ ТЯЖЕСТИ: Пусть материальная точка движется под действием силы тяжести Вычислим работу силы тяжести при перемещении материальной точки из положения 1 в положение 2:
Отсюда видно, что работа силы тяжести может быть положительной, отрицательной, равной нулю. Работа силы тяжести не зависит от формы траектории, а определяется только начальным и конечным положением материальной точки. б) РАБОТА СИЛЫ УПРУГОСТИ: Вычислим работу силы упругости, которая подчиняется закону Гука:
Это соотношение показывает, что при увеличении деформации (r2>r1) работа силы упругости отрицательна, а при уменьшении деформации (r2<r1) – положительна. В одномерном случае:
В данном примере, как и в случае силы тяжести, работа зависит только от начального и конечного положения материальной точки и не зависит от пройденного этим телом пути под действием этих сил. в) РАБОТА СИЛЫ ТРЕНИЯ Сила трения характерна тем, что её вектор всегда направлен в сторону противоположную движению:
Вычислим работу силы трения:
Если модуль силы трения постоянен, то:
В данной формуле РАБОТА КОНСЕРВАТИВНЫХ СИЛ Силовое воздействие одних материальных тел на другие может осуществляться при непосредственном контакте (силы трения) или на расстоянии (гравитационные, электромагнитные силы). Воздействие на расстоянии осуществляется посредством особой формы материи, называемой физическим полем. Физическими полями называют также силовыми. О силовом поле говорят, если каждой точке пространства можно поставить в соответствие силу, действующую на материальную точку. В механике Ньютона предполагается, что силовое воздействие передаётся от одного тела к другому мгновенно. В любой точке пространства занятого силовым полем на материальную точку действует некоторая сила. Если сила, действующая на материальную точку, зависит только от положения этой точки в пространстве и не зависит от времени, то такое поле называют стационарным. Примером стационарных полей могут служить гравитационное поле Земли или поле неподвижного электрического заряда. Среди стационарных полей особый интерес представляют такие поля, для которых элементарная работа сил поля может быть найдена как бесконечно малое изменение (дифференциал) некоторой скалярной функции координат U (x, y, z). Такие поля называют потенциальными полями.
Полный дифференциал функции имеет вид
Сопоставляя записанные выражения, получаем:
Функцию U (x, y, z) называют силовой или потенциальной функцией. Ясно, что силовая функция U (x, y, z) определяется с точностью до константы. Вектор, компоненты которого представляют собой частные производные некоторые скалярной функции по координатам, называют градиентом этой функции:
Так как в потенциальном поле элементарная работа есть полный дифференциал от силовой функции
Это означает, что работа сил потенциального поля не зависит от траектории точки и от закона ее движения, а зависит только от значения силовой функции в начальном и конечном положении материальной точки и равна разности этих значений. Если точка будет перемещаться по замкнутому пути, то работа сил потенциального поля будет равна нулю, так как координаты начального и конечного положений точки при этом совпадают:
Поэтому равенство нулю работы на замкнутом пути служит признаком потенциального поля. В частности, если сила постоянна, то она обязательно потенциальна:
Силы, образующие потенциальное поле, называют консервативными силами. Результат, полученный при вычислении работы силы тяжести, показывает, что работа этой силы не зависит от пути, а определяется только начальными и конечными координатами материальной точки. Это означает, что поле силы тяжести является потенциальной, а сила тяжести является консервативной силой. В результат вычисления работы силы трения явно входит длина пути материальной почки. Это значит, что сила не является консервативной.
|
||||||||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 1221; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.216.124.8 (0.034 с.) |
 . Общие теоремы позволяют ввести ряд новых физических понятий, что позволяет полнее раскрыть закономерности механического движения.
. Общие теоремы позволяют ввести ряд новых физических понятий, что позволяет полнее раскрыть закономерности механического движения. . Т.к. m = const, то:
. Т.к. m = const, то:  . Вектор
. Вектор  – называют импульсом материальной точки или количеством движения материальной точки.
– называют импульсом материальной точки или количеством движения материальной точки.  – дифференциальная форма теоремы об изменении импульса материальной точки: дифференциал импульса материальной точки равен элементарному импульсу силы, приложенной к ней.
– дифференциальная форма теоремы об изменении импульса материальной точки: дифференциал импульса материальной точки равен элементарному импульсу силы, приложенной к ней.

 следует, что если
следует, что если  , то
, то  . В случае, когда на материальную точку действует несколько сил:
. В случае, когда на материальную точку действует несколько сил: 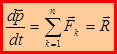 .
.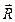 =0, то
=0, то  . Закон сохранения импульса материальной точки: если равнодействующая сил, приложенных к материальной точке равна нулю, то импульс материальной точки остаётся постоянным.
. Закон сохранения импульса материальной точки: если равнодействующая сил, приложенных к материальной точке равна нулю, то импульс материальной точки остаётся постоянным.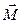 , определяемый формулой
, определяемый формулой , где
, где 

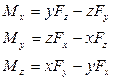


 , слева векторно на радиус-вектор точки:
, слева векторно на радиус-вектор точки:

 – теорема об изменении момента импульса материальной точки в дифференциальной форме: производная по времени от момента импульса материальной точки равна моменту силы, действующей на материальную точку.
– теорема об изменении момента импульса материальной точки в дифференциальной форме: производная по времени от момента импульса материальной точки равна моменту силы, действующей на материальную точку.
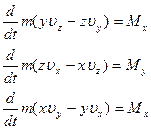
 , то момент импульса материальной точки сохраняется
, то момент импульса материальной точки сохраняется  – закон сохранения момента импульса материальной точки.
– закон сохранения момента импульса материальной точки.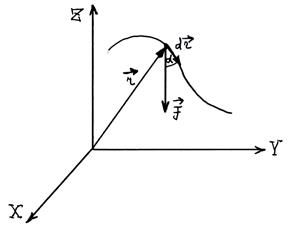 Пусть некоторая сила
Пусть некоторая сила  действует на материальную точку, которая перемещается под действием этой силы.
действует на материальную точку, которая перемещается под действием этой силы. материальной точки:
материальной точки:
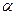 .
.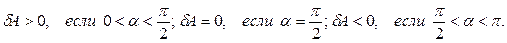
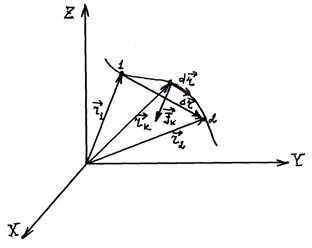 Выражение для элементарной работы можно записать и в другом виде, используя, что,
Выражение для элементарной работы можно записать и в другом виде, используя, что,  :
: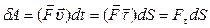
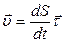 .
.
 . Когда материальная точка занимает k -тое положение на нее действует сила
. Когда материальная точка занимает k -тое положение на нее действует сила  .
.
 означает, что сила, действующая на материальную точку при перемещении на
означает, что сила, действующая на материальную точку при перемещении на  .
.
 , то величину
, то величину 
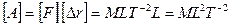

 .
.

 ПРИМЕРЫ ВЫЧИСЛЕНИЯ РАБОТЫ
ПРИМЕРЫ ВЫЧИСЛЕНИЯ РАБОТЫ .
.

 (положение материальной точки при отсутствии силы упругости совпадает с началом системы координат).
(положение материальной точки при отсутствии силы упругости совпадает с началом системы координат).


 , т.к.
, т.к.  >0, то
>0, то 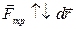 .
. , всегда <0.
, всегда <0.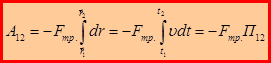
 – путь, пройденный материальной точкой за время от t 1 до t 2. Таким образом, работа силы трения зависит от пройденного материальной точкой пути.
– путь, пройденный материальной точкой за время от t 1 до t 2. Таким образом, работа силы трения зависит от пройденного материальной точкой пути. .
. .
.
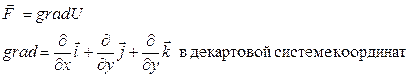
 , то работа при перемещении материальной точки из положения 1 в положение 2 будет равна:
, то работа при перемещении материальной точки из положения 1 в положение 2 будет равна:  .
.
 , если
, если 


