
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Закон сохранения полной механической энергии системы.Содержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
Запишем основной закон динамики для каждой точки:
Здесь Проинтегрируем записанное уравнение по времени: Просуммируем полученные уравнения: Здесь
Эта теорема справедлива для материального тела и для системы материальных тел. Под кинетической энергией материального тела понимаем: Под кинетической энергией системы материальных тел понимаем: Величина
Если только часть сил, действующих на элементы системы консервативны, то полная механическая энергия не сохраняется. Она может убывать или возрастать. ДИНАМИКА АБСОЛЮТНО ТВЁРДОГО ТЕЛА. Произвольное движение твердого тела можно описать с помощью двух теорем – теоремы об изменении момента импульса относительного центра масс и теоремы о движении центра масс. Рассмотрим простейшие случаи движения – поступательное и вращательное движение вокруг неподвижной оси. Динамика поступательного движения твердого тела.
Динамика вращения твердого тела вокруг неподвижной оси. КИНЕТИЧЕСКАЯ ЭНЕРГИЯ ВРАЩАЮЩЕГОСЯ ТВЁРДОГО ТЕЛА Вначале найдём выражение для кинетической энергии материальной точки, вращающейся с угловой скоростью
Кинетическая энергия твердого тела:
КИНЕТИЧЕСКАЯ ЭНЕРГИЯ ТВЁРДОГО ТЕЛА ПРИ СЛОЖНОМ ДВИЖЕНИИ
Найдём кинетическую энергию этого элемента в системе координат XYZ
Для нахождения кинетической энергии твёрдого тела необходимо сложить кинетические энергии бесконечно малых объёмов:
Кинетическая энергия твёрдого тела при произвольном движении равна сумме кинетической энергии поступательного движения со скоростью центра масс и кинетической энергии вращения вокруг мгновенной оси, проходящей вокруг центра масс. МОМЕНТЫ ИНЕРЦИИ ТВЁРДЫХ ТЕЛ
1) Момент инерции тонкостенного однородного цилиндра массы m и радиусом R относительно его оси симметрии:
получаем
С учётом
4) Момент инерции однородного шара массы m радиусом R относительно оси, проходящей через его середину. Приведём конечный результат без вывода:
В случае, когда момент инерции необходимо найти относительно произвольной оси задача существенно упрощается, если для её решения воспользоваться теоремой Штейнера. Момент инерции тела относительно произвольной оси равен сумме момента инерции относительно оси, параллельной данной и проходящей через центр масс тела и произведения массы тела m на квадрат расстояния между осями.
Пример: в соответствии с теоремой Штейнера найдем момент инерции
|
||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 427; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.139.69.138 (0.006 с.) |

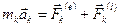 , k = 1, 2, 3,…, n. Умножим скалярно это уравнение на
, k = 1, 2, 3,…, n. Умножим скалярно это уравнение на  (учтено
(учтено  ):
): ,
,  .
. – элементарная работа внешних сил по перемещению k -ой материальной точки,
– элементарная работа внешних сил по перемещению k -ой материальной точки,  – элементарная работа внутренних сил по перемещению k -ой материальной точки.
– элементарная работа внутренних сил по перемещению k -ой материальной точки. .
.
 – кинетическая энергия системы материальных точек:
– кинетическая энергия системы материальных точек: – теорема об изменении кинетической энергии системы материальных точек: изменение кинетической энергии системы материальных точек равно сумме работ всех внешних и внутренних сил, действующих на элементы системы.
– теорема об изменении кинетической энергии системы материальных точек: изменение кинетической энергии системы материальных точек равно сумме работ всех внешних и внутренних сил, действующих на элементы системы. .
. . В случае, когда все внутренние силы системы являются консервативными:
. В случае, когда все внутренние силы системы являются консервативными:  . Тогда:
. Тогда:  . Если также и внешние силы консервативны:
. Если также и внешние силы консервативны:  , то:
, то: 
 – полная механическая энергия системы.
– полная механическая энергия системы. – закон сохранения полной механической энергии системы: если все внутренние и внешние силы, действующие на элементы системы консервативны, то ее полная механическая энергия сохраняется.
– закон сохранения полной механической энергии системы: если все внутренние и внешние силы, действующие на элементы системы консервативны, то ее полная механическая энергия сохраняется.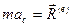 ,
,  , где
, где  – момент импульса твердого тела относительно центра масс;
– момент импульса твердого тела относительно центра масс;  - главный момент внешних сил относительно центра масс; m - масса твердого тела;
- главный момент внешних сил относительно центра масс; m - масса твердого тела; 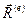 - главный вектор внешних сил.
- главный вектор внешних сил. При поступательном движении все точки твёрдого тела движутся одинаково, поэтому достаточно узнать, как будет двигаться центр масс тела:
При поступательном движении все точки твёрдого тела движутся одинаково, поэтому достаточно узнать, как будет двигаться центр масс тела: 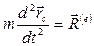
 Не следует думать, что теорема о кинетическом моменте не играет в этом случае никакой роли:
Не следует думать, что теорема о кинетическом моменте не играет в этом случае никакой роли: 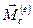 =0 (т.к.
=0 (т.к.  вокруг неподвижной оси OZ.
вокруг неподвижной оси OZ.  , где m – масса материальной точки. Но
, где m – масса материальной точки. Но  , следовательно:
, следовательно: 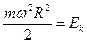
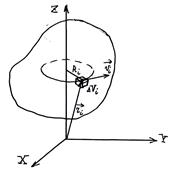 Величину
Величину  называют моментом инерции материальной точки относительно данной оси. Если выбрана ось OZ:
называют моментом инерции материальной точки относительно данной оси. Если выбрана ось OZ:  . Таким образом:
. Таким образом:  или
или  .
.  Рассмотрим твёрдое тело, вращающееся вокруг неподвижной оси. Кинетическая энергия i -го малого объема ∆V i твёрдого тела:
Рассмотрим твёрдое тело, вращающееся вокруг неподвижной оси. Кинетическая энергия i -го малого объема ∆V i твёрдого тела: 
 ;
; 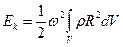 . Или:
. Или: 
 – момент инерции твёрдого тела относительно оси OZ.
– момент инерции твёрдого тела относительно оси OZ. Будем рассматривать сложное движение твердого тела как совокупность двух движений: поступательного со скоростью центра масс тела и вращения вокруг центра масс. Рассмотрим i -ый малый объем ∆Vi твёрдого тела:
Будем рассматривать сложное движение твердого тела как совокупность двух движений: поступательного со скоростью центра масс тела и вращения вокруг центра масс. Рассмотрим i -ый малый объем ∆Vi твёрдого тела: ;
;  ;
;
 ,
, 
 – скорость центра масс тела в системе, связанной с центром масс равна 0.
– скорость центра масс тела в системе, связанной с центром масс равна 0. ,
, 
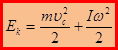 или
или 
 Момент инерции твёрдого
Момент инерции твёрдого  тела есть характеристика самого тела вне зависимости от его вращения. Величины
тела есть характеристика самого тела вне зависимости от его вращения. Величины  и R есть функции координат; интегрирование осуществляется по всему объёму. В общем случае неоднородного (
и R есть функции координат; интегрирование осуществляется по всему объёму. В общем случае неоднородного ( . С учетом
. С учетом  ,
,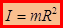
 2) Момент инерции сплошного однородного цилиндра массы m радиусом R и высотой H относительно его оси симметрии:
2) Момент инерции сплошного однородного цилиндра массы m радиусом R и высотой H относительно его оси симметрии:  . Разобьем цилиндр на бесконечно тонкие слои:
. Разобьем цилиндр на бесконечно тонкие слои: .
. , получаем:
, получаем: 
 3) Момент инерции тонкого однородного стержня массы m длиной ℓ относительно оси проходящей через его конец перпендикулярно его оси:
3) Момент инерции тонкого однородного стержня массы m длиной ℓ относительно оси проходящей через его конец перпендикулярно его оси:  .
. С учётом
С учётом  , получаем
, получаем 

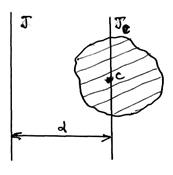 Теорема Штейнера
Теорема Штейнера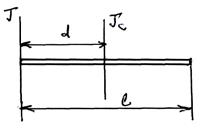

 тонкого однородного стержня относительно оси, проходящей через центр масс, если известен момент инерции
тонкого однородного стержня относительно оси, проходящей через центр масс, если известен момент инерции 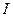 относительно оси, проходящей через конец стержня. Учтём, что
относительно оси, проходящей через конец стержня. Учтём, что  :
:  . Получим:
. Получим:  .
.


