
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Характер взаимодействия порции энергии — кванта – с веществом, оказался очень похожимСодержание книги
Поиск на нашем сайте 58. термоядерные реакции между лёгкими ат. ядрами, протекающие при очень высоких темп-рах (=108К и выше). Высокие темп-ры, т. е. достаточно большие относительные энергии сталкивающихся ядер, необходимы для преодоления электростатич. барьера, обусловленного взаимным отталкиванием ядер (как одноимённо заряж. ч-ц). Без этого невозможно сближение ядер на расстояние порядка радиуса действия яд. сил, а следовательно, и «перестройка» ядер, происходящая при Т. р. Поэтому Т. р. в природных условиях протекают лишь в недрах звёзд, а для их осуществления на Земле необходимо сильно разогреть в-во либо ядерным взрывом, либо мощным газовым разрядом, либо гигантским импульсом лазерного излучения или бомбардировкой интенсивным пучком ч-ц.
57. Цепная Ядерная Реакция Цепная ядерная реакция - самоподдерживающаяся реакция деления тяжелых ядер, в которой непрерывно воспроизводятся нейтроны, делящие все новые и новые ядра.
Ядро урана-235 под действием нейтрона делится на два радиоактивных осколка неравной массы, разлетающихся с большими скоростями в разные стороны, и два-три нейтрона. Например:
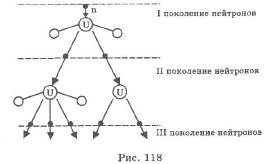
Нейтроны, вылетающие из ядра, могут вызвать реакцию деления соседних ядер 23592U, которые испускают нейтроны, способные вызвать дальнейшее деление. В результате число делящихся ядер урана быстро растет, возникает цепная реакция (рис. 118). Скорость нарастания цепной ядерной реакции характеризуют величиной, называемой коэффициентом размножения нейтронов. Коэффициент к размножения нейтронов характеризует быстроту роста числа нейтронов и равен отношению числа нейтронов в одном каком-либо поколении цепной реакции к породившему их числу нейтронов предшествующего поколения.
где Ni - число нейтронов в i-поколении, Ni-1- число нейтронов в предыдущем поколении. Необходимое условие протекания цепной ядерной реакции может быть выражено следующим образом: к >= 1.
При к = 1 число нейтронов, участвующих в делении ядер, остается неизменным, реакция протекает стационарно, имеет управляемый характер. При к > 1 число нейтронов увеличивается, интенсивность реакции возрастает и при к > 1,006 может принять неуправляемый характер; при к = 1,01 происходит взрыв. Ядерный реактор - устройство, в котором осуществляется управляемая цепная ядерная реакция (рис. 119). Главной частью ядерного реактора является активная зона 2 с блоками ядерного топлива 1. Управление протеканием ядерной реакции осуществляется с помощью регулирующих стержней 5 (кадмий, карбид бора и др.). Для увеличения коэффициента размножения нейтронов активную зону окружают отражатели нейтронов 3. Так как ядерный реактор является мощным источником нейтронов и у-излучения, в нем предусмотрена радиационная защита 4. Для отвода тепла применяется вода, жидкий натрий и др.; трубки с теплоносителем 7. Для замедления нейтронов в ядерных реакторах используется специальный замедлитель 6 (тяжелая вода или графит). Наименьшая масса делящегося вещества, при котором может протекать цепная реакция, называется критической массой. При этом к = 1: число нейтронов, потерянных вследствие захвата ядрами без деления и утечки, равно числу нейтронов, полученных в процессе деления. Для чистого (без замедлителя) 23592U, имеющего форму шара, критическая масса равна 50 кг, а радиус шара - примерно 9 см. Применяя замедлитель нейтронов и отражающую нейтроны оболочку из бериллия, удалось снизить критическую массу до 250 г. ЭНЕРГИЯ СВЯЗИ АТОМНЫХ ЯДЕР Важнейшую роль во всей ядерной физике играет понятие энергии связи ядра. Энергия связи позволяет объяснить устойчивость ядер, выяснить, какие процессы ведут к выделению ядерной энергии. Нуклоны в ядре прочно удерживаются ядерными силами. Для того чтобы удалить нуклон из ядра, надо совершить довольно большую работу, т. е. сообщить ядру значительную энергию. Под энергией связи ядра понимают ту энергию, которая необходима для полного расщепления ядра на отдельные нуклоны. На основе закона сохранения энергии можно также утверждать, что энергия связи ядра равна той энергии, которая выделяется при образовании ядра из отдельных частии. Энергия связи атомных ядер очень велика. Но как ее определить? В настоящее время рассчитать энергию связи теоретически, подобно тому как это можно сделать для электронов в атоме, не удается. Выполнить соответствующие расчеты можно, лишь применяя соотношение Эйнштейна между массой и энергией: Е = mс2. (13.3) Точнейшие измерения масс ядер показывают, что масса покоя ядра М21 всегда меньше суммы масс входящих в его состав протонов и нейтронов: Мя< Zmp + Nmn. (13.4) Существует, как говорят, дефект масс: разность масс
положительна. В частности, для гелия масса ядра на 0,75% меньше суммы масс двух протонов и двух нейтронов. Соответственно для гелия в количестве вещества один моль Уменьшение массы при образовании ядра из нуклонов означает, что при этом уменьшается энергия этой системы нуклонов на значение энергии связи Есв: Есв = Но куда при этом исчезают энергия Есв и масса При образовании ядра из частиц последние за счет действия ядерных сил на малых расстояниях устремляются с огромным ускорением друг к другу. Излучаемые при этом 55. Основные свойства и строение ядра. 1. Ядром называется центральная часть атома, в которой сосредоточена практически вся масса атома и его положительный электрический заряд. Все атомные ядра состоят из элементарных частиц: протонов и нейтронов, которые считаются двумя зарядовыми состояниями одной частицы - нуклона. Протон имеет положительный электрический заряд, равный по абсолютной величине заряду электрона. Нейтрон не имеет электрического заряда. 2. Зарядом ядра называется величина Ze, где е - величина заряда протона, Z - порядковый номер химического элемента в периодической системе Менделеева, равный числу протонов в ядре. В настоящее время известны ядра с Z от Z=1 до Z=107. Для всех ядер, кроме 3. Число нуклонов в ядре A=N+Z называется массовым числом. Нуклонам (протону и нейтрону) приписывается массовое число, равное единице, электрону - нулевое значение А.Ядра с одинаковыми Z, но различными А называются изотопами. Ядра, которые при одинаковом А имеют различные Z, называются изобарами. Ядро химического элемента X обозначается 4. Размер ядра характеризуется радиусом ядра, имеющим условный смысл ввиду размытости границы ядра. Эмпирическая формула для радиуса ядра 5. Ядерные частицы имеют собственные магнитные моменты, которыми определяется магнитный момент ядра Рmяд в целом. Единицей измерения магнитных моментов ядер служит ядерный магнетон mяд:
54. Планетарная модель атома Бора-Резерфорда. В 1911 году[3] Эрнест Резерфорд, проделав ряд экспериментов, пришёл к выводу, что атом представляет собой подобие планетной системы, в которой электроны движутся по орбитам вокруг расположенного в центре атома тяжёлого положительно заряженного ядра («модель атома Резерфорда»). Однако такое описание атома вошло в противоречие с классической электродинамикой. Дело в том, что, согласно классической электродинамике, электрон при движении с центростремительным ускорением должен излучать электромагнитные волны, а, следовательно, терять энергию. Расчёты показывали, что время, за которое электрон в таком атоме упадёт на ядро, совершенно ничтожно. Для объяснения стабильности атомов Нильсу Бору пришлось ввести постулаты, которые сводились к тому, что электрон в атоме, находясь в некоторых специальных энергетических состояниях, не излучает энергию («модель атома Бора-Резерфорда»). Постулаты Бора показали, что для описания атома классическая механика неприменима. Дальнейшее изучение излучения атома привело к созданию квантовой механики, которая позволила объяснить подавляющее большинство наблюдаемых фактов. 52. Спонтанное и индуцированное излучение Атомы и молекулы находятся в определенных энергетических состояниях, находятся на определенных энергетических уровнях. Для того, чтобы изолированный атом изменил свое энергетическое состояние, он должен либо поглотить фотон (получить энергию) и перейти на более высокий энергетический уровень, либо излучить фотон и перейти в более низкое энергетическое состояние. Если атом находится в возбужденном состоянии, то имеется определенная вероятность, что через некоторое время он перейдет в нижнее состояние и излучит фотон. Эта вероятность имеет две составляющие – постоянную и “переменную”. Если в области, где находится возбужденный атом отсутствует электромагнитное поле, то процесс перехода атома в нижнее состояние, сопровождаемый излучением фотона и характеризуемый постоянной составляющей вероятности перехода, называется спонтанным излучением. Спонтанное излучение не когерентно так как при этом различные атомы излучают независимо друг от друга. Если на атом действует внешнее электромагнитное поле с частотой, равной частоте излучаемого фотона, то процесс спонтанного перехода атома в нижнее энергетическое состояние продолжается по-прежнему, при этом фаза испускаемого атомом излучения не зависит от фазы внешнего поля. Однако, наличие внешнего электромагнитного поля с частотой, равной частоте излучаемого фотона, побуждает атомы испускать излучение, повышает вероятность перехода атома в нижнее энергетическое состояние. В этом случае излучение атома имеет ту же частоту, направление распространения и поляризацию, что и вынуждающее внешнее излучение. Излучение атомов будет находиться в отдельном фазовом состоянии с внешним полем, то есть будет когерентным. Такой процесс излучения называется индуцированным (или вынужденным) и характеризуется “переменной” составляющей вероятности (она тем больше, чем больше плотность энергии внешнего электромагнитного поля). Поскольку на стимулирование перехода энергия электромагнитного поляне расходуется, то энергия внешнего поля увеличивается на величину энергии испущенных фотонов. Эти процессы постоянно происходят вокруг нас, так как световые волны всегда взаимодействуют с веществом. Однако одновременно протекают и обратные процессы. Атомы поглощают фотоны и становятся возбужденными, а энергия электромагнитного поля уменьшается на величину энергии поглощенных фотонов. В природе существует равновесие между процессами испускания и поглощения, следовательно, в среднем в окружающей нас природе нет процесса усиления электромагнитного поля. Пусть имеем двухуровневую систему.
Схема переходов в двухуровневой системе N2 – число атомов в единице объема в возбужденном состоянии 2. N1 – в невозбужденном состоянии 1. dN2 = - A21 N2 dt, число атомов в единице объема, покинувших состояние 2. A21 – вероятностьспонтанного перехода отдельного атома из состояния 2 в состояние 1. Проинтегрировав, получим N2 = N20 eA21t, где N20 – число атомов в состоянии 2 в момент времени t = 0. Интенсивность спонтанного излучения Ic равна Ic = (hμ21 dN2) / dt = hμ21 A21 N2 = hμ21 A21 N20 e – A21t, Интенсивность спонтанного излучения убывает по экспонентциальному закону. Число атомов, покидающих состояние 2за время от t до t +dt, равно A21 N2dt, то есть это число атомов, которое прожило время t в состоянии 2. Отсюда среднее время жизни τ атома в состоянии 2 равно τ = (1 / N20) dt = (1 / A21)τ = 1 / A21 Ic = hμ21 A21 N20 e – A21t = (hμ21 N20 / τ) · e Вероятностью индунцированного перехода W21 2 – 1 пропорционально спектральной плотности энергии электромагнитного поля ρν на частоте перехода, то есть W21 = B21 ρν, B21 – коэффициент Эйнштейна индуцированного излучения. Вероятность перехода 1- 2 W12 = B12 ρν, ρν = (8πhμ321 / c3) · (1 / e -1) формула Планка. 51. Гипотеза де Бройля заключается в том, что французский физик Луи де Бройль выдвинул идею приписать волновые свойства электрону. Проводя аналогию между квантом, де Бройль предположил, что движение электрона или какой-либо другой частицы, обладающей массой покоя, связано с волновым процессом. Гипотеза де Бройля устанавливает, что движущейся частице, обладающей энергией E и импульсом p, соответствует волновой процесс, частота которого равна:
а длина волны:
где p - импульс движущейся частицы.
Утверждение о том, что произведение неопределенностей значений двух сопряженных переменных не может быть по порядку меньше постоянной Планка h, называется соотношением неопределенностей Гейзенберга. Энергия и время являются канонически сопряженными величинами. Поэтому для них также справедливо соотношение неопределенностей:
Это соотношение означает, что определение энергии с точностью должно занять интервал времени, равный, по меньшей мере,
Соотношение неопределенностей получено при одновременном использовании классических характеристик движения частицы (координаты, импульса) и наличии у нее волновых свойств. Т.к. в классической механике принимается, что измерение координаты и импульса может быть произведено с любой точностью, то соотношение неопределенностей является, таким образом, квантовым ограничением применимости классической механики к микрообъектам. 50. Закон Стефана — Больцмана и закон Вина
Теоретическое объяснение законов излучения абсолютно черного тела имело огромное значение в истории физики – оно привело к понятию квантов энергии. Долгое время попытки получить теоретически вид функции f(ω,Т) не давали общего решения задачи. Стефан (1879), анализируя экспериментальные данные, пришел к выводу, что энергетическая светимость R любого тела пропорциональна четвертой степени абсолютной температуры. Однако последующие более точные измерения показали ошибочность его выводов. Больцман (1884), исходя из термодинамических соображений, получил теоретически для энергетической светимости абсолютно черного тела следующее значение: (3.1) где σ – постоянная величина; Т—абсолютная температура. Таким образом, заключение, к которому Стефан пришел для нечерных тел (с абсолютно черными телами он не экспериментировал), оказалось справедливым лишь для абсолютно черных тел. Соотношение (3.1) между энергетической светимостью абсолютно черного тела и его абсолютной температурой получило название закона Стефана – Больцмана. Константу σ называют постоянной Стефана – Больцмана. Ее экспериментальное значение равно: (3.2) Вин (1893), воспользовавшись, кроме термодинамики, электромагнитной теорией, показал, что функция спектрального распределения должна иметь вид: где F – некоторая функция отношения частоты к температуре. Согласно формуле (2.10) для функции φ(λ,Т) получается выражение: где ψ(λ,Т) – некоторая функция произведения λТ. Соотношение (3.4) позволяет установить зависимость между длиной волны λm, на которую приходится максимум функции φ(λ,Т), и температурой. Продифференцируем это соотношение по λ: Выражение в квадратных скобках представляет собой некоторую функцию ψ(λ,Т). При длине волны λm, соответствующей максимуму функции φ(λ,Т), выражение (3.5) должно обращаться в нуль:
Из опыта известно, что λm конечно (λm ≠ 0). Поэтому должно выполняться условие: ψ(λ,Т)=0. Решение последнего уравнения относительно неизвестного λmТ дает для этого неизвестного некоторое число, которое мы обозначим буквой b. Таким образом, получается соотношение:
которое носит название закона смещения Вина. Экспериментальное значение константы b равно:
49. Распределение энергии в спектре абсолютно черного тела для Δλ = 1 мкм при температурах 200 и 300 К. 47. Фотоны. Энергия и импульс фотона 58. термоядерные реакции между лёгкими ат. ядрами, протекающие при очень высоких темп-рах (=108К и выше). Высокие темп-ры, т. е. достаточно большие относительные энергии сталкивающихся ядер, необходимы для преодоления электростатич. барьера, обусловленного взаимным отталкиванием ядер (как одноимённо заряж. ч-ц). Без этого невозможно сближение ядер на расстояние порядка радиуса действия яд. сил, а следовательно, и «перестройка» ядер, происходящая при Т. р. Поэтому Т. р. в природных условиях протекают лишь в недрах звёзд, а для их осуществления на Земле необходимо сильно разогреть в-во либо ядерным взрывом, либо мощным газовым разрядом, либо гигантским импульсом лазерного излучения или бомбардировкой интенсивным пучком ч-ц.
57. Цепная Ядерная Реакция Цепная ядерная реакция - самоподдерживающаяся реакция деления тяжелых ядер, в которой непрерывно воспроизводятся нейтроны, делящие все новые и новые ядра.
Ядро урана-235 под действием нейтрона делится на два радиоактивных осколка неравной массы, разлетающихся с большими скоростями в разные стороны, и два-три нейтрона. Например:
Нейтроны, вылетающие из ядра, могут вызвать реакцию деления соседних ядер 23592U, которые испускают нейтроны, способные вызвать дальнейшее деление. В результате число делящихся ядер урана быстро растет, возникает цепная реакция (рис. 118). Скорость нарастания цепной ядерной реакции характеризуют величиной, называемой коэффициентом размножения нейтронов. Коэффициент к размножения нейтронов характеризует быстроту роста числа нейтронов и равен отношению числа нейтронов в одном каком-либо поколении цепной реакции к породившему их числу нейтронов предшествующего поколения.
где Ni - число нейтронов в i-поколении, Ni-1- число нейтронов в предыдущем поколении. Необходимое условие протекания цепной ядерной реакции может быть выражено следующим образом: к >= 1.
При к = 1 число нейтронов, участвующих в делении ядер, остается неизменным, реакция протекает стационарно, имеет управляемый характер. При к > 1 число нейтронов увеличивается, интенсивность реакции возрастает и при к > 1,006 может принять неуправляемый характер; при к = 1,01 происходит взрыв. Ядерный реактор - устройство, в котором осуществляется управляемая цепная ядерная реакция (рис. 119). Главной частью ядерного реактора является активная зона 2 с блоками ядерного топлива 1. Управление протеканием ядерной реакции осуществляется с помощью регулирующих стержней 5 (кадмий, карбид бора и др.). Для увеличения коэффициента размножения нейтронов активную зону окружают отражатели нейтронов 3. Так как ядерный реактор является мощным источником нейтронов и у-излучения, в нем предусмотрена радиационная защита 4. Для отвода тепла применяется вода, жидкий натрий и др.; трубки с теплоносителем 7. Для замедления нейтронов в ядерных реакторах используется специальный замедлитель 6 (тяжелая вода или графит). Наименьшая масса делящегося вещества, при котором может протекать цепная реакция, называется критической массой. При этом к = 1: число нейтронов, потерянных вследствие захвата ядрами без деления и утечки, равно числу нейтронов, полученных в процессе деления. Для чистого (без замедлителя) 23592U, имеющего форму шара, критическая масса равна 50 кг, а радиус шара - примерно 9 см. Применяя замедлитель нейтронов и отражающую нейтроны оболочку из бериллия, удалось снизить критическую массу до 250 г. ЭНЕРГИЯ СВЯЗИ АТОМНЫХ ЯДЕР Важнейшую роль во всей ядерной физике играет понятие энергии связи ядра. Энергия связи позволяет объяснить устойчивость ядер, выяснить, какие процессы ведут к выделению ядерной энергии. Нуклоны в ядре прочно удерживаются ядерными силами. Для того чтобы удалить нуклон из ядра, надо совершить довольно большую работу, т. е. сообщить ядру значительную энергию. Под энергией связи ядра понимают ту энергию, которая необходима для полного расщепления ядра на отдельные нуклоны. На основе закона сохранения энергии можно также утверждать, что энергия связи ядра равна той энергии, которая выделяется при образовании ядра из отдельных частии. Энергия связи атомных ядер очень велика. Но как ее определить? В настоящее время рассчитать энергию связи теоретически, подобно тому как это можно сделать для электронов в атоме, не удается. Выполнить соответствующие расчеты можно, лишь применяя соотношение Эйнштейна между массой и энергией: Е = mс2. (13.3) Точнейшие измерения масс ядер показывают, что масса покоя ядра М21 всегда меньше суммы масс входящих в его состав протонов и нейтронов: Мя< Zmp + Nmn. (13.4) Существует, как говорят, дефект масс: разность масс
положительна. В частности, для гелия масса ядра на 0,75% меньше суммы масс двух протонов и двух нейтронов. Соответственно для гелия в количестве вещества один моль Уменьшение массы при образовании ядра из нуклонов означает, что при этом уменьшается энергия этой системы нуклонов на значение энергии связи Есв: Есв = Но куда при этом исчезают энергия Есв и масса При образовании ядра из частиц последние за счет действия ядерных сил на малых расстояниях устремляются с огромным ускорением друг к другу. Излучаемые при этом 55. Основные свойства и строение ядра. 1. Ядром называется центральная часть атома, в которой сосредоточена практически вся масса атома и его положительный электрический заряд. Все атомные ядра состоят из элементарных частиц: протонов и нейтронов, которые считаются двумя зарядовыми состояниями одной частицы - нуклона. Протон имеет положительный электрический заряд, равный по абсолютной величине заряду электрона. Нейтрон не имеет электрического заряда. 2. Зарядом ядра называется величина Ze, где е - величина заряда протона, Z - порядковый номер химического элемента в периодической системе Менделеева, равный числу протонов в ядре. В настоящее время известны ядра с Z от Z=1 до Z=107. Для всех ядер, кроме 3. Число нуклонов в ядре A=N+Z называется массовым числом. Нуклонам (протону и нейтрону) приписывается массовое число, равное единице, электрону - нулевое значение А.Ядра с одинаковыми Z, но различными А называются изотопами. Ядра, которые при одинаковом А имеют различные Z, называются изобарами. Ядро химического элемента X обозначается 4. Размер ядра характеризуется радиусом ядра, имеющим условный смысл ввиду размытости границы ядра. Эмпирическая формула для радиуса ядра 5. Ядерные частицы имеют собственные магнитные моменты, которыми определяется магнитный момент ядра Рmяд в целом. Единицей измерения магнитных моментов ядер служит ядерный магнетон mяд:
54. Планетарная модель атома Бора-Резерфорда. В 1911 году[3] Эрнест Резерфорд, проделав ряд экспериментов, пришёл к выводу, что атом представляет собой подобие планетной системы, в которой электроны движутся по орбитам вокруг расположенного в центре атома тяжёлого положительно заряженного ядра («модель атома Резерфорда»). Однако такое описание атома вошло в противоречие с классической электродинамикой. Дело в том, что, согласно классической электродинамике, электрон при движении с центростремительным ускорением должен излучать электромагнитные волны, а, следовательно, терять энергию. Расчёты показывали, что время, за которое электрон в таком атоме упадёт на ядро, совершенно ничтожно. Для объяснения стабильности атомов Нильсу Бору пришлось ввести постулаты, которые сводились к тому, что электрон в атоме, находясь в некоторых специальных энергетических состояниях, не излучает энергию («модель атома Бора-Резерфорда»). Постулаты Бора показали, что для описания атома классическая механика неприменима. Дальнейшее изучение излучения атома привело к созданию квантовой механики, которая позволила объяснить подавляющее большинство наблюдаемых фактов. 52. Спонтанное и индуцированное излучение Атомы и молекулы находятся в определенных энергетических состояниях, находятся на определенных энергетических уровнях. Для того, чтобы изолированный атом изменил свое энергетическое состояние, он должен либо поглотить фотон (получить энергию) и перейти на более высокий энергетический уровень, либо излучить фотон и перейти в более низкое энергетическое состояние. Если атом находится в возбужденном состоянии, то имеется определенная вероятность, что через некоторое время он перейдет в нижнее состояние и излучит фотон. Эта вероятность имеет две составляющие – постоянную и “переменную”. Если в области, где находится возбужденный атом отсутствует электромагнитное поле, то процесс перехода атома в нижнее состояние, сопровождаемый излучением фотона и характеризуемый постоянной составляющей вероятности перехода, называется спонтанным излучением. Спонтанное излучение не когерентно так как при этом различные атомы излучают независимо друг от друга. Если на атом действует внешнее электромагнитное поле с частотой, равной частоте излучаемого фотона, то процесс спонтанного перехода атома в нижнее энергетическое состояние продолжается по-прежнему, при этом фаза испускаемого атомом излучения не зависит от фазы внешнего поля. Однако, наличие внешнего электромагнитного поля с частотой, равной частоте излучаемого фотона, побуждает атомы испускать излучение, повышает вероятность перехода атома в нижнее энергетическое состояние. В этом случае излучение атома имеет ту же частоту, направление распространения и поляризацию, что и вынуждающее внешнее излучение. Излучение атомов будет находиться в отдельном фазовом состоянии с внешним полем, то есть будет когерентным. Такой процесс излучения называется индуцированным (или вынужденным) и характеризуется “переменной” составляющей вероятности (она тем больше, чем больше плотность энергии внешнего электромагнитного поля). Поскольку на стимулирование перехода энергия электромагнитного поляне расходуется, то энергия внешнего поля увеличивается на величину энергии испущенных фотонов. Эти процессы постоянно происходят вокруг нас, так как световые волны всегда взаимодействуют с веществом. Однако одновременно протекают и обратные процессы. Атомы поглощают фотоны и становятся возбужденными, а энергия электромагнитного поля уменьшается на величину энергии поглощенных фотонов. В природе существует равновесие между процессами испускания и поглощения, следовательно, в среднем в окружающей нас природе нет процесса усиления электромагнитного поля. Пусть имеем двухуровневую систему.
Схема переходов в двухуровневой системе N2 – число атомов в единице объема в возбужденном состоянии 2. N1 – в невозбужденном состоянии 1. dN2 = - A21 N2 dt, число атомов в единице объема, покинувших состояние 2. A21 – вероятностьспонтанного перехода отдельного атома из состояния 2 в состояние 1. Проинтегрировав, получим N2 = N20 eA21t, где N20 – число атомов в состоянии 2 в момент времени t = 0. Интенсивность спонтанного излучения Ic равна Ic = (hμ21 dN2) / dt = hμ21 A21 N2 = hμ21 A21 N20 e – A21t, Интенсивность спонтанного излучения убывает по экспонентциальному закону. Число атомов, покидающих состояние 2за время от t до t +dt, равно A21 N2dt, то есть это число атомов, которое прожило время t в состоянии 2. Отсюда среднее время жизни τ атома в состоянии 2 равно τ = (1 / N20) dt = (1 / A21)τ = 1 / A21 Ic = hμ21 A21 N20 e – A21t = (hμ21 N20 / τ) · e Вероятностью индунцированного перехода W21 2 – 1 пропорционально спектральной плотности энергии электромагнитного поля ρν на частоте перехода, то есть W21 = B21 ρν, B21 – коэффициент Эйнштейна индуцированного излучения. Вероятность перехода 1- 2 W12 = B12 ρν, ρν = (8πhμ321 / c3) · (1 / e -1) формула Планка. 51. Гипотеза де Бройля заключается в том, что французский физик Луи де Бройль выдвинул идею приписать волновые свойства электрону. Проводя аналогию между квантом, де Бройль предположил, что движение электрона или какой-либо другой частицы, обладающей массой покоя, связано с волновым процессом. Гипотеза де Бройля устанавливает, что движущейся частице, обладающей энергией E и импульсом p, соответствует волновой процесс, частота которого равна:
а длина волны:
где p - импульс движущейся частицы.
Утверждение о том, что произведение неопределенностей значений двух сопряженных переменных не может быть по порядку меньше постоянной Планка h, называется соотношением неопределенностей Гейзенберга. Энергия и время являются канонически сопряженными величинами. Поэтому для них также справедливо соотношение неопределенностей:
Это соотношение означает, что определение энергии с точностью должно занять интервал времени, равный, по меньшей мере,
Соотношение неопределенностей получено при одновременном использовании классических характеристик движения частицы (координаты, импульса) и наличии у нее волновых свойств. Т.к. в классической механике принимается, что измерение координаты и импульса может быть произведено с любой точностью, то соотношение неопределенностей является, таким образом, квантовым ограничением применимости классической механики к микрообъектам. 50. Закон Стефана — Больцмана и закон Вина
Теоретическое объяснение законов излучения абсолютно черного тела имело огромное значение в истории физики – оно привело к понятию квантов энергии. Долгое время попытки получить теоретически вид функции f(ω,Т) не давали общего решения задачи. Стефан (1879), анализируя экспериментальные данные, пришел к выводу, что энергетическая светимость R любого тела пропорциональна четвертой степени абсолютной температуры. Однако последующие более точные измерения показали ошибочность его выводов. Больцман (1884), исходя из термодинамических соображений, получил теоретически для энергетической светимости абсолютно черного тела следующее значение: (3.1) где σ – постоянная величина; Т—абсолютная температура. Таким образом, заключение, к которому Стефан пришел для нечерных тел (с абсолютно черными телами он не экспериментировал), оказалось справедливым лишь для абсолютно черных тел. Соотношение (3.1) между энергетической светимостью абсолютно черного тела и его абсолютной температурой получило название закона Стефана – Больцмана. Константу σ называют постоянной Стефана – Больцмана. Ее экспериментальное значение равно: (3.2) Вин (1893), воспользовавшись, кроме термодинамики, электром
|
||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 325; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.108 (0.013 с.) |


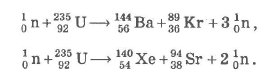
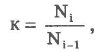
 М = Zmp + Nmn - Мя
М = Zmp + Nmn - Мя -кванты как раз обладают енергией Есв и массой
-кванты как раз обладают енергией Есв и массой  .
.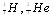 и некоторых других нейтронодефицитных ядер NіZ, где N - число нейтронов в ядре. Для легких ядер N/Z»1; для ядер химических элементов, расположенных в конце периодической системы, N/Z»1,6.
и некоторых других нейтронодефицитных ядер NіZ, где N - число нейтронов в ядре. Для легких ядер N/Z»1; для ядер химических элементов, расположенных в конце периодической системы, N/Z»1,6. , где Х - символ химического элемента.Всего известно около 300 устойчивых изотопов химических элементов и более 2000 естественных и искусственно полученных радиоактивных изотопов.
, где Х - символ химического элемента.Всего известно около 300 устойчивых изотопов химических элементов и более 2000 естественных и искусственно полученных радиоактивных изотопов.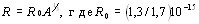 м, может быть истолкована как пропорциональность объема ядра числу нуклонов в нем.Плотность ядерного вещества составляет по порядку величины 1017 кг/м3 и постоянна для всех ядер. Она значительно превосходит плотности самых плотных обычных веществ.
м, может быть истолкована как пропорциональность объема ядра числу нуклонов в нем.Плотность ядерного вещества составляет по порядку величины 1017 кг/м3 и постоянна для всех ядер. Она значительно превосходит плотности самых плотных обычных веществ. (в СИ)
(в СИ) (в СГС).Здесь е - абсолютная величина заряда электрона, mp - масса протона, с - электродинамическая постоянная. Ядерный магнетон в
(в СГС).Здесь е - абсолютная величина заряда электрона, mp - масса протона, с - электродинамическая постоянная. Ядерный магнетон в  раз меньше магнетона Бора, откуда следует, что магнитные свойства атомов определяются магнитными свойствами его электронов.6. Распределение электрического заряда протонов по ядру в общем случае несимметрично. Мерой отклонения этого распределения от сферически симметричного является квадрупольный электрический момент ядра Q. Если плотность заряда считается везде одинаковой, то Q определяется только формой ядра.
раз меньше магнетона Бора, откуда следует, что магнитные свойства атомов определяются магнитными свойствами его электронов.6. Распределение электрического заряда протонов по ядру в общем случае несимметрично. Мерой отклонения этого распределения от сферически симметричного является квадрупольный электрический момент ядра Q. Если плотность заряда считается везде одинаковой, то Q определяется только формой ядра.
 21 N2 tdt = A21
21 N2 tdt = A21  e-A21t
e-A21t


 .
.










