
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вопрос1 Кинематическое описание движения материальной точкиСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Вопрос1 Кинематическое описание движения материальной точки материальная точка – тело, обладающее массой, размерами которого в данной задаче можно пренебречь.С истема отсчета это совокупность системы координат и часов, связанных с телом отсчета.
Траектория движения материальной точки – линия, описываемая этой точкой в пространстве.
Направление вектора средней скорости совпадает с направлением
Средним ускорением неравномерного движения в интервале от t до Мгновенным ускорением a (ускорением) материальной точки в момент времени t будет предел среднего ускорения:
Вопрос3 Кинематика вращательного движения
Угловым ускорением называется векторная величина, равная первой производной угловой скорости по времени: Тангенциальная составляющая ускорения Нормальная составляющая ускорения
Таким образом, связь между линейными (длина пути s, пройденного точкой по дуге окружности радиуса R, линейная скорость v, тангенциальное ускорение В случае равнопеременного движения точки по окружности (
Вопрос2 Криволинейное движение Тангенциальная составляющая ускорения т. е., определяет быстроту изменения скорости по модулю.
Вторая составляющая ускорения, равная называется нормальной составляющей ускорения и направлена по нормали к траектории к центру се кривизны (поэтому ее называют также центростремительным ускорением).
тангенциальная составляющая ускорения характеризует быстроту изменения скорости по модулю (направлена по касательной к траектории), а нормальная составляющая ускорения – быстроту изменения скорости по направлению (направлена к центру кривизны траектории).
В зависимости от тангенциальной и нормальной составляющих ускорения движение можно классифицировать следующим образом: 1) 2) 3) 4) 5) 6) 7)
Вопрос 6 Работа, мощность. Элементарной работой силы F на перемещении dr называется скалярная величина dA = F d r = F cos ds = Fsds,
Работа силы на участке траектории от точки 1 до точки 2 равна алгебраической сумме элементарных работ на отдельных бесконечно малых участках пути, а в пределе интегралу
Единица работы – джоуль (Дж): 1 Дж – работа, совершаемая силой 1 Н на пути 1 м (1 Дж=1 Нм). Чтобы охарактеризовать скорость совершения работы, вводят понятие мощности
За время dt сила F совершает работу F d r, и мощность, развиваемая этой силой, в данный момент времени т. е. равна скалярному произведению вектора силы на вектор скорости, с которой движется точка приложения этой силы; N – величина скалярная. Единица мощности – ватт (Вт): 1 Вт – мощность, при которой за время 1 с совершается работа 1 Дж (1 Вт=1 Дж/с).
Вопрос 7 Энергия Кинетическая энергия механической системы – это энергия ее механического движения этой системы.
Таким образом, тело массой т, движущееся со скоростью v, обладает кинетической энергией
Потенциальная энергия – это механическая энергия системы тел, определяемая их взаимным расположением и характером сил взаимодействия между ними. Если работа, совершаемая под действием силовых полей при перемещении тела из одного положения в другое, не зависит от того, по какой траектории это перемещение произошло, а зависит только от начального и конечного положений, то поля называются потенциальными, а силы, действующие в них, – консервативными. Если же работа, совершаемая силой, зависит от траектории перемещения тела из одной точки в другую, то такая сила называется диссипативной; например сила трения. Тело, находясь в потенциальном поле сил, обладает потенциальной энергией П. Работа консервативных сил при бесконечно малом изменении конфигурации системы равна приращению потенциальной энергии, взятому со знаком минус, так как работа совершается за счет убыли потенциальной энергии:
Затухающие колебания. Дифференциальное уравнение затухающих колебаний и его решение. Амплитуда и частота затухающих колебаний. Декремент, логарифмический декремент затухания, время релаксации, добротность. Затухающие колебания -колебания, энергия которых уменьшается с течением времени за счет действия сил сопротивления. 1. Механические: Пусть Fсопр=-hv (сила сопротивления пропорциональна скорости колебаний) = - hx¢, h -к-т сопротивления. Тогда по 2-му з-ну Ньютона: mx¢¢=- hx¢ - кх(=Fтр). Обозначим :b=h/2m -коэффициент затухания; w02=k/m- собственная частота свободных колебаний. x¢¢+2bх¢+w02х=0
При условии b>w0 - затух колебаний нет - апериодический возврат в положение равновесия При условии b<w0 - затухающие колебания
Логарифмический декремент и коэффициент затухания:
Если A(t), A(t+T), амплитуды двух последовательных колебаний то отношение
Физический и математический маятник.Физический маятник. Дифференциальное уравнение колебания и его решение. Период колебаний физического маятника. Приведенная длина. Математический маятник. Период колебания математического маятника. Математический маятник. Математическим маятником называется материальная точка, подвешенная на нерастяжимой невесомой нити, совершающая колебательное движение в одной вертикальной плоскости под действием силы тяжести.
Таким маятником можно считать тяжелый шар массой m, подвешенный на тонкой нити, длина l которой намного больше размеров шара. Если его отклонить на угол α (рис.7.3.) от вертикальной линии, то под влиянием силы F – одной из составляющих веса Р он будет совершать колебания. Другая составляющая
Знак минус в правой части означает то, что сила F направлена в сторону уменьшения угла α. С учетом малости угла α
Для вывода закона движения математического и физического маятников используем основное уравнение динамики вращательного движения
Момент силы относительно точки О: С учетом этих величин имеем: или
Его решение
Как видим, период колебаний математического маятника зависит от его длины и ускорения силы тяжести и не зависит от амплитуды колебаний. Физический маятник. Физическим маятником называется твердое тело, закрепленное на неподвижной горизонтальной ocи (оси подвеса), не проходящей через центр тяжести, и совершающее колебания относительно этой оси под действием силы тяжести. В отличие от математического маятника массу такого тела нельзя считать точечной.
При небольших углах отклонения α (рис. 7.4) физический маятник так же совершает гармонические колебания. Будем считать, что вес физического маятника приложен к его центру тяжести в точке С. Силой, которая возвращает маятник в положение равновесия, в данном случае будет составляющая силы тяжести – сила F.
Знак минус в правой части означает то, что сила F направлена в сторону уменьшения угла α. С учетом малости угла α
Для вывода закона движения математического и физического маятников используем основное уравнение динамики вращательного движения
Решение этого уравнения Определим длину l математического маятника, при которой период его колебаний равен периоду колебаний физического маятника, т.е.
Данная формула определяет приведенную длину физического маятника, т.е. длину такого математического маятника, период колебаний которого равен периоду колебаний данного физического маятника. Вопрос 16 Идеальный газ Для вывода основного уравнения молекулярно-кинетической теории рассмотрим идеальный одноатомный газ. Предположим, что молекулы газа движутся хаотически, число взаимных столкновений между молекулами газа пренебрежимо мало по сравнению с числом ударов о стенки сосуда, а соударения молекул со стенками сосуда абсолютно упругие. Выделим на стенке сосуда некоторую элементарную площадку S (рисунок 2.5) и вычислим давление, оказываемое на эту площадку. При каждом соударении молекула, движущаяся перпендикулярно площадке, передает ей импульс
где m0 – масса молекулы, v – ее скорость. За время t площадки S достигнут только те молекулы, которые заключены в объеме цилиндра с основанием S и высотой v t (рисунок 2.5). Число этих молекул равно n Sv t (n – концентрация молекул). Необходимо учитывать, что реально молекулы движутся к площадке S под разными углами и имеют различные скорости, причем скорость молекул при каждом соударении меняется. Для упрощения расчетов хаотическое движение молекул заменяют движением вдоль трех взаимно перпендикулярных направлений, так что в любой момент времени вдоль каждого из них движется 1/3 молекул. Половина этих молекул (т.е. 1/6 часть) движется вдоль данного направления в одну сторону, а вторая половина – в противоположную. Тогда число ударов молекул, движущихся в заданном направлении, о площадку S будет 1/6 n Sv t. При столкновении с площадкой эти молекулы передадут ей импульс P = 2m0v1/6nSvt = 1/3nm0v2St Тогда давление газа, оказываемое им на стенку сосуда,
Если газ в объеме V содержит N молекул, движущихся со скоростями v1, v2,..., vN, то целесообразно рассматривать среднюю квадратичную скорость
характеризующую всю совокупность молекул газа. Уравнение (2.23) с учетом (2.24) примет вид
Выражение (2.25) называется основным уравнением молекулярно-кинетической теории идеальных газов. Уравнению PVm = RT удовлетворяет лишь идеальный газ, и оно является уравнением состояния идеального газа, называемым также уравнением Клапейрона – Менделеева. В молекулярно-кинетической теории пользуются моделью идеального газа, согласно которой считают, что: 1) собственный объем молекул газа пренебрежимо мал по сравнению с объемом сосуда; 2) между молекулами газа отсутствуют силы взаимодействия; 3) столкновения молекул газа между собой и со стенками сосуда абсолютно упругие. Модель идеального газа можно использовать при изучении реальных газов в условиях, близких к нормальным (например, кислород и гелий), а также при низких давлениях и высоких температурах. Вопрос1 Кинематическое описание движения материальной точки материальная точка – тело, обладающее массой, размерами которого в данной задаче можно пренебречь.С истема отсчета это совокупность системы координат и часов, связанных с телом отсчета.
Траектория движения материальной точки – линия, описываемая этой точкой в пространстве.
Направление вектора средней скорости совпадает с направлением
Средним ускорением неравномерного движения в интервале от t до Мгновенным ускорением a (ускорением) материальной точки в момент времени t будет предел среднего ускорения:
|
|||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-14; просмотров: 746; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.86.209 (0.015 с.) |

 Вектор
Вектор  , т. е. приращение радиус-вектора точки за рассматриваемый промежуток времени, называется перемещением.
, т. е. приращение радиус-вектора точки за рассматриваемый промежуток времени, называется перемещением.
 Длина участка траектории АВ, пройденного материальной точкой с момента начала отсчета времени, называется длиной пути
Длина участка траектории АВ, пройденного материальной точкой с момента начала отсчета времени, называется длиной пути 
 Вектором средней скорости < v > называется отношение приращения
Вектором средней скорости < v > называется отношение приращения  радиус-вектора точки к промежутку времени
радиус-вектора точки к промежутку времени  :
: . При неограниченном уменьшении
. При неограниченном уменьшении  средняя скорость стремится к предельному значению, которое называется мгновенной скоростью v:
средняя скорость стремится к предельному значению, которое называется мгновенной скоростью v:

 называется векторная величина, равная отношению изменения скорости
называется векторная величина, равная отношению изменения скорости  к интервалу времени
к интервалу времени 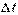 :
: 

 Угловой скоростью называется векторная величина, равная первой производной угла поворота тела по времени:
Угловой скоростью называется векторная величина, равная первой производной угла поворота тела по времени:
 Вектор
Вектор  так же, как и вектор
так же, как и вектор  . Размерность угловой скорости
. Размерность угловой скорости  , а ее единица – радиан в секунду (рад/с).
, а ее единица – радиан в секунду (рад/с).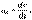
 и
и 
 .
. нормальное ускорение
нормальное ускорение 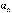 ) и угловыми величинами (угол поворота
) и угловыми величинами (угол поворота  , угловая скорость
, угловая скорость  , угловое ускорение
, угловое ускорение  ) выражается следующими формулами:
) выражается следующими формулами:  ,
,  ,
,  ,
,  .
.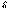 =const)
=const) 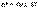 ,
,  где
где  – начальная угловая скорость.
– начальная угловая скорость.

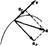 Полное ускорение тела есть геометрическая сумма тангенциальной и нормальной составляющих (рис. 1.5):
Полное ускорение тела есть геометрическая сумма тангенциальной и нормальной составляющих (рис. 1.5):
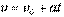 Равнопеременное движение
Равнопеременное движение 
 ,
,  – прямолинейное равномерное движение;
– прямолинейное равномерное движение; ,
, 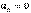 – прямолинейное равнопеременное движение.
– прямолинейное равнопеременное движение. ,
, 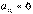 – прямолинейное движение с переменным ускорением;
– прямолинейное движение с переменным ускорением;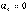 ,
,  . При
. При  скорость по модулю не изменяется, а изменяется по направлению.
скорость по модулю не изменяется, а изменяется по направлению. ,
,  – равномерное криволинейное движение;
– равномерное криволинейное движение;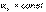 ,
, 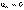 – криволинейное равнопеременное движение;
– криволинейное равнопеременное движение; ,
, 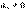 – криволинейное движение с переменным ускорением.
– криволинейное движение с переменным ускорением.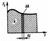
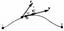 где – угол между векторами F и d r; ds =| d r | – элементарный путь; F s – проекция вектора F на вектор d r
где – угол между векторами F и d r; ds =| d r | – элементарный путь; F s – проекция вектора F на вектор d r
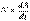


 -собственная частота свободных незатухающих колебаний(-сколько раз за p секунд тело пройдет через положение равновесия)
-собственная частота свободных незатухающих колебаний(-сколько раз за p секунд тело пройдет через положение равновесия) Решение уравнения - х(t)=а0е- btcos( wt+a) a-начальная фаза.
Решение уравнения - х(t)=а0е- btcos( wt+a) a-начальная фаза. называется логарифмическим декрементом затухания
называется логарифмическим декрементом затухания
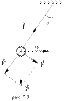
 , направленная вдоль нити, не учитывается, т.к. уравновешивается силой натяжения нити. При малых углах смещения
, направленная вдоль нити, не учитывается, т.к. уравновешивается силой натяжения нити. При малых углах смещения  и, тогда координату х можно отсчитывать по горизонтальному направлению. Из рис.7.3 видно, что составляющая веса, перпендикулярная нити, равна
и, тогда координату х можно отсчитывать по горизонтальному направлению. Из рис.7.3 видно, что составляющая веса, перпендикулярная нити, равна

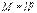 , и момент инерции:
, и момент инерции:


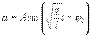 ,
, и
и 


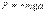
 . Момент силы: определить в явном виде нельзя. С учетом всех величин, входящих в исходное дифференциальное уравнение колебаний физического маятника имеет вид:
. Момент силы: определить в явном виде нельзя. С учетом всех величин, входящих в исходное дифференциальное уравнение колебаний физического маятника имеет вид: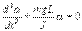


 или
или .
.
 ,
,



