
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Законы динамики. Основное уравнение динамики точки.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Законы динамики. Основное уравнение динамики точки. 1-й закон динамики (закон инерции): всякое, изолированное от внешних воздействий тело, сохраняет состояние покоя или равномерного прямолинейного движения до тех пор, пока воздействие со стороны других тел не выведут его из этого состояния. 2-й закон динамики (основной): ускорение, сообщаемое м.т. силой, прямопропорционально величине этой силы и совпадает с ней по направлению. F=ma a=F/m 3-й закон динамики (закон взаимодействия): силы взаимодействия между собой двух тел равны по модулю и направлены по одной прямой в противоположные стороны. F12=-F21 4-й закон динамики (принцип независимости действия сил): ускорение сообщаемое м.т. равнодействующей силой равно геометрической сумме ускорений, которые получила бы точка от действия каждой из сил по отдельности. Я и 2-я основные задачи динамики и методы их решения. 1-я задача (прямая): по известной массе точки и кинематическим характеристикам движения определяется действующая сила (решается дифференцированием кинематического уравнения движения) 2-я задача (обратная): по известным, массе точки, действующим силам и начальным условиям движения определить кинематические характеристики (решается интегрированием ДУ движения) Дифференциальные уравнения движения точки в декартовых и естественных осях координат.
Дифференциальные уравнения движения несвободной материальной точки в форме Эйлера. Если точка является несвободной (на движение точки наложены связи), в число действующих на точку сил включаются реакции связей.
Силы, входящие в правую часть дифференциальных уравнений движения, в общем случае могут являться функциями от времени t, скорости v и координат х, у, z точки.
Прямолинейное движение материальной точки. Равномерным прямолинейным движением называется движение, при котором материальная точка за любые равные промежутки времени совершает одинаковые перемещения. Уравнение такого движения в векторной форме записывается так:
где При прямолинейном движении ось координат направлена по направлению движения точки, в результате чего из 3-х ДУ остаётся одно: Интегрирование ДУ движения в случаях, когда сила зависит от скорости, времени, координаты. Интегрирование ДУ движения для случая F = F (t) Уравнение задачи Коши с помощью первой подстановки a = dv / dt приводится к системе двух ДУ. получим первый интеграл – закон изменения скорости и второй интеграл – закон движения: v = v 0 + (1/ m) x = x 0 +v 0 t + (1/ m)
Интегрирование ДУ движения для случая F = F (x)
Уравнение задачи Коши с помощью второй подстановки a = vdv / dx позволяет получить первый интеграл
и второй – аналогичный:
Интегрирование ДУ движения для случая F = F (v) В этом случае рекомендуется пользоваться следующим правилом: Если в задаче дано или нужно найти время t,применять первую подстановку a = dv / dt. Если в задаче можно обойтись без определения времени, следует применять вторую подстановку a = vdv / dx. Масса системы. Центр масс, определение его положения. Положение центра масс при наличии оси или плоскости симметрии. Понятие о центре тяжести. Масса системы равна алгебраической сумме масс точек или тел её составляющих. Положение центра масс системы определяется радиусом-вектором либо координатами.
Координаты центра масс определяются с помощью этой же формулы относительно (x,y,z)
Центр тяжести- точка пересечения осей, статический момент которой равен нулю. Центр тяжести двух материальных точек имеет весьма простой механический смысл. Представим себе жёсткий “невесомый” стержень АВ, в концах которого помещены массы а и b. “Невесомость” стержня практически означает, что его масса по сравнению с массами a и b настолько незначительна, что ею можно пренебречь. Центр тяжести С материальных точек (A, a) и (B, b) — это такая точка, в которой надо подпереть стержень AB, чтобы он был в равновесии.
Принцип Даламбера для механической системы. Принцип Даламбера для материальной точки. Примеры. При движении механической системы главный вектор и главный момент внешних сил относительно произвольного центра как бы устанавливается главным вектором и главным моментом относительно того же центра сил инерции. ∑Fke+Ru=0 ∑M0(Fke)+M0u=0 Принцип Даламбера устанавливает единый подход к исследованию движения любой механической системы вне зависимости от характера налагаемых на это движение условий. При этом динамическим дифференциальным уравнениям движения придается вид уравнений равновесия. Рассмотрим несвободную материальную точку М, движущуюся по кривой АВ под действием активных сил, равнодействующая которых равна F. Обозначив через N силу реакции, с которой кривая АВ действует на точку М, запишем основное уравнение динамики точки/ Силы F, N, Ф образуют сходящуюся систему сил и полученное уравнение выражает условие равновесия этой системы, что и составляет принцип Даламбера для материальной точки.
Сила инерции равна произведению массы тела на его ускорение и направлена противоположно ускорению. Ф=-ma
Законы динамики. Основное уравнение динамики точки. 1-й закон динамики (закон инерции): всякое, изолированное от внешних воздействий тело, сохраняет состояние покоя или равномерного прямолинейного движения до тех пор, пока воздействие со стороны других тел не выведут его из этого состояния. 2-й закон динамики (основной): ускорение, сообщаемое м.т. силой, прямопропорционально величине этой силы и совпадает с ней по направлению. F=ma a=F/m 3-й закон динамики (закон взаимодействия): силы взаимодействия между собой двух тел равны по модулю и направлены по одной прямой в противоположные стороны. F12=-F21 4-й закон динамики (принцип независимости действия сил): ускорение сообщаемое м.т. равнодействующей силой равно геометрической сумме ускорений, которые получила бы точка от действия каждой из сил по отдельности.
|
||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 1457; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.108 (0.006 с.) |


 - ДУ движения несвободной м.т. в декартовых координатах
- ДУ движения несвободной м.т. в декартовых координатах
 - главный вектор (геом. Сумма действующих на точку активных сил)
- главный вектор (геом. Сумма действующих на точку активных сил)
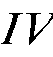 - равнодействующая реакция связи
- равнодействующая реакция связи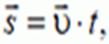
 — перемещение,
— перемещение,  — скорость движения, t — время.
— скорость движения, t — время.
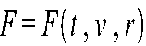
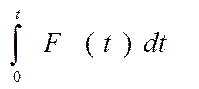 ,
,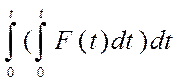 .
.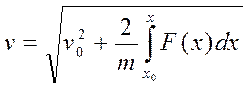
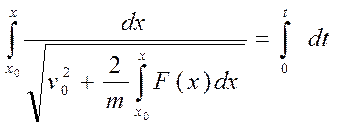
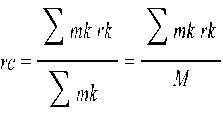 , где rk – радиус-вектор k-той точки или системы
, где rk – радиус-вектор k-той точки или системы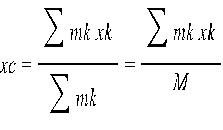
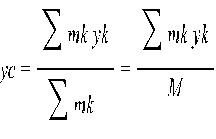
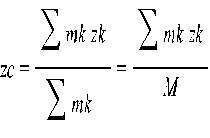
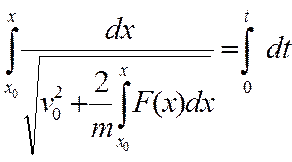 При движении материальной точки векторная сумма действующих на ней активных сил, равнодействующих реакций и сила инерции будет равна нулю.
При движении материальной точки векторная сумма действующих на ней активных сил, равнодействующих реакций и сила инерции будет равна нулю.


