
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Уравнение Лагранжа 2-го рода для консервативных систем. Кинетический потенциал.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Функция L=T-П – кинетический потенциал.
Основные гипотезы элементарной теории удара. Теорема об изменении количества движения и момента количества движения при ударе. Ударом называется такое явление при котором скорости точек тела за бесконечно малый промежуток времени меняется на конечную величину. Время за которое это происходит называется временем удара. В теории удара рассматриваются не ударные силы а ударные импульсы. mv-mu=∑Ske - Теорема об изменении количества движения Теорема об изменении количества движения точки при ударе.
Коэффициент восстановления. Экспериментальное определение. Одним из способов определения коэффициента восстановления при ударе может служить определение высоты отскока шара от неподвижной поверхности, падающего на нее с высоты K=U/v – коофициент восстановления К=0 –неупругий удар К=1 – обсалютно упругий удар 0<K<1 – упругий удар
Упругий и неупругий удар. Прямой и косой удар по гладкой поверхности. Прямой удар двух шаров. Взаимодействие тел, при котором за малый промежуток времени скорости точек изменяются на конечную величину, называется ударом. Силы, возникающие при таком взаимодействии, называются ударными. Из теоремы об изменении количества движения следует, что импульс этих сил за время удара есть конечная величина Прямой центральный удар двух тел. Удар называется прямым и центральным, если центры масс тел до удара двигались по одной прямой, по оси х, точка встречи их поверхностей оказывается на этой же прямой и общая касательная Т к поверхностям будет перпендикулярна оси х (рис.112).
Если касательная Т не перпендикулярна этой оси, удар называется косым Пусть тела двигались поступательно со скоростями их центров масс За время удара
где
Теорема об изменении кинетической энергии при ударе (теорема Карно). Действие ударной нагрузки на вращающееся тело. Центр удара. Теорема об изменении кинетического момента механической системы при ударе. При неупругом ударе в механической системе потеря кинетической энергии равна кинетической энергии данной системы, если бы она двигалась с потерянными скоростями.Изменение кинетического момента механической системы относительно любого неподвижного центра за время удара равно сумме моментов всех внешних ударных импульсов, приложенных к точкам системы, относительно этого же центра.
Первая теорема Карно Потерянная кинетическая энергия равна энергии точки массой разности скоростей точек до удара: Центр удара - это точка вращающегося тела, при действии на которую ударного импульса, не возникают ударные реакции. Если что такая точка существует. Для того чтобы при действии ударного импульса на вращающееся тело в подшипниках не возникали ударные реакции, надо, чтобы выполнялись условия: Центр удара лежит в плоскости, проходящей через центр масс и ось вращения, на расстоянии Ударный импульс направлен перпендикулярно этой плоскости. Ось вращения является главной для точки ее пересечения с плоскостью действия ударного импульса. Законы динамики. Основное уравнение динамики точки.
|
||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 885; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.108 (0.007 с.) |

 (
( )-
)-  =
=  - Уравнение Лагранжа 2-го рода для консервативных систем
- Уравнение Лагранжа 2-го рода для консервативных систем =∑M0(Fke) – относительно точки
=∑M0(Fke) – относительно точки =∑Mz(Fke) – относительно оси
=∑Mz(Fke) – относительно оси без начальной скорости. Скорость шара в начале удара
без начальной скорости. Скорость шара в начале удара  . В конце удара
. В конце удара  , где
, где  − высота, на которую шар поднимется после удара. Тогда:
− высота, на которую шар поднимется после удара. Тогда: 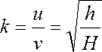

 и
и  . Определим каковы будут их скорости
. Определим каковы будут их скорости  и
и  после удара.
после удара. на тела действуют ударные силы
на тела действуют ударные силы  , импульсы
, импульсы  которых, приложенные в точке касания, показаны на рис.112,б. По теореме об изменении количества движения, в проекциях на ось х, получим два уравнения
которых, приложенные в точке касания, показаны на рис.112,б. По теореме об изменении количества движения, в проекциях на ось х, получим два уравнения (1)
(1) и
и  - массы тел;
- массы тел; 


 - проекции скоростей на ось х.
- проекции скоростей на ось х.
 , которая движется со скоростью, равной
, которая движется со скоростью, равной . М называется в механике приведенной массой системы.
. М называется в механике приведенной массой системы. .Для системы координат с началом в точке
.Для системы координат с началом в точке  и направлением оси
и направлением оси  таким образом, чтобы она проходила через точку приложения ударного импульса, то для обращения в ноль импульсов реакций необходимо
таким образом, чтобы она проходила через точку приложения ударного импульса, то для обращения в ноль импульсов реакций необходимо  , т.е. ось
, т.е. ось  должна быть главной осью инерции для точки
должна быть главной осью инерции для точки  .
. от оси.
от оси.


