
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Свободные колебания точки , частота и период колебания.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Влияние постоянной силы на свободные колебания. Определение эквивалентной жесткости при последовательном и параллельном соединении пружин. Постоянная действующая сила не влияет на характер колебательного движения, но вызывает смещение равновесного состояния на величину fcm. Последовательное соединение: Паралельное соединение: 10. Колебания при наличии сил вязкого трения (затухающие колебания). Декремент колебаний. Апериодическое движение.
k - циклическая частота колебаний. n - коэффициент учитывающий сопротивление.
11. Вынужденные колебания материальной точки. Явление резонанса. Коэффициент динамичности. Поведение системы в околорезонансной зоне. Биение. Вынужденные колебания будут происходить если на точку помимо востонавливающей силы действует сила периодического характера – возмущающая сила. Появление возмущающей силы может возникать при непосредственной её приложении к движущей точке (силовое возбуждение и действий на основание к которому точка прикреплена кинимотическое возбуждение) В случае когда возмущающая сила Р меньше частоты свободных колебаний то колебания происходят с малой частотой. Если Р > K – вынужденные колебания большой частоты. Отношение амплитуды вынужденных колебаний А к статической деформации называется коофициентом динамичности.Η=А/fct= В случаях когда частота свободных колебаний близка к возмущающей силе возникает биение. Если частота собственных колебаний совпадает с частотой собственной силы возникает резонанс.
12. Вынужденные колебания при наличии вязкого сопротивления. Коэффициент динамичности. Сдвиг фаз. Коэффициентом динамичности в теории колебаний называют безразмерную скалярную физическую величину, определяемую следующим выражением:
где А — амплитуда А_0 — равновесная амплитуда представляющая собой статическую деформацию упругой связи под действием максимальной силы P_0 ω — частота возмущения p — собственная частота колебаний n — коэффициент, характеризующий силы вязкого трения Непосредственное определение коэффициента n, затруднительно. Поэтому в формулу (1) целесообразно вместо n ввести коэффициент поглощения ψ. Тогда
Преимуществом формулы (2) является, то что коэффициент динамичности ставиться в зависимость от энергетической характеристики трения ψ, что позволяет использовать эту формулу не только для вязкого трения, но и для других законов трения. Сдвиг фаз — разность между начальными фазами двух переменных величин, изменяющихся во времени периодически с одинаковой частотой. Сдвиг фаз является величиной безразмерной и может измеряться в градусах, радианах или долях периода. В электротехнике сдвиг фаз между напряжением и током определяет коэффициент мощности в цепях переменного тока. вынужденные колебания ПРИ НАЛИЧИИ ВЯЗКОГО СОПРОТИВЛЕНИЯ СРЕДЫ
13. Понятие о механической системе. Основные определения. Свойства внутренних сил механической системы. Система – совокупность тел, связанных между собой. Силы, действующие на тела системы делятся на внешние и внутренние. Внешние ( Свойства внутренних сил: 1) главный вектор (геом.сумма) и сумма проекций всех внутренних сил на произвольно выбранной оси координат равны нулю. 2) главный момент (геометрическая сумма моментов) действующих внутренних сил относительно произвольного центра и сумма моментов внутренних сил относительно произвольных осей координат равны нулю. 3)система м.т. на которую не налагаются внешние связи называется свободной, в любом другом случае система является несвободной.
|
||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 926; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.008 с.) |

 - ДУ свободных колебаний
- ДУ свободных колебаний  - циклическая частота
- циклическая частота  - период
- период




 - ДУ затухающих колебаний при силе сопротивления прямопропорц. скорости.
- ДУ затухающих колебаний при силе сопротивления прямопропорц. скорости. - декремент колебаний
- декремент колебаний 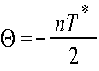 - показ. насколько быстро измен. амплитуда колебаний
- показ. насколько быстро измен. амплитуда колебаний - такое движение наз. апериодическим
- такое движение наз. апериодическим


 ) – называются силы взаимодействия между телами данной системы и телами, которые в данную систему не входят. Внутренние (
) – называются силы взаимодействия между телами данной системы и телами, которые в данную систему не входят. Внутренние ( ) – наз. Силы взаимодействия между телами. Одна и та же сила может быть одновременно и внешней и внутренней, в зависимости от того какая система рассматривается.
) – наз. Силы взаимодействия между телами. Одна и та же сила может быть одновременно и внешней и внутренней, в зависимости от того какая система рассматривается.


