
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Сложение гармонических колебаний одного направления и одинаковой частоты. Биения.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Пусть совершаются два гармонических колебания одного направления и одинаковой частоты
Уравнение результирующего колебания будет иметь вид
Убедимся в этом, сложив уравнения системы (4.1)
Применив теорему косинусов суммы и сделав алгебраические преобразования:
Можно найти такие величины А и φ0, чтобы удовлетворялись уравнения
Рассматривая (4.3) как два уравнения с двумя неизвестными А и φ0, найдем, возведя их в квадрат и сложив, а затем разделив второе на первое:
Подставляя (4.3) в (4.2), получим:
Или окончательно, используя теорему косинусов суммы, имеем:
Тело, участвуя в двух гармонических колебаниях одного направления и одинаковой частоты, совершает также гармоническое колебание в том же направлении и с той же частотой, что и складываемые колебания. Амплитуда результирующего колебания зависит от разности фаз (φ2-φ1) сгладываемых колебаний. В зависимости от разности фаз (φ2-φ1): 1) (φ2-φ1) = ±2mπ (m=0, 1, 2, …), тогда A= А1+А2, т. е. амплитуда результирующего колебания А равна сумме амплитуд складываемых колебаний; 2) (φ2-φ1) = ±(2m+1)π (m=0, 1, 2, …), тогда A= |А1-А2|, т. е. амплитуда результирующего колебания равна разности амплитуд складываемых колебаний
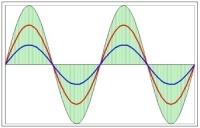
Периодические изменения амплитуды колебания, возникающие при сложении двух гармонических колебаний с близкими частотами, называются биением. Пусть два колебания мало отличаются по частоте. Тогда амплитуды складываемых колебаний равны А, а частоты равны ω и ω+Δω, причем Δω намного меньше ω. Начало отсчета выберем так, чтобы начальные фазы обоих колебаний были равны нулю:
Решим систему
Решение системы:
Результирующее колебание можно рассматривать как гармоническое с частотой ω, амплитуда А, которого изменяется по следующему периодическому закону:
Частота изменения А в два раза больше частоты изменения косинуса. Частота биений равна разности частот складываемых колебаний: ωб = Δω Период биений:
Определение частоты тона (звука определенной высоты биений эталонным и измеряемым колебаниями — наиболее широко применяемый на метод сравнения измеряемой величины с эталонной. Метод биений используется для настройки музыкальных инструментов, анализа слуха и т. д.
4. Затухающие колебания и их характеристики: амплитуда, частота, коэффициент затухания, логарифмический декремент затухания. Свободные колебания технических систем в реальных условиях протекают, когда на них действуют силы сопротивления. Действие этих сил приводит к уменьшению амплитуды колеблющейся величины. Колебания, амплитуда которых из-за потерь энергии реальной колебательной системы уменьшается с течением времени, называются затухающими. Наиболее часто встречается случаи, когда сила сопротивления пропорциональна скорости движения
где r - коэффициент сопротивления среды. Знак минус показывает, что FC направлена в сторону противоположную скорости. Запишем уравнение колебаний в точке, колеблющийся в среде, коэффициент сопротивлений которой r. По второму закону Ньютона
где β - коэффициент затухания. Этот коэффициент характеризует скорость затухания колебаний, При наличии сил сопротивления энергия колеблющейся системы будет постепенно убывать, колебания будут затухать. дифференциальное уравнение затухающих колебаний: уравнение затухающих колебаний: ω – частота затухающих колебаний: Период затухающих колебаний: Затухающие колебания при строгом рассмотрении не являются периодическими. Поэтому о периоде затухаюших колебаний Если затухания выражены слабо (β→0), то рассматривать как гармонические колебания, амплитуда которых меняется по экспоненциальному закону
В уравнении (1) А0 и φ0 - произвольные константы, зависящие от выбора момента времени, начиная е которого мы рассматриваем колебания
Коэффициент затихания β обратно пропорционален времени, в течение которого амплитуда уменьшается в е раз. Однако коэффициента затухания недостаточна для характеристики затуханий колебаний. Поэтому необходимо ввести такую характеристику для затухания колебаний, в которую входит время одного колебаний. Такой характеристикой является декремент (по-русски: уменьшение) затухания D, который равен отношению амплитуд, отстоящих по времени на период: Логарифмический декремент затухания равен логарифму D: Логарифмический декремент затухания обратно пропорционален числу колебаний, в результате которых амплитуда колебаний уменьшилась в е раз. Логарифмический декремент затухания - постоянная для данной системы величина. Еще одной характеристикой колебательной система является добротность Q.
Добротность пропорциональна числу колебаний, совершаемых системой, за время релаксации τ. Добротность Q колебательной системы является мерой относительной диссипации (рассеивания) энергии. Добротность Q колебательной системы называется число, показывающее во сколько раз сила упругости больше силы сопротивления.
Чем больше добротность, тем медленнее происходит затухание, тем затухающие колебания ближе к свободным гармоническим.
|
||||
|
Последнее изменение этой страницы: 2016-07-16; просмотров: 655; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.141.46.108 (0.007 с.) |

 (4.1)
(4.1)

 (4.2)
(4.2)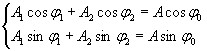 (4.3)
(4.3)







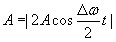

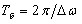
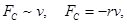
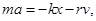



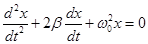


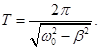
 можно говорить, когда β мало.
можно говорить, когда β мало. Затухающие колебания можно
Затухающие колебания можно
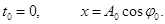

 ;
; 





