
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вынужденные колебания. Амплитуда и фаза вынужденных синусоидальных колебаний. Резонанс. Резонансные кривые.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Вынужденные колебания — колебания, происходящие под воздействием внешних периодических сил. Наиболее простой и содержательный пример вынужденных колебаний можно получить из рассмотрения гармонического осциллятора и вынуждающей силы, которая изменяется по закону: ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ, колебания, возникающие в какой-либо системе в результате периодически изменяющегося внешнего воздействия: силы в механической системе, напряжения или тока в колебательном контуре. Вынужденные колебания всегда происходят с частотой, равной частоте внешнего воздействия; в системе при определенных условиях возможен резонанс. Вынужденные колебания полностью устанавливаются в системе лишь после того, как в ней затухнут также вызванные внешним воздействием собственные колебания. Примеры вынужденных колебаний: колебания мембраны телефона, иглы швейной машины, поршня в цилиндре автомобильного двигателя, рессор автомобиля, движущегося по неровной дороге, океанические приливы под действием Луны и др. Резонанс — элементарная частица, представляющая собой возбуждённое состояние адрона. Большинство известных частиц являются резонансами. Посередине графика виден пик, отвечающий ипсилон-резонансу Время жизни резонансов: 10−22—10−24 с, поэтому их невозможно наблюдать непосредственно в виде треков на детекторах. Они определяются как пики в полном сечении образованиявторичных частиц:
Максимальное сечение
Резонансы аналогичны возбуждённым состояниям атома: когда электрон поглощает энергию и переходит на другой более высокий энергетический уровень. Подобные возбуждённые состояния, называемые изомерами, существуют и у атомных ядер. Аналогично электрону в атоме или нуклону в ядре, кварки, получая достаточную порцию энергии, также переходят на другой энергетический уровень. Обычные же (метастабильные) частицы при этом являются основными состояниями кварковой системы. Соответственно, резонансы можно описыватьспектральными термами · · · · В отличие от электрического поля внутри атома, теория которого довольно проста, кварки находятся в глюонном поле, а описание представляет довольно большую сложность. Поэтому невозможно заранее предсказать спектр возбуждения кварковой системы. В связи с этим каждый новый резонанс до сих пор является своего рода сюрпризом для физиков. Сложность представляет даже отделение чистых Резона́нс (фр. resonance, от лат. resono — откликаюсь) — явление резкого возрастания амплитуды вынужденных колебаний, которое наступает при приближениичастоты внешнего воздействия к некоторым значениям (резонансным частотам), определяемым свойствами системы. Увеличение амплитуды — это лишь следствие резонанса, а причина — совпадение внешней (возбуждающей) частоты с внутренней (собственной) частотой колебательной системы. При помощи явления резонанса можно выделить и/или усилить даже весьма слабые периодические колебания. Резонанс — явление, заключающееся в том, что при некоторой частоте вынуждающей силы колебательная система оказывается особенно отзывчивой на действие этой силы. Степень отзывчивости в теории колебаний описывается величиной, называемойдобротность. Явление резонанса впервые было описано Галилео Галилеем в 1602 г в работах, посвященных исследованию маятников и музыкальных струн.[1][2] Наиболее известная большинству людей механическая резонансная система — это обычные качели. Если вы будете подталкивать качели в соответствии с их резонансной частотой, размах движения будет увеличиваться, в противном случае движения будут затухать. Резонансную частоту такого маятника с достаточной точностью в диапазоне малых смещений от равновесного состояния, можно найти по формуле:
где g это ускорение свободного падения (9,8 м/с² для поверхности Земли), а L — длина от точки подвешивания маятника до центра его масс. (Более точная формула довольно сложна, и включает эллиптический интеграл). Важно, что резонансная частота не зависит от массы маятника. Также важно, что раскачивать маятник нельзя на кратных частотах (высших гармониках), зато это можно делать на частотах, равных долям от основной (низших гармониках). Резонансные явления могут вызвать необратимые разрушения в различных механических системах. В основе работы механических резонаторов лежит преобразование потенциальной энергии в кинетическую. В случае простого маятника, вся его энергия содержится в потенциальной форме, когда он неподвижен и находится в верхних точках траектории, а при прохождении нижней точки на максимальной скорости, она преобразуется в кинетическую. Потенциальная энергия пропорциональна массе маятника и высоте подъёма относительно нижней точки, кинетическая — массе и квадрату скорости в точке измерения. Другие механические системы могут использовать запас потенциальной энергии в различных формах. Например, пружина запасает энергию сжатия, которая, фактически, является энергией связи её атомов.
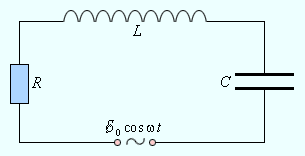
Вынужденные колебания в последовательном RLС-контуре под действием синусоидальной электродвижущей силы. Векторная диаграмма напряжений. Полное сопротивление контура переменному току. Амплитуда и фаза вынужденных колебаний. Резонансные кривые. Процессы, возникающие в электрических цепях под действием внешнего периодического источника тока, называются вынужденными колебаниями. Вынужденные колебания, в отличие от собственных колебаний в электрических цепях, являются незатухающими. Внешний источник периодического воздействия обеспечивает приток энергии к системе и не дает колебаниям затухать, несмотря на наличие неизбежных потерь. Особый интерес представляет случай, когда внешний источник, напряжение которого изменяется по гармоническому закону с частотой ω, включен в электрическую цепь, способную совершать собственные свободные колебания на некоторой частоте ω0. Если частота ω0 свободных колебаний определяется параметрами электрической цепи, то установившиеся вынужденные колебания всегда происходят на частоте ω внешнего источника. Для установления вынужденных стационарных колебаний после включения в цепь внешнего источника необходимо некоторое время Δt. Это время по порядку величины равно времени τ затухания свободных колебаний в цепи. Электрические цепи, в которых происходят установившиеся вынужденные колебания под действием периодического источника тока, называются цепями переменного тока. Рассмотрим последовательный колебательный контур, то есть RLC-цепь, в которую включен источник тока, напряжение которого изменяется по периодическому закону (рис. 2.3.1): e (t) = e0cos ωt, где e0 – амплитуда, ω – круговая частота.
Рисунок 2.3.1.Вынужденные колебания в контуре Предполагается, что для электрической цепи, изображенной на рис. 2.3.1, выполнено условие квазистационарности. Поэтому для мгновенных значений токов и напряжений можно записать закон Ома: Теперь можно построить векторную диаграмму для последовательного RLC-контура, в котором происходят вынужденные колебания на частоте ω. Поскольку ток, протекающий через последовательно соединенные участки цепи, один и тот же, векторную диаграмму удобно строить относительно вектора, изображающего колебания тока в цепи. Амплитуду тока обозначим через I0. Фаза тока принимается равной нулю. Это вполне допустимо, так как физический интерес представляют не абсолютные значения фаз, а относительные фазовые сдвиги. Векторная диаграмма для последовательного RLC-контура изображена на рис. 2.3.2.
Векторная диаграмма на рис. 2.3.2 построена для случая, когда Из рисунка видно, что Из выражения для I0 видно, что амплитуда тока принимает максимальное значение при условии
Явление возрастания амплитуды колебаний тока при совпадении частоты ω колебаний внешнего источника с собственной частотой ω0 электрической цепи называется электрическим резонансом. При резонансе При последовательном резонансе (ω = ω0) амплитуды UC и UL напряжений на конденсаторе и катушке резко возрастают: понятие добротности RLC-контура:
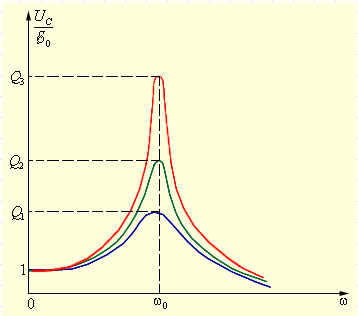
Рисунок 2.3.4. Резонансные кривые для контуров с различными значениями добротности Q. Рис. 2.3.4 иллюстрирует явление резонанса в последовательном электрическом контуре. На рисунке графически изображена зависимость отношения амплитуды UC напряжения на конденсаторе к амплитуде е0 напряжения источника от его частоты ω для различных значений добротности Q. Кривые на рис. 2.3.3 называются резонансными кривыми. Полное сопротивление: Если в цепи переменного тока имеются нагрузки разных типов, то закон Ома выполняется только для максимальных (амплитудных) и действующих значений тока и напряжения. читывая, что отношение напряжения к силе тока – это сопротивление, и подставляя конкретные выражения для соответствующих сопротивлений, получим:
|
||||
|
Последнее изменение этой страницы: 2016-07-16; просмотров: 2977; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.43.200 (0.013 с.) |

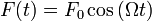 .
.
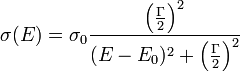
 соответствует резонансу с энергией
соответствует резонансу с энергией  и шириной
и шириной  . Ширина резонанса, выражаемая в единицах энергии соответствует его среднему времени жизни
. Ширина резонанса, выражаемая в единицах энергии соответствует его среднему времени жизни 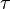

 , где:
, где: — главное квантовое число,
— главное квантовое число, — спиновое квантовое число (0 или 1 — для мезонов, 1⁄2 или 3⁄2 — для барионов),
— спиновое квантовое число (0 или 1 — для мезонов, 1⁄2 или 3⁄2 — для барионов), — орбитальное квантовое число,
— орбитальное квантовое число,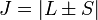 — внутреннее квантовое число (соответствует спину самого резонанса).
— внутреннее квантовое число (соответствует спину самого резонанса). и
и  состояний от систем с дополнительными кварками (тетракварк, пентакварк) и глюонной примесью (глюбол).
состояний от систем с дополнительными кварками (тетракварк, пентакварк) и глюонной примесью (глюбол).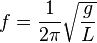 ,
, -
-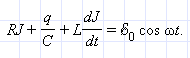 . Величина
. Величина 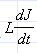 -это ЭДС самоиндукции катушки, перенесенная с изменением знака из правой части уравнения в левую. Эту величину принято называть напряжением на катушке индуктивности. Уравнение вынужденных колебаний можно записать в виде: uR + uC + uL = e (t) = e0 cos ωt, где uR (t), uC (t) и uL (t) – мгновенные значения напряжений на резисторе, конденсаторе и катушке соответственно. Амплитуды этих напряжений будем обозначать буквами UR, UC и UL. При установившихся вынужденных колебаниях все напряжения изменяются с частотой ω внешнего источника переменного тока
-это ЭДС самоиндукции катушки, перенесенная с изменением знака из правой части уравнения в левую. Эту величину принято называть напряжением на катушке индуктивности. Уравнение вынужденных колебаний можно записать в виде: uR + uC + uL = e (t) = e0 cos ωt, где uR (t), uC (t) и uL (t) – мгновенные значения напряжений на резисторе, конденсаторе и катушке соответственно. Амплитуды этих напряжений будем обозначать буквами UR, UC и UL. При установившихся вынужденных колебаниях все напряжения изменяются с частотой ω внешнего источника переменного тока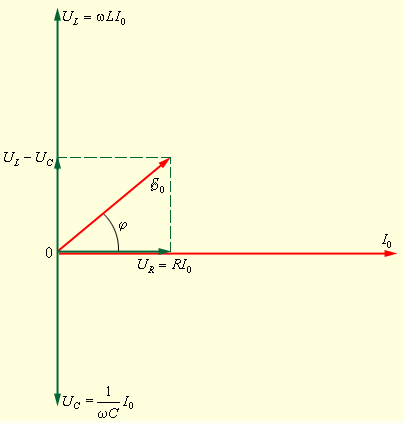 - Рисунок 2.3.3.Векторная диаграмма для последовательной RLC-цепи
- Рисунок 2.3.3.Векторная диаграмма для последовательной RLC-цепи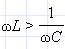 или
или 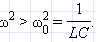 В этом случае напряжение внешнего источника опережает по фазе ток, текущий в цепи, на некоторый угол φ.
В этом случае напряжение внешнего источника опережает по фазе ток, текущий в цепи, на некоторый угол φ.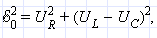 откуда следует
откуда следует 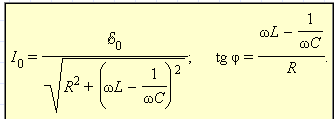
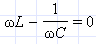 или
или 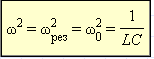
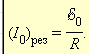 Сдвиг фаз φ между приложенным напряжением и током в цепи при резонансе обращается в нуль. Резонанс в последовательной RLC-цепи называется резонансом напряжений. Аналогичным образом с помощью векторной диаграммы можно исследовать явление резонанса при параллельном соединении элементов R, L и C (так называемый резонанс токов).
Сдвиг фаз φ между приложенным напряжением и током в цепи при резонансе обращается в нуль. Резонанс в последовательной RLC-цепи называется резонансом напряжений. Аналогичным образом с помощью векторной диаграммы можно исследовать явление резонанса при параллельном соединении элементов R, L и C (так называемый резонанс токов).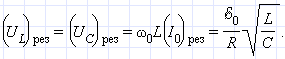
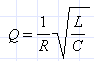
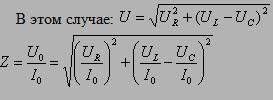
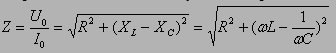 (2)
(2)


