
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Превращения энергии при вынужденных колебаниях.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Внешняя сила, действующая на колебательную систему, совершает работу, следовательно, в систему поступает энергия. Полезно рассмотреть превращения энергии в ходе вынужденных колебаний. Для этого поступим уже традиционным образом: динамическое уравнение[6] колебаний
умножим на скорость
и перепишем в виде
В этом уравнении каждое слагаемое имеет наглядный физический смысл. Так функция Слагаемое
и равно скорости изменения кинетической энергии колеблющегося тела Δ E kin. Наконец,
есть мощность силы упругости, равная скорости изменения потенциальной энергии системы U. С учетом проведенных преобразований, уравнение (2) приобретает смысл закона сохранения и превращения энергии:
энергия, переданная посредством работы внешней силы, расходуется на увеличение механической энергии системы и работу против сил сопротивления (равную в свою очередь, потерям механической энергии). Полученное уравнение (3) справедливо для любого промежутка времени, в том числе и на стадии переходного режима. Применим его к режиму установившихся колебаний. В этом режиме колебания являются гармоническими, поэтому за время равное периоду колебаний все характеристики движения (координата, скорость, кинетическая и потенциальная энергия) возвращаются к исходным значениям. Если в уравнении (3) интервал времени Δ t положить равным периоду колебаний, то изменение полной энергии будет равно нулю, что приводит к очевидному результату: работа внешней силы за период колебаний равна работе против силы сопротивления. Иными словами, вся энергия, поступающая в систему, превращается в теплоту, выделяющуюся из-за наличия сил сопротивления. Не составляет труда получить точные значения механической энергии и мощностей всех сил в процессе вынужденных колебаний. Зависимости координаты и скорости от времени нам известны и описываются формулами
В этом режиме полная механическая энергия системы равна
Ее значение колеблется вокруг некоторого среднего значения. Мощности внешней силы и силы сопротивления описываются формулами
Причем первая принимает как положительные, так и отрицательные значения, а вторая все время положительна.
На рисунке 232 показаны графики зависимостей от времени внешней силы, координаты и скорости частицы, ниже построены графики зависимости от времени мощностей внешней силы и силы сопротивления, а также механической энергии. Графики построены для случая, когда частота вынуждающей силы меньше собственной частоты системы ω < ω 0, а затухание незначительно. На графиках выделены интервалы времени, когда работа внешней силы положительна, то есть когда энергия поступает в систему. Эти графики показывают, что мгновенные значения энергетических характеристик даже в установившемся режиме достаточно сложно взаимосвязаны между собой – энергия, сообщаемая внешней силой, расходуется на изменение энергии системы (как кинетической, так и потенциальной), кинетическая энергия переходит в потенциальную и обратно, часть энергии теряется из-за наличия сопротивления. Более проста ситуация в случае точного резонанса, когда частота вынуждающей силы совпадает с собственной частотой колебаний системы. В этом случае механическая энергия системы остается постоянной, поэтому в любой момент времени мощность внешней силы в точности равна мощности потерь. Сдвиг фаз между вынуждающей силой и координатой точки равен ± π, что приводит к тому, что изменение скорости точки синфазно с изменением внешней силы. Следует отметить, что рассмотрение мгновенных энергетических характеристик представляет скорее академический интерес, с точки зрения практических применений более важно рассмотрение этих характеристик, усредненных по промежутку времени, значительно превышающему период колебаний. Тем более, это справедливо в тех случаях, когда частота колебаний настолько велика, что различить отдельное колебание не представляется возможным[7]. Проведем расчет усредненных энергетических характеристик в установившемся режиме вынужденных колебаний. Для начала получим одну важную математическую формулу, которую неоднократно будем использовать в дальнейшем. Пусть две функции изменяются по гармоническому закону с одной и той же частотой
Найдем среднее значение произведения этих функций, используя тригонометрическую формулу для произведения косинусов . Первое слагаемое (косинус разности фаз) не зависит от времени, второе - является переменной функцией времени, очевидно, что ее среднее значение равно нулю. Таким образом, мы получаем, что среднее произведение двух функций равно половине произведения амплитуд, умноженной на косинус сдвига фаз между ними
Частные случаи этой формулы, очевидны, и ранее уже применялись нами. Так при сдвиге фаз равном нулю среднее произведение равно половине произведения амплитуд - ранее мы показали, что среднее значение квадрата косинуса (и синуса) равно 0,5; при сдвиге фаз равном
Полученная формула имеет красивую геометрическую интерпретацию на языке векторного представления колебаний. Если гармонические функции представить в векторной форме (в виде вращающихся векторов), то их среднее произведение в соответствии с полученной формулой (8) равно половине скалярного произведения векторов, изображающих функции-сомножители (рис. 233). Обратимся еще раз к рис. 231, на котором построена векторная диаграмма, иллюстрирующая процесс вынужденных колебаний. С ее помощью легко получить те же энергетические характеристики, которые мы нашли аналитически. Убедитесь в этом самостоятельно. В заключение данного раздела получим явное выражение для средней мощности внешней силы (и равной ей мощности потерь) при вынужденных колебаниях. Эту величину разумно назвать средней мощностью поглощаемой системой. Проще всего это сделать, усредняя мгновенную мощность потерь (6)
при выводе этой функции использовано явное выражение для амплитуды вынужденных колебаний. Схематические графики зависимости поглощенной энергии от частоты вынуждающей силы при различных значениях параметра затухания показаны на рис. 234. Эти графики похожи на зависимости амплитуды от частоты вынуждающей силы (Рис. 227а), но следует помнить, что это, все-таки, разные функции.
Лекция 33
СОВМЕСТНАЯ РАБОТА МП И МЕТАЛЛОКОНСТУКЦИИ Сложность точного расчета совместного нагружения механизма и металлоконструкции моста (или другого каркаса) заключается в том, что такие системы имеют бесконечно большое число степеней свободы. Колебание таких систем описывается уравнениями в частных производных, решить которые можно только в простейших случаях, при этом решения представляют бесконечные ряды. Вместе с тем доказано, что для работы механизма достаточно, точные результаты дают схемы, в которых металлоконструкция представлена одномассовой парциальной системой. Простейшей схемой, описывающей совместное нагружение моста и механизма подъема, является трех-массовая схема с двумя звеньями.
Здесь
U – общее передаточное отношение механизма (с учетом кратности полиспаста)
m2 = Q+mnкг Q – масса груза, кг mn – масса подвески, кг, найденная по формуле
Gm=m3g – приведенный вес моста, Н Pдп=2Tcт.п·u - среднепусковой момент двигателя, Н·м
Учет податливости моста для нагрузок в канате при подъеме с веса и при подхвате имеет меньшее значение, чем при стопорении крюка. Уравнение движения для такой схемы при стопорении крюка выглядит следующим образом:
Где: – нагрузка привода при пуске, в первом приближении ее можно брать на уровне среднепусковой силы и принимать неизменной. Для нагрузок можно получить следующие двухчастотные функции:
Где:
Здесь u – скорость массы m1 перед стопорением, первому индексу у А, В и Наибольшие нагрузки в канатах и мосту с небольшим завышением могут быть посчитаны по следующим выражениям:
При движении крана мостового типа нагружение испытывают одновременно элементы трансмиссии механизма передвижения и мост, а груз при его гибкой подвеске на канатах начинает раскачиваться, как маятник. Эти особенности движения систем для описания нагрузок заставляют использовать четырехмассовую расчетную схему с тремя соединительными звеньями:
Здесь:
W – сила сопротивления движению Нагрузки звеньев в таких схемах как при разгоне, так и при торможении также обладают свойствами одночастотности упругих колебаний, что позволяет использовать упрощенный способ определения нагрузок с помощью двухмассовых схем, разных для различных звеньев (и в этих случаях массы всей системы приводятся по концам рассчитываемого звена). Установлено, что учет соударений в зубчатых муфтах и зубчатых передач трансмиссии механизма имеет значение только для первого звена (с коэффициентом жесткости с12), нагрузки во втором и третьем звеньях можно определять без учета соударений в передачах механизма. Учет соударений с концевыми упорами требует усложнения расчетной схемы, необходимо рассматривать «встречу» массы m2 c дополнительным звеном, имеющим коэффициент жесткости буферов. Как при центральном, так и при индивидуальном приводе механизма передвижения возможна ассиметрия кинематической схемы и по коэффициентам жесткости параллельно работающих трансмиссионных валов, и по зазорам в передачах, и по распределению масс. Установлено не благоприятное влияние любой асимметрии в кинематической схеме
Лекция 34 ДИНАМИКА МЕХАНИЗМОВ ПЕРЕДВИЖЕНИЯ
Лекция 35
НАГРУЗКИ В МЕТАЛЛОКОНСТРУКЦИИ ПРИ ПУСКЕ, ТОРМОЖЕНИИ, НАЕЗДЕ НА БУФЕРНОЕ УСТРОЙСТВО
Большинство динамических нагрузок металлических конструкций грузоподъемных машин возникает в результате силового воздействия металлоконструкций с установленными на ней механизмами. Для предварительного выяснения закономерности возникновения динамических нагрузок в металлоконструкциях предположим, что на металлоконструкцию действуют некоторые силы, зависящие только от времени. За расчетную динамическую схему металлоконструкции примем одномассовую систему с одной упругой связью. Рассмотрим сначала действие ограниченной, линейно возрастающей нагрузки Gгр(t).
Дифференциальное уравнение движения массы m при t < t1 имеет вид
Общее решение уравнения при нулевых начальных условиях т.е.
А скорость массы m (скорость деформации упругой связи)
Изменение деформации упругой связи при t1< t.
Между частотой р собственных колебаний системы и периодом Т собственных колебаний имеется зависимость в виде рТ = 2 Подставив выражение р в формулу * получим Рассматривая выражение **можно сделать вывод, что при
Начальные условия для решения этого уравнения находят путем подстановки в уравнения * и ** значения t = t1 Решая уравнение получаем:
Выражая р через Т имеем:
Максимальная деформация упругой связи
Изменения этого коэффициента в зависимости от отношения t1/T показано на рисунке далее штриховой линией. Как видно из рисунка, при мгновенном приложении нагрузки (t1 = 0) динамический коэффициент кд = 2, а при t1/T > 6, кп < 1.05 Динамическим влиянием нагрузки в этом случае можно пренебречь.
Для практических расчетов изменение динамического коэффициента принимается по кривой, показанной на рисунке сплошной линией. По изложенной методике можно ориентировочно оценить, например, динамическое воздействие на металлоконструкцию от веса поднимаемого с опоры груза, если за время развития нагрузки t1 принятьвремя натяжения подъемных канатов до отрыва груза от опоры.
Динамические нагрузки кранов при их пуске и торможении.
Лекция 36
ПРОБУКСОВКА И «ЮЗ» ПРИВОДНЫХ КОЛЕС
Лекция 37
ДИНАМИКА ПОВОРОТНЫХ КРАНОВ
Лекция 38 ПУСК И ТОРМОЖЕНИЕ МП-
Лекция 39
ДИНАМИЧЕСКИЕ НАГРУЗКИ (ИТОГ)
|
||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 1227; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.137 (0.012 с.) |

 , (1)
, (1)
 . (2)
. (2) описывает мгновенную мощность, развиваемой внешней вынуждающей силой. Величина
описывает мгновенную мощность, развиваемой внешней вынуждающей силой. Величина  является мощностью силы сопротивления и описывает потери механической энергии в единицу времени.
является мощностью силы сопротивления и описывает потери механической энергии в единицу времени. преобразовывается следующим образом
преобразовывается следующим образом , (3)
, (3) . (4)
. (4) . (5)
. (5) . (6)
. (6)
 . (7)
. (7) . (8)
. (8) среднее произведение равно нулю.
среднее произведение равно нулю.
 , (9)
, (9)

 – приведенная к грузу масса вращающихся частей механизма, кг,
– приведенная к грузу масса вращающихся частей механизма, кг, - момент инерции вращающихся масс, приведенная к валу двигателя, кг·
- момент инерции вращающихся масс, приведенная к валу двигателя, кг· 
 – КПД механизма
– КПД механизма – диаметр канатного барабана, м
– диаметр канатного барабана, м

 - приведенная к грузу пусковая сила двигателя,Н
- приведенная к грузу пусковая сила двигателя,Н – коэффициент жесткости каната,
– коэффициент жесткости каната, 
 – число ветвей каната в полиспасте
– число ветвей каната в полиспасте - Модуль упругости каната, МПа
- Модуль упругости каната, МПа - «металлическая» площадь поперечного сечения каната, м2
- «металлическая» площадь поперечного сечения каната, м2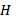 – длинна одной ветви каната (высота подъема), м
– длинна одной ветви каната (высота подъема), м - коэффициент жесткости моста, Н/м найденный по формуле
- коэффициент жесткости моста, Н/м найденный по формуле 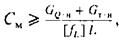
















 соответствует верхний знак перед дробью.
соответствует верхний знак перед дробью.

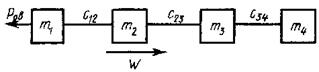
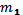 - масса вращающихся частей механизма передвижения
- масса вращающихся частей механизма передвижения - масса поступательно движущихся частей концевых элементов моста
- масса поступательно движущихся частей концевых элементов моста - масса поступательно движущихся пролетных частей моста + масса тележки
- масса поступательно движущихся пролетных частей моста + масса тележки - масса гипко подвешенного груза
- масса гипко подвешенного груза – коэффициент жесткости трансмиссии
– коэффициент жесткости трансмиссии - коэффициент жесткости моста в горизонтальном направлении
- коэффициент жесткости моста в горизонтальном направлении - коэффициент жесткости гибкой подвески груза
- коэффициент жесткости гибкой подвески груза








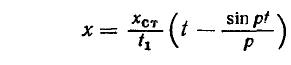 *
* **
**

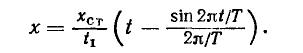


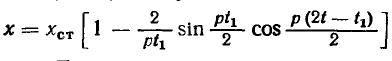
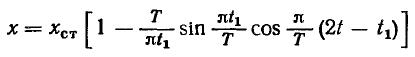 ***
***

























