Уравнение вынужденных колебаний и его решение.

Потери механической энергии в любой колебательной системе из-за наличия сил трения неизбежны, поэтому без «подкачки» энергии извне колебания будут затухающими. Существует несколько принципиально различных способов создания колебательных систем незатухающих колебаний. Остановимся более подробно на рассмотрении незатухающих колебаний под действием внешней периодической силы. Такие колебания называются вынужденными.

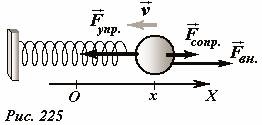
Помимо сил упругости и вязкого трения, на шарик(Рис. 225) действует внешняя вынуждающая периодическая сила, изменяющаяся по гармоническому закону

, (1)

частота, которой может отличаться от собственной частоты колебаний маятника ω ₀.

Природа этой сил в данном случае нам не существенна. Создать такую силу можно различными способами, например, сообщить шарику электрический заряд и поместить его во внешнее переменное электрическое поле.

Уравнение движения шарика в рассматриваемом случае имеет вид

. (2)

Разделим его на массу шарика и используем прежние обозначения параметров системы. В результате получим уравнение вынужденных колебаний:

. (3)

где - отношение амплитудного значения внешней вынуждающей силы к массе шарика.

Общее решение уравнения (3) достаточно громоздко и, конечно, зависит от начальных условий. Характер движения шарика, описываемого уравнением (3), понятен: под действием вынуждающей силы возникнуть колебания, амплитуда которых будет возрастать. Этот переходный режим достаточно сложен и зависит от начальных условий. По прошествии некоторого промежутка времени колебательный режим установится, их амплитуда перестанет изменяться. Именно установившийся режим колебаний, во многих случаях представляет основной интерес. Мы не будем рассматривать переход системы к установившемуся режиму, а сконцентрируем внимание на описании и изучении характеристик этого режима. При такой постановке задачи нет необходимости задавать начальные условия, так как интересующий нас установившийся режим не зависит от начальных условий, его характеристики полностью определяются самим уравнением.

.

По прошествии некоторого времени тело движется с постоянной установившейся скоростью , которая не зависит от начальных условий, и полностью определяется уравнением движения. Начальные условия определяют режим, переходный к установившемуся движению.

На основании здравого смысла разумно предположить, что в установившемся режиме колебаний шарик будет колебаться с частотой внешней вынуждающей силы. Поэтому решение уравнения (3) следует искать в гармонической функции с частотой вынуждающей силы.

Для начала решим уравнение (3), пренебрегая силой сопротивления

. (4)

Попробуемнайти его решение в виде гармонической функции

. (5)

Для этого вычислим зависимости скорости и ускорения тела от времени, как производные от закона движения

,

и подставим их значения в уравнение (4)

.

Теперь можно сократить на cos ωt. Следовательно, это выражение обращается в верное тождество в любой момент времени, при выполнении условия

. (6)

Таким образом, наше предположение о решении уравнения (4) в виде (5) оправдалось: установившийся режим колебаний описывается функцией

. (7)

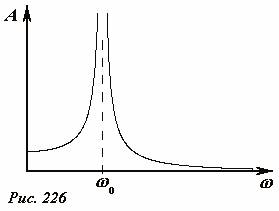
Отметим, что коэффициент A согласно полученному выражению (6) может как положительным (при ω ₀< ω), так и отрицательным (при ω ₀> ω). Изменение знака соответствует изменению фазы колебаний на π (причина такого изменение будет выяснена чуть позже), поэтому амплитудой колебаний является модуль этого коэффициента A. Амплитуда установившихся колебаний, как и следовало ожидать, пропорциональна величине вынуждающей силы. Кроме того, эта амплитуда сложным образом зависит от частоты вынуждающей силы. Схематический график этой зависимости показан на Рис. 226.

Как следует из формулы (6) и хорошо видно на графике, при приближении частоты вынуждающей силы к собственной частоте системы амплитуда резко возрастает. Причина такого возрастания амплитуды понятна: вынуждающая сила «во время» подталкивает шарик, при полном совпадении частот установившейся режим отсутствует – амплитуда возрастает до бесконечности. Конечно, на практике такого бесконечного возрастания наблюдать невозможно: во-первых, это может привести к разрушению самой колебательной системы, во-вторых, при больших амплитудах колебаний нельзя пренебрегать силами сопротивления среды.