
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Динамика подъема груза с опоры механизмом, установленным на жестком основании.Содержание книги
Поиск на нашем сайте
Этот расчетный случай является сложным и мало-определенным, поскольку на динамические нагрузки при подъеме груза с опоры оказывают влияние такие дополнительные факторы, как тип контроллера механизма подъема и способ управления двигателем (последовательность операций управления), вид основания (опоры), с которого поднимается груз, конфигурация (форма) груза, его монолитность и т. п., качество строповки груза и зависимость жесткости подвески груза от натяжения канатов. После зачаливания груза перед его подъемом в канатах всегда есть некоторая слабина, которая выбирается кратковременным включением двигателя либо постоянным включением двигателя для работы на подъем груза. Поскольку нагрузка на двигатель при выборе слабины каната очень мала, его разгон до установившейся скорости происходит очень быстро. Поэтому при выборе очень незначительной слабины каната двигатель практически имеет частоту вращения, как при холостом ходе. Такой подъем груза с опоры, при котором усилие в канатах начинает возрастать при частоте вращения холостого хода двигателя, принято называть режимом подъема груза «с подхватом». Подъем груза с опоры, при котором включение двигателя происходит при натяжении каната, меньшем усилия от массы поднимаемого груза, принято называть режимом подъема груза «с упругим подхватом». Подъем груза с подхватом может происходить при работе двигателя на естественной и искусственной механических характеристиках. Подъем груза на естественной характеристике более вероятен при управлении двигателем с помощью силового (кулачкового) контроллера, а подъем груза на искусственной характеристике более вероятен при управлении двигателем с помощью магнитного контроллера. Вид опоры, с которой поднимается груз, влияет на динамику процесса подъема следующим образом. Если опора весьма жесткая (бетонный пол), то в момент отрыва груза от основания его скорость близка к нулю. Если опора обладает некоторой ощутимой податливостью (деревянный пол или деревянные брусья на бетонном полу), то в момент отрыва груза от основания его скорость сильно отличается от нулевой, что в конечном итоге приводит к уменьшению максимальных динамических нагрузок. При подъеме груза возможен одновременный отрыв всех опорных точек груза от основания (опоры) либо последовательный отрыв этих точек. Одновременный отрыв возможен при подъеме монолитного жесткого груза при строгом соблюдении центральнойстроповки. Если груз состоит из отдельных элементов (связка сортового проката), обладает малой жесткостью (рулон листового проката) и имеет нецентральнуюстроповку, отрыв груза происходит путем последовательного уменьшения числа точек контакта с опорой. При анализе влияния дополнительных факторов на динамические нагрузки экспериментально и методом сравнительных расчетов было установлено, что максимальные динамические нагрузки возникают при подъеме жесткого монолитного груза с жесткого основания с подхватом при центральной строповке груза, при работе двигателя на самой жесткой механической характеристике. Подъем груза при других условиях приводит к снижению динамических нагрузок. Учитывая этот фактор, максимальные расчетные динамические нагрузки в элементах механизма подъема можно определять по зависимости
где
Максимальную динамическую нагрузку Возникновение динамических усилий в канатах при подъеме груза с опоры происходит в две стадии. В первой, доотрывной стадии происходит нарастание усилия в канатах до величины при неподвижной массе Экспериментально установлено, что коэффициент жесткости подъемных канатов в основном зависит от натяжения подъемных канатов (плавная кривая на рис. 2). Динамический расчет с учетом непостоянного коэффициента c может быть выполнен только численным методом с применением ЭВМ, причем для упрощения решения плавную кривую удобнее заменить ступенчатой кривой, как это показано на рис. 2. С некоторой погрешностью, направленной на увеличение максимума нагрузок, динамический расчет может быть выполнен аналитически в предположении постоянства коэффициента Доотрывная стадия. В этой стадии за начальные принимают следующие показатели: начальную скорость движения
где Так как к началу возрастания усилия в подвеске груза двигатель имеет максимальную частоту вращения, близкую к частоте вращения при холостом ходе, по мере увеличения натяжения в канатах частота вращения двигателя и, следовательно, скорость массы тх несколько уменьшаются, а движущее усилие увеличивается, причем это усилие в доотрывной стадии изменяется в больших пределах. Поэтому движущее усилие необходимо принимать в зависимости от скорости массы Принимая движущее усилие по уравнению
получаем дифференциальное уравнение движения массы
где Решая это уравнение, имеем
где Подъем груза с опоры с подхватом, если двигатель при выборе слабины каната имеет максимальную частоту вращения, происходит при работе приводного двигателя на какой-то одной механической характеристике. Если двигатель работает на естественной характеристике, то параметр Подставляя в уравнение (3) значение, получаем уравнение для определения времени
Это трансцендентное уравнение следует решать на ЭВМ по стандартной программе. Дифференцируя уравнение (3) по времени и подставляя значение
Послеотрывная стадия. Для расчета послеотрывной стадии сначала рассмотрим систему с двумя поступательно-перемещающимися массами
При движении системы усилие в упругом звене
Дифференциальное уравнение движения первой массы имеет вид
Уравнение движения второй массы
Для определения усилия в упругом звене, пропорционального разности перемещений
Дифференцируем уравнение (4) дважды по времени, имеем
Подставляя это выражение и (4) в уравнение (7), получаем
где
За начало отсчета времени и перемещения принимается начало послеотрывной стадии. В этот период движущее усилие мало отличается от веса груза. Поэтому, принимая приближенно, дифференциальное уравнение для определения усилия в упругом элементе в послеотрывной стадии имеет вид
где
Уравнение (9) получено тем же методом, что и уравнение (8). Поскольку (здесь
Решение уравнения (9) при этих начальных условиях имеет вид Отсюда следует, что значение усилия в упругом элементе после отрыва груза от опоры колеблится около значения с амплитудой и круговой частотой Максимальное усилие в послеотрывной стадии
Из этого выражения следует, что динамическое максимальное усилие в упругом элементе тем больше, чем больше его жесткость с и скорость подхвата груза. Во многих кранах кинетическая энергия вращающихся частей механизма подъема во много раз больше кинетической энергии поднимаемого груза номинальной массы, т. е.
Действительные значения максимального усилия несколько меньше получаемых по этому уравнению значений. Однако простота и предельная ясность физического смысла этого выражения привели к очень широкому его использованию в практических предварительных расчетах.
Лекция 31
ПОДЪЕМ «С ВЕСА» И С ОПОРЫ РАБОТА ПОДЪЕМНОГО МЕХАНИЗМА С ПОДВЕШЕННЫМ ГРУЗОМ
Динамические явления в крановых механизмах и металлоконструкциях можно изучать с помощью упрощенных схем с ограниченным числом степеней свободы. Эти приведенные схемы интерпретируют работу машины как движение нескольких абсолютно жестких точечных масс, соединенных упругими невесомыми связями, под воздействием внешних нагрузок. Работа подъемного механизма с подвешенным на крюке грузом отличается тем, сто перед началом движения нет слабины (свободного напуска) в канатах, все упругие элементы механизма уже подвергнуты действию веса груза, зазоры в зацеплениях выбраны и все массы упругой системы начинают движение одновременно. При нормальной эксплуатации этот режим нагружения повторяется наиболее часто и, как правило, почти не зависит от приемов работы крановщика. Особенностями расчетных схем, описывающих работу подъемного механизма, является, во-первых, то, что здесь канаты представляют собой упругую связь одностороннего действия (работают только на растяжение), а, во-вторых, статическая нагрузка от веса груза независимо от направления движения всей системы направлена только вниз, в сторону опускания груза.
ДВУХМАССОВЫЕ РАСЧЕТНЫЕ СХЕМЫ
Чем большее число масс будет введено в расчетную схему, тем точнее она отражает происходящие явления, но и тем сложнее будут уравнения движения и в особенности решения этих уравнении. Наиболее простой является двухмассовая односвязная схема. При сравнительно простых математических выкладках она дает точность первого приближения, часто удовлетворяющую требованиям практики. При составлении двухмассовой схемы учитывается упругость того элемента, жесткость которого является минимальной; массы, расположенные по обе стороны от этого элемента, приводятся к двум массам. Например, в механизме подъема при определении усилий в канатах учитывается упругость подвески груза; одной из масс расчетной схемы является масса груза, а другой — приведенная к перемещению груза масса вращающихся частей механизма. Для определения усилий, передаваемых первичным валом редуктора механизма поворота крана, одной из масс расчетной схемы является масса ротора двигателя и муфты, а другой — приведенная масса остальных вращающихся частей механизма. Рассмотрим случай подъема вверх «с веса».
Выражение для упругой нагрузки: F=Q+C(x1-x2); Здесь х1 и х2 – пути перемещения соответствующих масс схемы. Дифференцируем дважды последнее уравнение, вторые производные
Переносим неизвестную силу влево и записываем полученное уравнение
Относительно искомой нагрузки F получено неоднородное линейное дифференциальное уравнение второго порядка с постоянными коэффициентами. Общим решением этого уравнения является сумма гармонических функций и частного решения: F=Acosωt + Bsinωt + D, Где квадрат круговой частоты собственных колебаний равен множителю при искомой функции F в стандартном уравнении
Необходимо отметить независимость круговой частоты и периода собственных колебаний от внешних нагрузок. Это видно из следующих формул:
Частота и период определяются только коэффициентом жесткости упругой связи и величинами масс. Произведение квадрата частоты и частного решения равно неоднородному члену стандартного уравнения
Откуда
Таким образом, частное решение представляет собой сумму статической нагрузки Q и так называемой свободной силы инерции В общем решении для нагрузки присутствуют еще гармонические колебания, амплитуды которых А и В следует определить из начальных условий. При t=0 x10=x20= 0;
Окончательно получаем
Так как при разгоне всегда соблюдается неравенство P>Q, то наибольшее значение нагрузки упругой связи наступает в момент, когда t=
Наименьшая величина нагрузки упругой связи будет при t=0 – Fmin=Q При разгоне вверх наибольшая нагрузка упругой связи получается в виде суммы силы статического сопротивления движению и удвоенной силы инерции массы m2, являющейся массой ведомой. Если бы не учитывалась упругость связи, то динамическая добавка была бы в два раза меньше. Следовательно учет упругости кинематических элементов механизма при разгоне с веса удваивает инерционную добавку. Подставляя полученное выражение нагрузки упругой связи в исходные дифференциальные уравнения движения, получаем формулы для ускорений масс:
Интегрируя эти выражения при указанных выше начальных условиях, получаем формулы для скоростей:
Как и следовало ожидать, скорости движения масс меняются по закону равноускоренного движения с гармоническими колебаниями, величина которых зависит от ускорения системы (ускорения центра инерции масс)
и частоты собственных упругих колебаний. Амплитуды гармонических возмущений относятся друг к другу обратно пропорционально массам. Амплитуда гармонического возмущения у большей массы – меньшая, и наоборот. Приведенные формулы свидетельствуют о независимости предельных нагрузок от коэффициента жесткости упругой связи. Они определяются действием статической нагрузки предварительного нагружения, с одной стороны, и удвоенной силы инерции свободной массы с другой.
ПОДЪЕМ ГРУЗА «С ПОДХВАТОМ» Соударения в кинематических парах подъемного механизма происходят в системах с зазорами, а также в механизмах с упругими связями одностороннего действия, когда возможно силовое размыкание и изменение кинематической структуры. Соударения в системе полагают достаточно мягкими или неупругими. При этом учитывают только деформации основных упругих элементов системы – канатов, валов, пружин и др. Местные деформации соударяющихся тел в расчет не принимаются, так как время деформирования контактных зон очень мало по сравнению с периодами собственных колебаний упругой системы. «ПОДХВАТ» В ДВУХМАССОВОЙ СИСТЕМЕ
Наиболее просто этот режим можно изучить с помощью двухмассовой схемы с постоянными параметрами в интерпретации поступательного движения. Считаем, что груз поднимается с абсолютно жесткой опоры в режиме неустановившегося движения, а зазор в кинематических парах механизма приведен к безмассовой упругой связи с коэффициентом жесткости C. В ходе первого этапа первая масса m1 (рис. 10,а) двигается равноускоренно под действием постоянной по величине среднепусковой силы Р, выбирая зазор Δ. Длительность первого этапа
Скорость первой массы к концу первого этапа
На втором этапе упругой связи возникает нагрузка F2 (рис.10,б), и пока она меньше нагрузки статического сопротивления Q(веса груза), вторая масса m2 покоится, в движении находится только первая масса. Длительность второго этапа определяется временем возрастания нагрузки упругой связи от нуля до веса груза Q.
Третий этап характерен совместным движением обеих масс (рис.10,в) В данном случае частота собственных колебаний ω3 и амплитуда косинусоидальной составляющей А3 ничем не отличаются от таких же величин при подъеме «с веса». Особенность рассматриваемого этопа – в появлении зависящей от начальной скорости синусоидальной составляющей, амплитуда которой равна силе разрядки от действия ведущей массы:
Появление синусоидальной составляющей не только увеличивает наибольшую динамическую нагрузку упругого звена, но может привести к качественным изменениям в характере движения упругой связи. ДИНАМИКА ПОДЪЕМА ГРУЗА С ОПОРЫ МЕХАНИЗМОМ, УСТАНОВЛЕННЫМ НА ЖЕСТКОМ ОСНОВАНИИ Этот расчетный случай является более сложным и менее определенным, чем предыдущий, поскольку на динамические нагрузки при подъеме груза с опоры оказывают влияние такие дополнительные факторы, как тип контроллера механизма подъема и способ управления двигателем (последовательность операций управления), вид основания (опоры), с которого поднимается груз, конфигурация (форма) груза, его монолитность и т. п., качество строповки груза и зависимость жесткости подвески груза от натяжения канатов. После зачаливания груза перед его подъемом в канатах всегда есть некоторая слабина, которая выбирается кратковременным включением двигателя либо постоянным включением двигателя для работы на подъем груза. Поскольку нагрузка на двигатель при выборе слабины каната очень мала, его разгон до установившейся скорости происходит очень быстро. Поэтому при выборе очень незначительной слабины каната двигатель практически имеет частоту вращения, как при холостом ходе. Такой подъем груза с опоры, при котором усилие в канатах начинает возрастать при частоте вращения холостого хода двигателя, принято называть режимом подъема груза «с подхватом». Подъем груза с опоры, при котором включение двигателя происходит при натяжении каната, меньшем усилия от массы поднимаемого груза, принято называть режимом подъема груза «с упругим подхватом». Подъем груза с подхватом может происходить при работе двигателя на естественной и искусственной механических характеристиках. Подъем груза на естественной характеристике более вероятен при управлении двигателем с помощью силового (кулачкового) контроллера, а подъем груза на искусственной характеристике более вероятен при управлении двигателем с помощью магнитного контроллера. Вид опоры, с которой поднимается груз, влияет на динамику процесса подъема следующим образом. Если опора весьма жесткая (бетонный пол), то в момент отрыва груза от основания его скорость близка к нулю. Если опора обладает некоторой ощутимой податливостью (деревянный пол или деревянные брусья на бетонном полу), то в момент отрыва груза от основания его скорость сильно отличается от нулевой, что в конечном итоге приводит к уменьшению максимальных динамических нагрузок. При подъеме груза возможен одновременный отрыв всех опорных точек груза от основания (опоры) либо последовательный отрыв этих точек. Одновременный отрыв возможен при подъеме монолитного жесткого груза при строгом соблюдении центральной строповки. Если груз состоит из отдельных элементов (связка сортового проката), обладает малой жесткостью (рулон листового проката) и имеет нецентральную строповку, отрыв груза происходит путем последовательного уменьшения числа точек контакта с опорой.
где Sn.max— максимально возможная для данного механизма подъема динамическая нагрузка; k1 — коэффициент, учитывающий податливость основания; k2— коэффициент, учитывающий немонолитность груза. Максимальную динамическую нагрузку Smax механизма подъема, установленного на жестком основании, можно определить, используя расчетную схему на рис. 12.11. Механизм подъема можно считать установленным на жестком основании тогда, когда при расчете можно пренебречь энергией упругих колебаний крановой металлоконструкции по сравнению с энергией упругих колебаний механизма подъема. К таким случаям относится подъем груза при расположении грузовой тележки крана мостового типа вблизи опоры и в других случаях. Возникновение динамических усилий в канатах при подъеме груза с опоры происходит в две стадии. В первой, доотрывной стадии происходит нарастание усилия в канатах до величины Grp при неподвижной массе m1 после чего начинается вторая, послеотрывная стадия, которая начинается с движения массы m2 (груза), оторванной от опоры. Характерной особенностью расчетной схемы на рис. 12.11 является непостоянный коэффициент жесткости подъемных канатов с в доотрывной стадии, т. е. в области малых натяжений канатов. Экспериментально установлено, что коэффициент жесткости подъемных канатов в основном зависит от натяжения подъемных канатов (плавная кривая на рис. 12.12). Динамический расчет с учетом непостоянного коэффициента с может быть выполнен только численным методом с применением ЭВМ, причем для упрощения решения плавную кривую удобнее заменить ступенчатой кривой, как это показано на рис. 12.12. С некоторой погрешностью, направленной на увеличение максимума нагрузок, динамический расчет может быть выполнен аналитически в предположении постоянства коэффициента с = сн следующим методом. Доотрывная стадия. Дифференциальное уравнение движения массы m1 имеет вид
Так как к началу возрастания усилия в подвеске груза двигатель имеет максимальную частоту вращения, близкую к частоте вращения при холостом ходе, по мере увеличения натяжения в канатах частота вращения двигателя и, следовательно, скорость массы m1 несколько уменьшаются, а движущее усилие увеличивается, причем это усилие в доотрывной стадии изменяется в больших пределах. Поэтому движущее усилие необходимо принимать в зависимости от скорости массы m1, а не считать его постоянным. Принимая движущее усилие по уравнению (12.14), получаем дифференциальное уравнение движения массы m1 в следующем виде:
Решая это уравнение, имеем
После того как перемещение хх достигает такого значения, при котором усилие в упругом элементе будет равно весу груза Grp, заканчивается доотрывная стадия.
Лекция 32
ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ И РЕЗОНАНСЫ Механическими колебаниями (или просто колебаниями) называется такое движение механической системы при котором обобщенные координаты и их производные изменяются во времени периодически возрастая или убывая. Различают следующие виды механических колебаний:
В данной работе мы рассмотрим один из видов механических колебаний – вынужденные колебания и резонанс.
|
|||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 1164; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.223.159.143 (0.013 с.) |

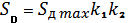
 — максимально возможная для данного механизма подъема динамическая нагрузка;
— максимально возможная для данного механизма подъема динамическая нагрузка;  — коэффициент, учитывающий податливость основания;
— коэффициент, учитывающий податливость основания;  — коэффициент, учитывающий немонолитность груза.
— коэффициент, учитывающий немонолитность груза.


 после чего начинается вторая, послеотрывная стадия, которая начинается с движения массы
после чего начинается вторая, послеотрывная стадия, которая начинается с движения массы  следующим методом.
следующим методом. массы
массы  , перемещение
, перемещение  , усилие
, усилие  . Поскольку в доотрывной стадии
. Поскольку в доотрывной стадии  и
и  , дифференциальное уравнение движения массы
, дифференциальное уравнение движения массы 
 — собственная частота (рад/с) колебаний массы
— собственная частота (рад/с) колебаний массы  ; P — движущее усилие.
; P — движущее усилие.

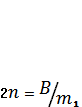

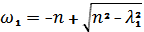 ;
;  .
. больше
больше 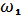 и
и  вещественны. Если двигатель работает на искусственной характеристике, то значения
вещественны. Если двигатель работает на искусственной характеристике, то значения  достигает такого значения, при котором усилие в упругом элементе будет равно весу груза, заканчивается доотрывная стадия.
достигает такого значения, при котором усилие в упругом элементе будет равно весу груза, заканчивается доотрывная стадия. отрыва груза от опоры
отрыва груза от опоры , определим скорость массы
, определим скорость массы 
 Например, это может быть расчетная схема для определения суммарных усилий во всех канатах подвески груза механизма подъема. К массе
Например, это может быть расчетная схема для определения суммарных усилий во всех канатах подвески груза механизма подъема. К массе  , к массе
, к массе 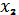 . Движение начинается после растормаживания массы
. Движение начинается после растормаживания массы 
 . Для этого умножая все члены уравнения (5) на
. Для этого умножая все члены уравнения (5) на 

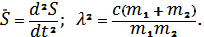
 – усилие упругого элемента в послеотрывной стадии;
– усилие упругого элемента в послеотрывной стадии;  –частота колебаний относительно друг друга, рад/с:
–частота колебаний относительно друг друга, рад/с:
 ) начальные условия будут следующие:
) начальные условия будут следующие:

 . Например, в мостовых кранах общего назначения грузоподъемностью 5—50 т
. Например, в мостовых кранах общего назначения грузоподъемностью 5—50 т  . Для таких механизмов при работе двигателя на естественной характеристике приближенное усилие в упругом элементе при подъеме груза с опоры с подхватом определяют следующим образом. Считая, что масса
. Для таких механизмов при работе двигателя на естественной характеристике приближенное усилие в упругом элементе при подъеме груза с опоры с подхватом определяют следующим образом. Считая, что масса  Растягивающую нагрузку упругой связи F прикладываем к обеим массам, после чего можем рассматривать уравнение движения каждой массы в отдельности:
Растягивающую нагрузку упругой связи F прикладываем к обеим массам, после чего можем рассматривать уравнение движения каждой массы в отдельности:
 и
и  берем по первым двум уравнениям:
берем по первым двум уравнениям: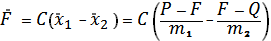





 . Эта сумма представляет собой величину нагрузки, которую испытывает абсолютно жесткая связь между массами.
. Эта сумма представляет собой величину нагрузки, которую испытывает абсолютно жесткая связь между массами.

 +
+  и cosωt= -1.Таким образом
и cosωt= -1.Таким образом



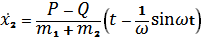
 Такой режим характеризуется тем, что при отрыве груза от опоры ведущие части механизма уже имеют определенную скорость и поэтому начальные скорости движения вращающихся масс не являются нулевыми.
Такой режим характеризуется тем, что при отрыве груза от опоры ведущие части механизма уже имеют определенную скорость и поэтому начальные скорости движения вращающихся масс не являются нулевыми.



 При анализе влияния дополнительных факторов на динамические нагрузки экспериментально и методом сравнительных расчетов было установлено, что максимальные динамические нагрузки возникают при подъеме жесткого монолитного груза с жесткого основания с подхватом при центральной строповке груза, при работе двигателя на самой жесткой механической характеристике. Подъем груза при других условиях приводит к снижению динамических нагрузок. Учитывая этот фактор, максимальные расчетные динамические нагрузки в элементах механизма подъема можно определять по зависимости
При анализе влияния дополнительных факторов на динамические нагрузки экспериментально и методом сравнительных расчетов было установлено, что максимальные динамические нагрузки возникают при подъеме жесткого монолитного груза с жесткого основания с подхватом при центральной строповке груза, при работе двигателя на самой жесткой механической характеристике. Подъем груза при других условиях приводит к снижению динамических нагрузок. Учитывая этот фактор, максимальные расчетные динамические нагрузки в элементах механизма подъема можно определять по зависимости






