
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Раздел 9. Динамические нагрузки гпмСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
Составление расчетных схем
Как правило, полагается, что разгон до скорости установившегося движения происходит равноускоренно, то есть
где В реальной машине отдельные звенья связаны между собой упругими связями (валами, канатами), что приводит в переходных режимах движения к появлению в связях динамических нагрузок упруго-колебательного характера. Амплитуды этих нагрузок могут быть значительными, особенно в областях резонансных частот. Только при наличии данных о характере и величине этих нагрузок можно обоснованно проводить расчеты несущей способности, прочности и долговечности деталей грузоподъемных машин, то есть корректно решать вторую и третью основные задачи, указанные во введении. На рис. 2а приведена исходная схема механизма подъема крана.
Расчетная схема заменяет реальный механизм и представляется рядом точечных масс (груз, шкив, барабан, зубчатые колеса), соединенных невесомыми упругими связями (валы, канаты). Параметры нового заменяющего механизма (массы, жесткости связей, приложенные силы и моменты) и называют приведенными. Расчетные параметры можно приводить в любое заранее выбранное место механизма, на любой упругий элемент, чем и объясняется многообразие заменяющих механизмов и расчетных схем. Естественно, такая замена должна быть обоснованной, а расчетная схема эквивалентна реальной, что выполняется при соблюдении ряда условий.
1. Приведение масс проводят на основе равенства кинетической энергии тела в основном и в заменяющем механизме. Например, в схеме 2в заменяющий механизм представлен в виде двигателя и тяжелого маховика с приведенным моментом Так же приводится к первому валу момент инерции барабана. В основном механизме При формировании схемы на рис.2г в массу m7входят приведенные к грузу массы всех вращающихся деталей. Масса груза m8 и жесткость С78 канатной подвески остаются неизменными. Приведем, для примера, к грузу момент инерции барабана I7 . Кинетическая энергия барабана в основном механизме
В первом приближении расчетная схема механизма представляется рядом точечных масс, соединенных невесомыми упругими связями.
Лекция 30
МП НА ЖЕСТКОМ ОСНОВАНИИ Рис. 231 Геометрическая сумма этих трех векторов (найти которую в данном случае можно элементарно) должна быть равна вектору, изображающему вынуждающую силу. Так как в исходном уравнении именно эта функция имеет нулевую фазу, то отсчет угла сдвига фаз должен проводится именно от этого вектора. Так на приведенном рисунке этот угол отрицателен, так поворот от вектора, изображающего вынуждающую силу, к вектору, изображающему зависимость x (t), осуществляется в отрицательном направлении («по часовой стрелке»).
Используя построенную диаграмму легко записать уравнение, связывающее амплитуду колебаний и амплитуду вынуждающей силы (на основании теоремы Пифагора):
из которого следует выражение для амплитуды вынужденных колебаний
естественно, совпадающее с полученным ранее аналитическим методом. Векторная диаграмма дает такое же выражение и для сдвига фаз
Таким образом, метод векторных диаграмм позволяет получать точные формулы гораздо быстрее, чем традиционный аналитический метод, основанный на громоздких преобразованиях тригонометрических формул. Раздел 9. Динамические нагрузки ГПМ
Лекция 29
ПРИВЕДЕНИЕ НАГРУЗОК, МАСС, ЖЕСТКОСТЕЙ
Введение. В переходный период российской экономики перед специалистами по расчетам ГПМ четко обозначились две основные проблемы: 1) проектирование новых конкурентоспособных машин и 2) расчет остаточного ресурса механизмов и машин, отработавших нормативный срок. В том и другом случае нужны все более точные решения триединой задачи: -определение характера и величины действующих нагрузок; -определение НДС элементов конструкций; -прогнозирование прочностных и ресурсных характеристик ГПМ. В плане решения первой задачи в пособии рассмотрены вопросы определения динамических нагрузок в деталях и узлах ГПМ с использованием теории колебаний. Приводятся числовые примеры, иллюстрирующие расчет нагрузок в переходные режимы нагружения. Отмечается, что только с учетом динамического характера нагрузок в упругих элементах машины можно обоснованно проводить расчеты несущей способности, прочности и долговечности. Отмечается, также, что практическое использование динамических расчетов связано не только с уточнением решений двух других задач. В ряде случаев вскрываются причины поломок и аварий механизмов, а также выявляются ненадежные узлы и резервы повышения грузоподъемности машин. Рассмотренные задачи динамики могут быть использованы и далее развиты при выполнении учебно-исследовательских работ, при курсовом и дипломном проектировании студентами специальности 190205 – «подъемно транспортные, строительные, дорожные машины и оборудование ».
а) Приведение внешних нагрузок.
Если приведение производится к более быстроходному звену, то надо разделить на
где
где
Практически работа сил трения А тр считается постоянной и учитывается с помощью КПД.
Кинетическая энергия приведенной системы при приведении к первому валу (валу двигателя)
Тогда с учетом потерь от сил трения (с учетом КПД)
где Iпр - приведенный момент инерции при пуске; w1 - угловая скорость вала двигателя; I1...In - моменты инерции масс, вращающихся со скоростями w1...wn; m1...mk - массы элементов, движущихся поступательно со скоростями V1...Vk;
где
можно записать выражение для приведенного момента инерции механизма (при пуске):
При торможении формула получается аналогично и отличается только перемещением КПД из знаменателя выражений в числитель.
влияние этих членов невелико (так как в знаменателе
а для торможения
В справочниках часто приводятся не моменты инерции, а маховые моменты, между которыми следующая связь:
где
· при торможении
где
где Р - сила, вызывающая линейную деформацию y; М - момент, вызывающий угловую деформацию На валу 2 в силовом режиме действует момент М, который при жесткости вала с вызывает его деформацию
Приведем крутящий момент к валу 1.
Приведем деформацию вала 2 к валу 1
C учетом уравнений (*) и (**) определим приведенную к валу 2 жесткость вала 1
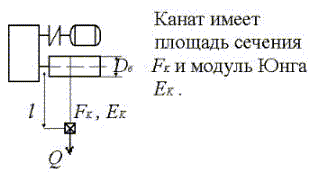
Жесткости приводятся от одного вала к другому аналогично моментам инерции и массам. Приведем линейную жесткость одинарного полиспаста к крутильной (к валу барабана).
Деформация каната (линейная)
где с - жесткость каната.
Действие веса груза Q на канат эквивалентно действию на окружность барабана крутящего момента MQ
Жесткость каната, приведенная к оси барабана
Нетрудно показать, что жесткость каната, приведенная к валу двигателя, определяется по формуле
где Составление расчетных схем
Как правило, полагается, что разгон до скорости установившегося движения происходит равноускоренно, то есть
где В реальной машине отдельные звенья связаны между собой упругими связями (валами, канатами), что приводит в переходных режимах движения к появлению в связях динамических нагрузок упруго-колебательного характера. Амплитуды этих нагрузок могут быть значительными, особенно в областях резонансных частот. Только при наличии данных о характере и величине этих нагрузок можно обоснованно проводить расчеты несущей способности, прочности и долговечности деталей грузоподъемных машин, то есть корректно решать вторую и третью основные задачи, указанные во введении. На рис. 2а приведена исходная схема механизма подъема крана.
Расчетная схема заменяет реальный механизм и представляется рядом точечных масс (груз, шкив, барабан, зубчатые колеса), соединенных невесомыми упругими связями (валы, канаты). Параметры нового заменяющего механизма (массы, жесткости связей, приложенные силы и моменты) и называют приведенными. Расчетные параметры можно приводить в любое заранее выбранное место механизма, на любой упругий элемент, чем и объясняется многообразие заменяющих механизмов и расчетных схем. Естественно, такая замена должна быть обоснованной, а расчетная схема эквивалентна реальной, что выполняется при соблюдении ряда условий. 1. Приведение масс проводят на основе равенства кинетической энергии тела в основном и в заменяющем механизме. Например, в схеме 2в заменяющий механизм представлен в виде двигателя и тяжелого маховика с приведенным моментом Так же приводится к первому валу момент инерции барабана. В основном механизме При формировании схемы на рис.2г в массу m7входят приведенные к грузу массы всех вращающихся деталей. Масса груза m8 и жесткость С78 канатной подвески остаются неизменными. Приведем, для примера, к грузу момент инерции барабана I7 . Кинетическая энергия барабана в основном механизме
В первом приближении расчетная схема механизма представляется рядом точечных масс, соединенных невесомыми упругими связями.
Лекция 30
МП НА ЖЕСТКОМ ОСНОВАНИИ
|
||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 930; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.220.130.220 (0.013 с.) |

 В теоретической механике рассматриваются механические системы абсолютно твердых тел, соединенных идеальными связями. Такие модели реальной машины используются в проектных расчетах для определения мощности двигателя, тормозного момента, сил сопротивления качению и др. Динамические нагрузки пуско-тормозных режимов оцениваются добавлением, в соответствии с принципом Даламбера, сил и моментов инерции. При поступательном движении элемента системы (груза, тележки) к действующим на него силам добавляют силу инерции
В теоретической механике рассматриваются механические системы абсолютно твердых тел, соединенных идеальными связями. Такие модели реальной машины используются в проектных расчетах для определения мощности двигателя, тормозного момента, сил сопротивления качению и др. Динамические нагрузки пуско-тормозных режимов оцениваются добавлением, в соответствии с принципом Даламбера, сил и моментов инерции. При поступательном движении элемента системы (груза, тележки) к действующим на него силам добавляют силу инерции  , а при вращательном (барабан, блок) момент сил инерции
, а при вращательном (барабан, блок) момент сил инерции  . Здесь m, I- масса и момент инерции тела,
. Здесь m, I- масса и момент инерции тела,  - линейное и угловое ускорение (рис.1). Знак минус означает, что векторы направлены противоположно.
- линейное и угловое ускорение (рис.1). Знак минус означает, что векторы направлены противоположно. ,
, - время разгона. Те же предположения принимаются и при исследовании режима торможения.
- время разгона. Те же предположения принимаются и при исследовании режима торможения.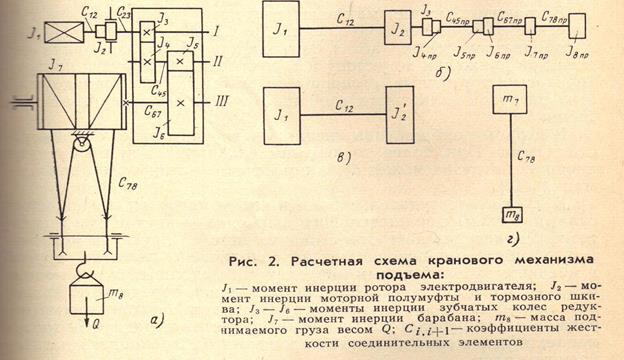 На рис. 2б,2в,2г приведены различные варианты расчетных схем, к которым можно «привести» исходную схему механизма в зависимости от решаемой задачи. Если требуется найти динамические нагрузки во всех связях, то выбирается схема 2б, если интересуют нагрузки только на валу двигателя или в канатах, то принимается схема 2в или 2г, соответственно. Рассмотрим подробнее вопрос о приведенных величинах в расчетных схемах механизма.
На рис. 2б,2в,2г приведены различные варианты расчетных схем, к которым можно «привести» исходную схему механизма в зависимости от решаемой задачи. Если требуется найти динамические нагрузки во всех связях, то выбирается схема 2б, если интересуют нагрузки только на валу двигателя или в канатах, то принимается схема 2в или 2г, соответственно. Рассмотрим подробнее вопрос о приведенных величинах в расчетных схемах механизма. , в который входит приведенный к первому валу момент от веса груза. Кинетическая энергия груза в реальном механизме
, в который входит приведенный к первому валу момент от веса груза. Кинетическая энергия груза в реальном механизме  , а в заменяющем
, а в заменяющем  . Далее надо выразить скорость подъема груза через угловую скорость вала двигателя (или наоборот)
. Далее надо выразить скорость подъема груза через угловую скорость вала двигателя (или наоборот)  , где
, где 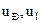 -передаточное число редуктора и кратность полиспаста,
-передаточное число редуктора и кратность полиспаста,  -диаметр барабана. Приравняв выражения для Т8, получим
-диаметр барабана. Приравняв выражения для Т8, получим  .
. , а в заменяющем
, а в заменяющем  , что с учетом
, что с учетом  , дает выражение для момента инерции барабана, приведенного к первому валу
, дает выражение для момента инерции барабана, приведенного к первому валу  . Остальные моменты инерции, входящие в момент
. Остальные моменты инерции, входящие в момент  , остаются неизменными.
, остаются неизменными. , а в заменяющем
, а в заменяющем 
 . Учитывая, что
. Учитывая, что 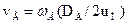 , получим
, получим  .
.
 ,
, , (7)
, (7)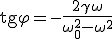 . (8)
. (8)

 , а если к более тихоходному, то умножить на
, а если к более тихоходному, то умножить на 
 - приведенный к первому валу (валу двигателя) момент статического сопротивления, Mст - момент статического сопротивления на произвольном валу механизма.
- приведенный к первому валу (валу двигателя) момент статического сопротивления, Mст - момент статического сопротивления на произвольном валу механизма.
 - КПД в тормозном режиме.
- КПД в тормозном режиме.

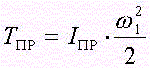

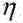 2...
2... 
 - радиус рабочего органа.
- радиус рабочего органа.



 ) и учитывается коэффициентом
) и учитывается коэффициентом 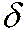 = 1,1...1,2.
= 1,1...1,2.
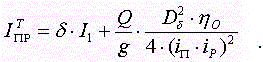
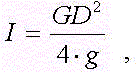
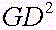 - маховой момент.
- маховой момент.

 - сумма маховых моментов масс, находящихся на быстроходном валу механизма.
- сумма маховых моментов масс, находящихся на быстроходном валу механизма.
 .
.


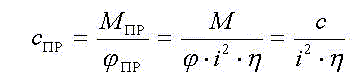
 ,
, будет соответствовать угол поворота барабана
будет соответствовать угол поворота барабана



 - передаточное отношение редуктора,
- передаточное отношение редуктора,  - кратность полиспаста.
- кратность полиспаста.


