
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вынужденные колебания. Резонанс. АвтоколебанияСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Колебания, совершающиеся под воздействием внешней периодической силы, называются вынужденными. В этом случае внешняя сила совершает положительную работу и обеспечивает приток энергии к колебательной системе. Она не дает колебаниям затухать, несмотря на действие сил трения. Периодическая внешняя сила может изменяться во времени по различным законам. Если свободные колебания происходят на частоте ω0, которая определяется параметрами системы, то установившиеся вынужденные колебания всегда происходят на частоте ω внешней силы. Уравнению, выражающему второй закон Ньютона для тела на пружине при наличии внешнего периодического воздействия, можно придать строгую математическую форму, если учесть связь между ускорением тела и его координатой:
где
Если частота ω внешней силы приближается к собственной частоте ω0, возникает резкое возрастание амплитуды вынужденных колебаний. Это явление называется резонансом. При резонансе амплитуда x m колебания груза может во много раз превосходить амплитуду y m колебаний свободного (левого) конца пружины, вызванного внешним воздействием. В отсутствие трения амплитуда вынужденных колебаний при резонансе должна неограниченно возрастать. В реальных условиях амплитуда установившихся вынужденных колебаний определяется условием: работа внешней силы в течение периода колебаний должна равняться потерям механической энергии за то же время из-за трения. Чем меньше трение (т. е. чем выше добротность Q колебательной системы), тем больше амплитуда вынужденных колебаний при резонансе.
Любая автоколебательная система состоит из 4 частей: 1. колебательная система; 2. источник энергии, компенсирующий потери энергии на преодоление сопротивления; 3. клапан – устройство, регулирующее поступление энергии в колебательную систему определенными порциями и в определенный промежуток времени; 4. обратная связь – устройство для обратного воздействия автоколебательной системы на клапан, управляющее работой клапана за счет процессов в самой колебательной системе. Волны и их характеристика Волна́ — возбуждение среды, распространяющееся в пространстве и времени или в фазовом пространстве с переносом энергии и без переноса массы По своему характеру волны подразделяются на: По признаку распространения в пространстве: стоячие, бегущие. По характеру волны: колебательные, уединённые (солитоны). По типу волн: поперечные, продольные, смешанного типа. По законам, описывающим волновой процесс: линейные, нелинейные. По свойствам субстанции: волны в дискретных структурах, волны в непрерывных субстанциях. По геометрии: сферические (пространственные), одномерные (плоские), спиральные. Характеристики волн Временна́я и пространственная периодичности временная периодичность — скорость изменения фазы с течением времени в какой-то заданной точке, называемую частотой волны Временная и пространственная периодичности взаимосвязаны. В упрощённом виде для линейных волн эта зависимость имеет следующий вид:
где c — скорость распространения волны в данной среде. Интенсивность волны Для характеристики интенсивности волнового процесса используют три параметра: амплитуда волнового процесса, плотность энергии волнового процесса и плотность потока энергии. Термодинамическая система и его параметры Термодинамические системы В термодинамике изучаются физические системы, состоящие из большого числа частиц и находящиеся в состоянии термодинамического равновесия или близком к нему. Такие системы называются термодинамическими системами. Единицей измерения числа частиц в термодинамической системе обычно служит число Авогадро[3] (примерно 6·10^23 частиц на моль вещества), дающее представление, о величинах какого порядка идёт речь. Термодинамическое равновесие — состояние системы, при котором остаются неизменными по времени макроскопические величины этой системы (температура,давление, объём, энтропия) в условиях изолированности от окружающей среды. Термодинамические параметры Различают экстенсивные параметры состояния, пропорциональные массе системы: объём, внутренняя энергия, энтропия, энтальпия, энергия Гиббса, энергия Гельмгольца (свободная энергия), и интенсивные параметры состояния, не зависящие от массы системы: давление, температура, концентрация, магнитная индукция и др. Законы идеального газа Закон Бойля - Мариотта. Пусть газ находится в условиях, когда его температура поддерживается постоянной (такие условия называются изотермическими).Тогда для данной массы газа произведение давления на объем есть величина постоянная:
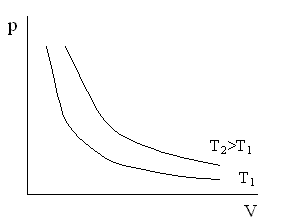
Эту формулу называют уравнением изотермы. Графически зависимость p от V для различных температур изображена на рисунке.
Закон Гей - Люссака. Пусть газ находится в условиях, когда постоянным поддерживается его давление (такие условия называются изобарическими). Их можно осуществить, если поместить газ в цилиндр, закрытый подвижным поршнем. Тогда изменение температуры газа приведет к перемещению поршня и изменению объема. Давление же газа останется постоянным. При этом для данной массы газа его объем будет пропорционален температуре:
Графически зависимость V от T для различных давлений изображена на рисунке.
Перейдя от температуры в шкале Цельсия к абсолютной температуре
Закон Шарля. Если газ находится в условиях, когда постоянным остается его объем (изохорические условия), то для данной массы газа давление будет пропорционально температуре: Закон Шарля также можно записать в виде:
Уравнение Клапейрона - Менделеева. Из законов идеального газа можно получить уравнение состояния, связывающее Т, р и V идеального газа в состоянии равновесия. Это уравнение впервые было получено французским физиком и инженером Б. Клапейроном и российским учеными Д.И. Менделеевым, поэтому носит их имя. Пусть некоторая масса газа занимает объем V1, имеет давление p1 и находится при температуре Т1. Эта же масса газа в другом состоянии характеризуется параметрами V2, p2, Т2 (см. рисунок). Переход из состояния 1 в состояние 2 осуществляется в виде двух процессов: изотермического (1 - 1') и изохорического (1' - 2).
Для данных процессов можно записать законы Бойля - Мариотта и Гей - Люссака:
Основное уравнения мкт
|
|||||||||||||
|
Последнее изменение этой страницы: 2016-04-20; просмотров: 673; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.15.91 (0.009 с.) |

 Тогда уравнение вынужденных колебаний запишется в виде
Тогда уравнение вынужденных колебаний запишется в виде
 – собственная круговая частота свободных колебаний, ω – циклическая частота вынуждающей силы
– собственная круговая частота свободных колебаний, ω – циклическая частота вынуждающей силы ;
;


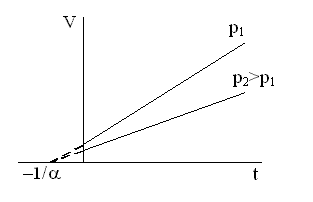
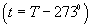 , закон Гей - Люссака можно записать в виде:
, закон Гей - Люссака можно записать в виде:







