
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Момент инерции математической точки, тело относительно неподвижной оси(от чего зависить)Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Моментом инерции системы (тела) относительно оси вращения называется физическая величина, равная сумме произведений масс n материальных точек системы на квадраты их расстояний до рассматриваемой оси:
В случае непрерывного распределения масс эта сумма сводится к интегралу
Момент инерции материальной точки: относительно данной оси – скалярная величина, равная произведению массы точки на квадрат расст. от этой точки до оси (J=mr2, m – масса точки; r – расстояние от точки до оси) Теорема Штейнера Теорема Штейнера — формулировка Согласно теореме Штейнера, установлено, что момент инерции тела при расчете относительно произвольно оси соответствует сумме момента инерции тела относительно такой оси, которая проходит через центр масс и является параллельной данной оси, а также плюс произведение квадрата расстояния между осями и массы тела, по следующей формуле (1): J= J0 + md2 (1) Где в формуле принимаем соответственно величины: d – расстояние между осями ОО1║О’O1’; J0 = Jd = mR2/2 (2) Например, для обруча на рисунке момент инерции относительно оси O’O’, равен
Момент инерции прямого стержня длиной
10) момент импульса закон сохранения момента импульса Моментом импульса (количества движения) материальной точки А относительно неподвижной точки О называется физическая величина, определяемая векторным произведением:
где r - радиус-вектор, проведенный из точки О в точку A, p =m v - импульс материальной точки (рис. 1); L - псевдовектор,
Рис.1
Моментом импульса относительно неподвижной оси z называется скалярная величина Lz, равная проекции на эту ось вектора момента импульса, определенного относительно произвольной точки О данной оси. Момент импульса Lz не зависит от положения точки О на оси z. При вращении абсолютно твердого тела вокруг неподвижной оси z каждая точка тела движется по окружности постоянного радиуса ri со скоростью vi. Скорость vi и импульс mivi перпендикулярны этому радиусу, т. е. радиус является плечом вектора mivi. Значит, мы можем записать, что момент импульса отдельной частицы равен
и направлен по оси в сторону, определяемую правилом правого винта. Зако́н сохране́ния моме́нта и́мпульса Математически выражается через векторную сумму всех моментов импульса относительно выбранной оси для замкнутой системы тел, которая остается постоянной, пока на систему не воздействуют внешние силы. В соответствии с этим момент импульса замкнутой системы в любой системе координат не изменяется со временем. Закон сохранения момента импульса есть проявление изотропности пространства относительно поворота. В упрощённом виде:
Основной закон сохранения, динамика твердого тела Динамика твердого тела Вращение вокруг неподвижной оси. Момент импульса твердого тела относительно неподвижной оси вращения равен
называется моментом инерции твердого тела относительно Продифференцировав
Это уравнение называют основным уравнением динамики вращательного движения твердого тела вокруг неподвижной оси. Вычислим еще кинетическую энергию вращающегося твердого тела:
и работу внешней силы при повороте тела:
Плоское движение твердого тела. Плоское движение есть суперпозиция поступательного движенияцентра масс и вращательного движения в системе центра масс (см. разд. 1.2). Движение центра масс описываетсявторым законом Ньютона и определяется результирующей внешней силой (уравнение (11)).Вращательное движение в системе центра масс подчиняется уравнению (39), в котором надо учитывать только реальные внешние силы, так как момент сил инерции относительно центра масс равен нулю (аналогично моменту сил тяжести, пример 1 из разд. 1.6). Кинетическая энергия плоского движения равна Движение с неподвижной точкой. Угловая скорость вращения, направленная вдоль оси вращения, меняет свое направление как в пространстве, так и по отношению к самому твердому телу. Уравнение движения
которое называют основным уравнением движения твердого тела с неподвижной точкой, позволяетузнать, как изменяется момент импульса
Рис. 11. замыкания уравнений движения надо научиться связывать эти величины друг с другом.
Рис. 12. Гироскопы. Гироскопом называют твердое тело, быстро вращающееся относительно своей оси симметрии. Задачу о движении оси гироскопа можно решать в гироскопическом приближении: На тяжелый гироскоп (рис. 12), у которого центр масс смещен на расстояние Конец вектора
Угловая скорость прецессии не зависит от угла наклона оси а. Зако́ны сохране́ния — фундаментальные физические законы, согласно которым при определённых условиях некоторые измеримые физические величины, характеризующие замкнутую физическую систему, не изменяются с течением времени. · Закон сохранения энергии · Закон сохранения импульса · Закон сохранения момента импульса · Закон сохранения массы · Закон сохранения электрического заряда · Закон сохранения лептонного числа · Закон сохранения барионного числа · Закон сохранения чётности Момент силы Моментом силы относительно оси вращения называется физическая величина, равная произведению силы на ее плечо. Момент силы определяют по формуле: М - FI, где F — сила, I — плечо силы. Плечом силы называется кратчайшее расстояние от линии действия силы до оси вращения тела. Момент силы характеризует вращающее действие силы. Это действие зависит как от силы, так и от плеча. Чем больше плечо, тем меньшую силу надо приложить, За единицу момента силы в СИ принимается момент силы в 1 Н, плечо которой равно 1м — ньютон-метр (Н • м). Правило моментов Твердое тело, способное вращаться вокруг неподвижной оси, находится в равновесии, если момент силы М,, вращающей его по часовой стрелке, равен моменту силы М2, вращающей его против часовой стрелки: М1 = -М2 или F 1 ll = - F 2 l 2. Момент пары сил одинаков относительно любой оси, перпендикулярной к плоскости пары. Суммарный момент М пары всегда равен произведению одной из сил F на расстояние I между силами, которое называется плечом пары, независимо от того, на какие отрезки и /2 разделяет положение оси плечо пары: M = Fll + Fl2=F(l1 + l2) = Fl.
Работа момента сил. Работа силы. Работа момента сил, действующего на тело, вращающееся вокруг неподвижной оси Механические колебания. Колеба́ния — повторяющийся в той или иной степени во временипроцесс изменения состояний системы. Колебания почти всегда связаны с попеременным превращением энергии одной формы проявления вдругую форму.
Отличие колебания от волны.
Колебания различной физической природы имеют много общих закономерностей и тесно взаимосвязаны cволнами. Поэтому исследованиями этих закономерностей занимается обобщённая теория колебаний иволн. Принципиальное отличие от волн: при колебаниях не происходит переноса энергии, это, так сказать, «местные» преобразования энергии. Характеристики колебаний Амплитуда Промежуток времени Число колебаний в единицу времени называется частотой колебаний Период колебаний
В круговых или циклических процессах вместо характеристики «частота» используется понятие круговая илициклическая частота
Фаза колебаний -- определяет смещение в любой момент времени, т.е. определяет состояниеколебательной системы.
Маятник мат физ пруж . Пружинный маятник — это груз массой m, который подвешен на абсолютно упругой пружине и совершает гармонические колебания под действием упругой силы F = –kx, где k — жесткость пружины. Уравнение движения маятника имеет вид
или
Из формулы (1) вытекает, что пружинный маятник совершает гармонические колебания по закону х = Асоs(ω0t+φ) с циклической частотой
и периодом
Формула (3) верна для упругих колебаний в границах, в которых выполняется закон Гука, т. е. если масса пружины мала по сравнению с массой тела. Потенциальная энергия пружинного маятника, используя (2) и формулу потенциальной энергии предыдущего раздела, равна
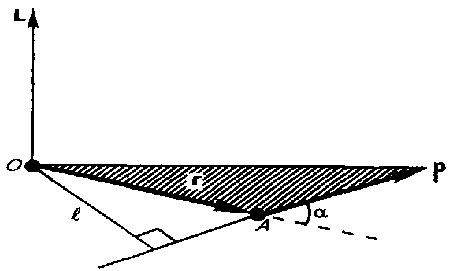
2. Физический маятник — это твердое тело, которое совершает колебания под действием силы тяжести вокруг неподвижной горизонтальной оси, которая проходит через точку О, не совпадающую с центром масс С тела (рис. 1).
Рис.1
Если маятник из положения равновесия отклонили на некоторый угол α, то, используя уравнение динамики вращательного движения твердого тела, момент M возвращающей силы
где J — момент инерции маятника относительно оси, которая проходит через точку подвеса О, l – расстояние между осью и центром масс маятника, Fτ ≈ –mgsinα ≈ –mgα — возвращающая сила (знак минус указывает на то, что направления Fτ и α всегда противоположны; sinα ≈ α поскольку колебания маятника считаются малыми, т.е. маятника из положения равновесия отклоняется на малые углы). Уравнение (4) запишем как
или
Принимая
получим уравнение
идентичное с (1), решение которого (1) найдем и запишем как:
Из формулы (6) вытекает, что при малых колебаниях физический маятник совершает гармонические колебания с циклической частотой ω0 и периодом
где введена величина L=J/(m l) — приведенная длина физического маятника. Точка О' на продолжении прямой ОС, которая отстоит от точки О подвеса маятника на расстоянии приведенной длины L, называется центром качаний физического маятника (рис. 1). Применяя теорему Штейнера для момента инерции оси, найдем
т. е. ОО' всегда больше ОС. Точка подвеса О маятника и центр качаний О' имеют свойство взаимозаменяемости: если точку подвеса перенести в центр качаний, то прежняя точка О подвеса будет новым центром качаний, и при этом не изменится период колебаний физического маятника. 3. Математический маятник — это идеализированная система, состоящая из материальной точки массой m, которая подвешена на нерастяжимой невесомой нити, и которая колеблется под действием силы тяжести. Хорошее приближение математического маятника есть небольшой тяжелый шарик, который подвешен на длинной тонкой нити. Момент инерции математического маятника
где l — длина маятника. Поскольку математический маятник есть частный случай физического маятника, если предположить, что вся его масса сосредоточена в одной точке — центре масс, то, подставив (8) в (7), найдем выражение для периода малых колебаний математического маятника
Сопоставляя формулы (7) и (9), видим, что если приведенная длина L физического маятника равна длине l математического маятника, то периоды колебаний этих маятников одинаковы. Значит, приведенная длина физического маятника — это длина такого математического маятника, у которого период колебаний совпадает с периодом колебаний данного физического маятника. Гар. колебания и харак. Колебаниями называются движения или процессы, характеризующиеся определенной повторяемостью во времени. Колебательные процессы имеют широкое распространение в природе и технике, например качание маятника часов, переменный электрический ток и т. Д
где ω0 — круговая (циклическая) частота, А - максимальное значение колеблющейся величины, называемое амплитудой колебания, φ — начальная фаза колебания в момент времени t=0, (ω0t+φ) - фаза колебания в момент времени t. Фаза колебания есть значение колеблющейся величины в данный момент времени. Так как косинус имеет значение в пределах от +1 до –1, то s может принимать значения от +А до –А. Определенные состояния системы, которая совершает гармонические колебания, повторяются через промежуток времени Т, имеющий название период колебания, за который фаза колебания получает приращение (изменение) 2π, т. е.
откуда
Величина, обратная периоду колебаний,
т. е. число полных колебаний, которые совершаются в единицу времени, называется частотой колебаний. Сопоставляя (2) и (3), найдем
Единица частоты — герц (Гц): 1 Гц — частота периодического процесса, во время которого за 1 с совершается один цикл процесса.
Амплитуда колебаний Амплитудой гармонического колебания называется наибольшее значение смещения тела от положения равновесия. Амплитуда может принимать различные значения. Она будет зависеть от того, насколько мы сместим тело в начальный момент времени от положения равновесия. Амплитуда определяется начальными условиями, то есть энергией сообщаемой телу в начальный момент времени. Так как синус и косинус могут принимать значения в диапазоне от -1 до 1, то в уравнении должен присутствовать множитель Xm, выражающий амплитуду колебаний. Уравнение движения при гармонических колебаниях: x = Xm*cos(ω0*t). Затух. колеб и их хар Затухающие колебания Затуханием колебаний называется постепенное уменьшение амплитуды колебаний с течением времени, обусловленное потерей энергии колебательной системой. Собственные колебания без затухания – это идеализация. Причины затухания могут быть разные. В механической системе к затуханию колебаний приводит наличие трения. В электромагнитном контуре к уменьшению энергии колебаний приводят тепловые потери в проводниках, образующих систему. Когда израсходуется вся энергия, запасенная в колебательной системе, колебания прекратятся. Поэтому амплитуда затухающих колебаний уменьшается, пока не станет равной нулю. где β – коэффициент затухания,, где ω0 – частота незатухающих свободных колебаний в отсутствии потерь энергии в колебательной системе. В новых обозначениях дифференциальное уравнение затухающих колебаний имеет вид:
Это линейное дифференциальное уравнение второго порядка. Частота затухающих колебаний: В любой колебательной системе затухание приводит к уменьшению частоты и соответственно увеличению периода колебаний.
Период затухающих колебаний:
Смысл, который вкладывался в понятие периода для незатухающих колебаний, не подходит для затухающих колебаний, так как колебательная система никогда не возвращается в исходное состояние из-за потерь колебательной энергии. При наличии трения колебания идут медленнее: Периодом затухающих колебаний называется минимальный промежуток времени, за который система проходит дважды положение равновесия в одном направлении. Амплитуда затухающих колебаний:
Амплитуда затухающих колебаний – величина не постоянная, а изменяющаяся со временем тем быстрее, чем больше коэффициент β. Поэтому определение для амплитуды, данное ранее для незатухающих свободных колебаний, для затухающих колебаний надо изменить. При небольших затуханиях амплитудой затухающих колебаний называется наибольшее отклонение от положения равновесия за период. Изменение амплитуды затухающих колебаний происходит по экспоненциальному закону:
Пусть за время τ амплитуда колебаний уменьшится в "e " раз ("е" – основание натурального логарифма, е ≈ 2,718). Тогда, с одной стороны,
Вынужденные колеб.
|
|||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-20; просмотров: 2493; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.151.127 (0.009 с.) |



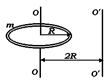

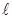 , ось перпендикулярна стержню и проходит через его конец.
, ось перпендикулярна стержню и проходит через его конец.

 (1)
(1) , если система находится в равновесии.
, если система находится в равновесии.
 Направление проекции совпадает с направлением т.е. определяется по правилу буравчика. Величина
Направление проекции совпадает с направлением т.е. определяется по правилу буравчика. Величина



 уравнение
уравнение  Момент импульса относительно неподвижной оси, перпендикулярной плоскости движения, вычисляется по формуле (см. уравнение
Момент импульса относительно неподвижной оси, перпендикулярной плоскости движения, вычисляется по формуле (см. уравнение  где
где  — плечо скорости центра масс относительно оси, а знаки определяются выбором положительного направления вращения.
— плечо скорости центра масс относительно оси, а знаки определяются выбором положительного направления вращения.
 Так как вектор
Так как вектор  в общем случае не параллелен вектору
в общем случае не параллелен вектору  то для
то для
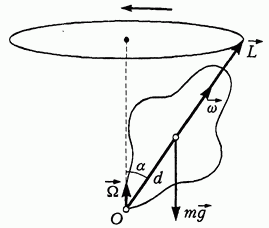
 оба вектора направлены вдоль оси симметрии. Уравновешенный гироскоп (закрепленный в центре масс) обладает свойством безынерционно
оба вектора направлены вдоль оси симметрии. Уравновешенный гироскоп (закрепленный в центре масс) обладает свойством безынерционно  его ось перестает двигаться, как только исчезает внешнее воздействие (
его ось перестает двигаться, как только исчезает внешнее воздействие ( обращается в нуль). Это позволяет использовать гироскоп для сохранения ориентации в пространстве.
обращается в нуль). Это позволяет использовать гироскоп для сохранения ориентации в пространстве. от точки закрепления действует момент силы тяжедти, направленный перпендикулярно
от точки закрепления действует момент силы тяжедти, направленный перпендикулярно  Так как
Так как  то
то  и ось гироскопа совершают регулярное вращение вокруг вертикальной оси (прецессия гироскопа).
и ось гироскопа совершают регулярное вращение вокруг вертикальной оси (прецессия гироскопа). вращается по горизонтальной окружности радиусом
вращается по горизонтальной окружности радиусом  а с угловой скоростью
а с угловой скоростью
 ,
,
 , то линейная скорость i -й точки
, то линейная скорость i -й точки  , Ri – расстояние до оси вращения. Следовательно,
, Ri – расстояние до оси вращения. Следовательно, ,
,
 ,
,
 , где
, где  — перемещение тела,
— перемещение тела,  — сила, действующая на тело.
— сила, действующая на тело. 
 . Работа измеряется в Джоулях [Дж].
. Работа измеряется в Джоулях [Дж]. , где
, где 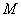 — момент силы,
— момент силы,  — угол поворота.
— угол поворота. .
. (м) — максимальное отклонение колеблющейся величины от некоторого усреднённого еёзначения для системы.
(м) — максимальное отклонение колеблющейся величины от некоторого усреднённого еёзначения для системы. (сек), через который повторяются какие-либо показатели состояния системы(система совершает одно полное колебание), называют периодом колебаний.
(сек), через который повторяются какие-либо показатели состояния системы(система совершает одно полное колебание), называют периодом колебаний. (Гц, сек-1).
(Гц, сек-1). и
и 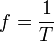
 (Гц, сек-1, об/сек), показывающая число колебаний за время 2π:
(Гц, сек-1, об/сек), показывающая число колебаний за время 2π:


 (2)
(2) (3)
(3)

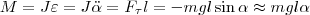 (4)
(4)

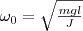 (5)
(5)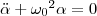
 (6)
(6) (7)
(7)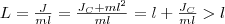
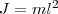 (8)
(8)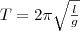 (9)
(9) (1)
(1)
 (2)
(2) (3)
(3)
 . где β – коэффициент затухания,, где ω0 – частота незатухающих свободных колебаний в отсутствии потерь энергии в колебательной системе.
. где β – коэффициент затухания,, где ω0 – частота незатухающих свободных колебаний в отсутствии потерь энергии в колебательной системе. (физический смысл имеет только вещественный корень, поэтому
(физический смысл имеет только вещественный корень, поэтому  ).
). .
. .
. , для пружинного маятника
, для пружинного маятника  .
.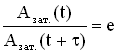 , а с другой стороны, расписав амплитуды Азат.(t) и Азат.(t+τ), имеем
, а с другой стороны, расписав амплитуды Азат.(t) и Азат.(t+τ), имеем 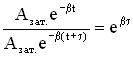 . Из этих соотношений следует βτ = 1, отсюда
. Из этих соотношений следует βτ = 1, отсюда .
.


