
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Энергия затухающих колебанийСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
Энергия затухающих колебаний
Энергию осциллятора с потерями энергии можно рассчитать с помощью тех же формул, которые получены для идеального осциллятора. Особенностью реального осциллятора является то, что амплитуда его колебаний с течением времени уменьшается. Поскольку полная энергия осциллятора прямо пропор-циональна квадрату амплитуды, постольку и полная энергия реального осциллятора будет уменьшаться с течением времени. Выражения для расчёта энергии реального осциллятора имеют следующий вид: для пружинного маятника
энергия математического маятника с потерями энергии
Энергия, запасённая в колебательном контуре, сопротивление которого отлично от нуля, может быть найдена следующим образом:
Таким образом, полная энергия осциллятора с потерями энергии уменьшается с течением времени по экспоненциальному закону. Обратите внимание: скорость уменьшения энергии осцил-лятора в два раза выше скорости уменьшения амплитуды колебаний осциллятора.
Вынужденные колебания
Любой осциллятор (например, пружинный маятник) может испытывать внешнее воздействие. Если внешнее воздействие периодическое, то возникнут вынужденные колебания осцил-лятора. Характер колебаний осциллятора определяется как внеш-ним воздействием, так и свойствами осциллятора.
Вынужденные колебания в колебательном Контуре
В соответствии со вторым правилом Кирхгофа, сумма разностей потенциалов на элементах контура равна сумме эдс, дей-ствующих в рассматриваемом кон-туре. В рассматриваемом колебательном контуре два источника эдс – это источ-ник переменной эдс e и соленоид (в нём возникает эдс самоиндукции eL). На обкладках заряженного конденсатора имеется разность потенциалов. Обозначим её UC. Разность потенциалов на концах резистора, в соответствии с законом Ома, равна IR. Тогда уравнение, описывающее колебательный контур, имеет следующий вид:
Поскольку разность потенциалов на обкладках конденсатора
или
учитывая, что
и после деления на L
Вводя обозначения
Мы вновь получили неоднородное дифференциальное уравне-ние второго порядка. Полученное дифференциальное уравнение ничем не отличается от того, которое получено для пружинного маятника в предыдущем разделе. Следовательно, его решение имеет такой же вид: Это означает, что в колебательном контуре, содержащем источник переменной эдс, изменяющейся по гармоническому закону, будут происходить вынужденные колебания с частотой, равной частоте колебаний вынуждающей эдс.
Явление резонанса
Рассмотрим зависимость амплитуды вынужденных колебаний от частоты внешнего воздействия и параметров осциллятора более подробно. Из выражения амплитуда вынужденных колебаний зависит от частоты внешнего воздействия w. Можно показать, что эта функция имеет экстремум, т. е. при определённой частоте амплитуда вынуж-денных колебаний будет максимальной. Это явление называют резонансом, а частоту вынужденных колебаний, при которой амплитуда максимальна – резонансной частотой. При резонансной частоте амплитуда максимальна, а знаменатель выражения, показывающего величину амплитуды, минимален. Найдём эту частоту. Знаменатель имеет экстремум при частоте внешнего воздействия, на которой производная от знаменателя по частоте w равна нулю:
Полученное выражение будет равно нулю при двух значениях частоты внешнего воздействия: w = 0 и Если w = 0, то колебаний нет, поэтому первый корень уравнения отбрасываем. Второй же корень и есть резонансная частота wрез. Именно при частоте внешнего воздействия
При слабом затухании (
Обратите внимание на то, что значение b достаточно сильно влияет на амплитуду при резо-нансе (см. рисунок): чем больше потери, тем меньше резонансная амплитуда. При отклонении частоты внешнего воздействия от резо-нансной амплитуда вынужден-ных колебаний уменьшается (см. рисунок). Теперь найдём амплитуду вынужденных колебаний для низких (w<<wо) и высоких (w>>wо) частот внешнего воз-действия. При w<<wо амплитуда вы-нужденных колебаний будет приблизительно равна:
если затухание мало (
где k – коэффициент упругости пружины. В полученном выражении отсутствует частота внешнего воздействия. Это значит, что при малых частотах внешнего воздействия колебательная система реагирует на гармоническую внешнюю силу практически как на статическую, т. е. не изменяющуюся с течением времени. Амплитуда вынужденных колебаний определяется величиной внешнего воздействия и упругими свойствами осциллятора. При высоких частотах (w>>wо). и при
Таким образом, при высокой частоте внешнего воздействия максимальное отклонение от положения равновесия А опре-деляется величиной внешнего воздействия, инертностью осцил-лятора и частотой воздействия. Упругие свойства колебательной системы не имеют никакого значения (поскольку в выражении отсутствует wо).
Добротность
Добротность используется для характеристики колебательных систем. Добротность определяют как отношение амплитуды вынуж-денных колебаний при резонансе А рез к амплитуде при низкой частоте А стат
Используя полученные в разд. 8.3 выражения для А рез и А стат, получаем
Добротность показывает, во сколько раз амплитуда при резонансе больше амплитуды вынужденных колебаний при низких частотах. Следовательно, чем больше добротность, тем сильнее проявляет себя резонанс при вынужденных колебаниях. Можно сказать и иначе: чем меньше потери энергии, тем сильнее резонанс.
От частоты
Вынужденные колебания описываются уравнением
где
Нетрудно получить, что при w = 0 j = arctg0 = 0 радиан. При w = wо j = arctg¥ = p/2. При w > wо j ® p. Таким образом, при резонансе колебания х отстают по фазе от внешнего воздействия на p/2. Други-ми словами – сила достигает мак-симального значения в те моменты, когда смещение от положения равновесия равно нулю. В этот момент осциллятор имеет максимальную скорость. Наибольшее воздействие именно в этот момент увеличивает ско-рость осциллятора, и поэтому он наиболее сильно раскачивается.
Волны Упругие волны
Если вызвать колебания одной частицы среды (твёрдой, жидкой или газообразной), то в колебательное движение начнут вовлекаться и окружающие частицы. Таким образом, в упругой среде колебательный процесс теряет локальный характер. Колебания могут распространяться в пространстве. Этот процесс и называют волной. Упругая волна – это процесс распространения колебаний в среде. Обратите внимание на важную деталь: каждая из частиц среды колеблется вокруг своего равновесного положения. Волна не вызывает переноса частиц среды. Она лишь вовлекает в колебательный процесс всё новые и новые частицы. Энергия колеблющейся частицы больше, чем энергия такой же покоящейся частицы. Поэтому вовлечение в колебательный процесс новых частиц среды означает, что их энергия возрастает. Это значит, что волна переносит энергию. В зависимости от того, как взаимно ориентированы направ-ление распространения волны и направление колебаний частиц, различают продольные и поперечные волны. Продольными называют волны, в которых направление колебаний частиц и направление распространения волны совпа-дают. Поперечными называют волны, в которых направление колебаний частиц и направление распространения волны взаимно перпендикулярны.
Поперечные упругие волны возможны лишь в тех средах, где частицы достаточно сильно связаны между собой. Такой средой являются твёрдые тела и, в определённой степени, жидкости. В газах связь молекул пренебрежимо мала. Поэтому поперечные упругие волны возникают лишь в твёрдых телах.* Если колебания частиц происходят по гармоническому закону, волна называется гармонической. Как уже отмечалось, волна есть процесс распространения колебаний в пространстве. Это означает, что существуют точки, до которых колебания ещё не дошли. Совокупность точек, до которых к моменту време-ни t дошли колебания, называют фронтом волны. Фронт волны перемещается в пространстве со скоростью распространения волны. При описании волн удобно пользоваться понятием волновая поверхность. Это геометрическое место точек среды, колеб-лющихся в одной фазе. Волновую поверхность можно провести через любую точку среды, охваченной волновым процессом. Поэтому можно построить любое количество волновых поверхностей. Поскольку все точки волновой поверхности колеблются в одной фазе во все моменты времени, волновая поверхность неподвижна. Волновая поверхность может иметь различную форму. В про-стейших случаях это плоскость, сфера. Волны с плоской волновой поверхностью называют плоскими. Волны со сферической волновой поверхностью называют сферическими.
______________________________
* В жидкостях тоже могут возникнуть поперечные волны, но из-за слабой связи между молекулами они быстро затухают. Фазовая скорость
Вернёмся к уравнению Выделим из него фазу
Пусть фаза имеет фиксированное значение, т. е. j = con st. Тогда
или
т. е. фазу, которую в момент t имела частица среды, находящаяся на расстоянии х от источника волны, через dt секунд будет иметь частица, находящаяся на dx метров дальше. Другими словами, любое постоянное значение фазы перемещается, удаляясь от источника. Сокращая w в последнем выражении, получаем
______________________________
* Физический смысл производной – скорость изменения функции по изменению ее аргумента.
Таким образом скорость v является скоростью, с которой перемещается фиксированное значение фазы. Поэтому её называют фазовой скоростью. Волновое число k по определению равно
Отметим ещё одну деталь. Величина отношения w/ k зависит от значения частоты, поэтому фазовая скорость волн разных частот будет разной. Такое явление действительно существует и называется дисперсией волн. Среды, в которых имеет место дисперсия, называют диспергирующими.
Волновое уравнение
Волновым называют дифференциальное уравнение, описы-вающее процесс распространения гармонических волн в среде. Найдём вид этого уравнения в простейшем случае – для плоской бегущей волны, распространяющейся параллельно оси х,
Возьмём вторые производные от x по времени и координате:
Учитывая, что
Таким образом, если анализ некоторой системы приводит нас к дифференциальному уравнению Уравнение волны Обратите внимание: волновое уравнение не следует путать с уравнением волны. Волновое уравнение описывает процесс распространения гармонических колебаний в некоторой среде. Уравнение волны показывает, как смещены от положения равновесия частицы упругой среды в зависимости от t и х.
Энергия упругой волны
Пусть вдоль оси х распространяется плоская волна
Выделим некоторый малый объём D V в пределах которого скорость движения колеблющихся частиц Тогда кинетическая энергия частиц в этом объёме
где r – плотность упругой среды. Можно показать, что потенциальная энергия упругой деформации этого объёма
где v – фазовая скорость волны.
Полная энергия равна сумме кинетической и потенциальной энергий:
Объёмная плотность энергии, равная энергии единичного объёма
Поскольку
и
Так как
и, наконец,
Как известно, среднее значение квадрата синуса равно 1/2. Следовательно, среднее значение плотности энергии
Отсюда видно, что среднее значение плотности энергии зависит от плотности среды, амплитуды колебаний и цикли-ческой частоты волны. Вообще же плотность энергии волны различна в разные моменты времени в одной точке пространства и в один момент времени в разных точках пространства. Эта энергия испускается источником колебаний и переносится волной в пространстве. Кроме объёмной плотности энергии используется плотность потока энергии j, которая равна энергии, перенесённой волной через единичную поверхность D Sn, перпендикулярную направ-лению распространения волны, за единицу времени. В аналитической форме определение плотности потока энергии имеет вид
где D Е – энергия, переносимая за время D t через площадку D Sn, перпендикулярную к скорости распространения волны. В случае плоской волны
Тогда
или, векторной форме,
Вектор j называют вектором Умова. Этот вектор показывает, какая энергия передаётся волной за единицу времени через единицу площади и в каком направлении она распространяется. Как видите, направление переноса энергии определяется ско-ростью волны – энергия переносится волной в направлении распространения волны.
Групповая скорость
В науке и технике волны широко используются для передачи информации. Однако гармоническая волна способна донести информацию лишь о том, что где-то есть источник волны. Для того чтобы с помощью волн можно было передавать необходимое количество информации, их необходимо изменять (например, испускать волны в виде импульсов, или изменять амплитуду волны, её частоту, начальную фазу). Такая волна называется модулированной. С помощью модулированных упругих волн определяют глубину морей и океанов (эхолот), а модулированные электро-магнитные волны позволяют осуществлять радио- и телевещание. Но если модулированные волны отличаются от гармони-ческих способностью переносить информацию, то, возможно, им присущи и другие отличия. Исследуем один из аспектов этой проблемы – найдём скорость, с которой модулированная волна переносит энергию. Для этого рассмотрим две одинаково направленные плоские поперечные бегущие волны, колебания которых происходят в одной плоскости, амплитуды которых равны, а частоты почти одинаковы. Тогда
Эту волну можно представить в виде
где
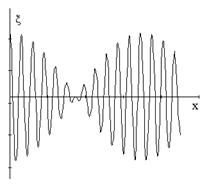
т. е. это волна с медленно изменяющейся амплиту-дой, или модулированная, такая же, как на рисунке. Показанная здесь кар-тина соответствует како-му-то моменту времени. В следующий момент она сдвинется вправо. Найдём скорость, с ко-торой модулированная волна будет распространяться. Для простоты рассмотрим точку, в которой амплитуда максимальна, – скорость перемещения этой точки равна скорости модулиро-ванной волны. Поведение точки с максимальной амплитудой описывается выражением Для любой бегущей волны
где v 1 и v 2 – фазовые скорость волн с циклическими частотами w1 и w2 соотвественно. Если дисперсии нет, то v 1 = v 2 = v и Если же среда диспергирующая, то Если вспомнить, что энергия колебаний пропорциональна квадрату амплитуды, то легко сообразить, что бóльшая часть энергии, переносимой такой волной, сконцентрирована там, где амплитуда волны велика. Это означает, что полученная скорость u есть скорость передачи энергии. Эту скорость u и называют групповой:
Важно отметить, что фронт волны распространяется с групповой скоростью.
Электромагнитные волны
К середине XIX в. был открыт ряд важнейших законов в области электричества и магнетизма. Значительная часть открытий в этой области принадлежит Майклу Фарадею. Этот крупнейший учёный, по праву считающийся осново-положником современной электродинамики, как это ни странно, не знал математики. Поэтому открытые им явления не имели математического описания. В 1854 г. в Кембриджский университет был принят на работу только что закончивший его Джеймс Клерк Максвелл. Основной целью своей деятельности он избрал математическое описание открытий Фарадея. Это ему удалось (см. разд. 5.6, 5.7). Один из результатов деятельности Максвелла – предсказание о существовании электромагнитных волн. Примерно через двадцать лет после этого электромагнитные волны были получены экспериментально немецким физиком Генрихом Герцем. Рассмотрим механизм возникновения и некоторые особенности электромагнитных волн. Допустим, что электрическое поле в вакууме создано зарядом, совершающим гармонические колебания. Электрическое поле, созданное таким зарядом, также должно изменяться с течением времени по гармоническому закону. Плотность тока смещения, созданного изменяющимся электрическим полем, равна Ток смещения создаёт магнитное поле
Важно отметить, что изменение электрического и магнитного полей опи-сывается одной и той же гармонической функцией. Ток смещения Вектор индукции магнитного поля всегда перпендикулярен создавшему его току. Это означает, что магнитное поле, созданное изменяющимся электрическим полем, будет перпендикулярно ему. В соответствии с уравнением Максвелла о циркуляции вектора Е, изменяющееся магнитное поле порождает электри-ческое. Причём порождаемое электрическое поле будет перпен-дикулярно изменяющемуся магнитному.
Более строгий анализ позволяет пока-зать, что изменяющиеся электрическое и магнитное поля описываются волновыми уравнениями:
где с – скорость света в вакууме (если электромагнитная волна распространяется в среде, то используется скорость света в этой среде). Решение этих уравнений имеет следующий вид:
где амплитуды Е и Н связаны соотношением
Можно также показать, что если вектор Е па-раллелен оси х, а вектор В параллелен оси у, то электромагнитная волна распро-страняется вдоль оси z (см. рису-нок). Другими словами, векторы Е, Н и вектор скорости электро-магнитной волны с образуют правую тройку. Важно отметить, что колеба-ния Е и Н синфазны. Вектор Умова–Пойнтинга
Электромагнитные волны, как и упругие волны, переносят энергию. Эта энергия складывается из энергии, перенесённой электрической и магнитной составляющими электромагнитной волны. Ранее мы установили, что плотность энергии электрического поля
а плотность энергии магнитного поля
Поэтому в любой момент времени плотность энергии электромагнитной волны
Поскольку Отсюда
и окончательно
Умножая объёмную плотность энергии электромагнитной волны на скорость её распространения, получим некоторую величину П = сw = EH. Размерность этой величины Так как векторы Е и Н взаимно перпендикулярны и образуют правую тройку с направлением распространения волны, направление вектора Поэтому вектор
ЛИТЕРАТУРА
1. Арсентьев В.В., Кирпиченков В.Я. и др. Курс физики. – СПб.: Лань, 2000. – Т. 1. 2. Баранов А.В., Невская Г.Е. и др. Колебания и волны. Оптика. Квантовая механика. – Новосибирск, 1993. 3. Барановский С.Н., Болдырев А.М. и др. Механика. Элект-ричество. Магнетизм. – Новосибирск: Изд-во НГТУ, 1995. 4. Горелик Г.С. Колебания и волны. – М.: ГИТТЛ, 1950. 5. Джанколи. Физика. – М.: Мир, 1989. – Т. 1, 2. 6. Калашников С.Г. Электричество – М.: Наука, 1970 7. Матвеев А.Н. Электричество и магнетизм. – М.: Высшая школа, 1983. 8. Орир. Физика. – М.: Мир, 1981. – Т. 1, 2. 9. Путилов К.А. Курс физики. – М.: ОГИЗ, 1945. 10. Савельев И.В. Курс общей физики. – М.: Наука, 1978. – Т. 1, 2. 11. Сивухин Д.В. Общий курс физики. –М.: Наука, 1977. – Т. 3. 12. Спасский Б.И. История физики. – М.: Высшая школа, 1977. – Т.1, 2 13. Трофимова Т.И. Курс физики. – М.: Высш. школа, 1990. 14. Физика. Большой энциклопедический словарь. – М.: Большая Российская Энциклопедия, 1999 15. Фриш С.Э., Тиморева А.В. Курс общей физики. – М.: Физматгиз, 1961. – Т. 2 16. Штрауф Е.А. Курс физики. – Л.: Судпромгиз, 1962.
ОГЛАВЛЕНИЕ 1. Электростатика.................................................................................... 3 1.1. Электрические заряды. Свойства электрических зарядов..... 3 1.2. Закон Кулона...................................................................................... 4 1.3. Электрическое поле. Напряжённость электрического поля... 5 1.4. Принцип суперпозиции.................................................................... 7 1.5. Поток вектора напряжённости....................................................... 9 1.6. Теорема Гаусса................................................................................ 10 1.7. Примеры расчёта напряжённости полей с помощью теоремы Гаусса................................................................................. 13 1.7.1. Поле бесконечной равномерно заряженной прямолинейной нити............................................................... 13 1.7.2. Поле бесконечной равномерно заряженной плоскости.................................................................................. 15 1.7.3. Поле двух параллельных равномерно заряженных плоскостей с одинаковым по величине и противоположным по знаку зарядом................................ 16 1.7.4. Поле равномерно заряженной сферы.............................. 17 1.8. Работа электростатических сил................................................ 18 1.9. Циркуляция вектора напряжённости....................................... 20 1.10. Потенциал электростатического поля.................................... 21 1.11. Связь напряжённости и потенциала......................................... 22 1.12. Графическое изображение электрического поля. Силовые линии. Эквипотенциальные поверхности............... 23 1.13. Электрический диполь. Диполь в однородном электрическом поле...................................................................... 25 1.14. Диэлектрики. Типы диэлектриков............................................ 26 1.15. Поляризация диэлектриков....................................................... 27 1.16. Поле в однородном диэлектрике.............................................. 30 1.17. Вектор электрического смещения. Теорема Гаусса для поля в диэлектрике................................................................ 32 1.18. Условия на границе раздела двух диэлектриков................. 34 1.19. Проводники в электрическом поле........................................... 37 1.20. Замкнутые проводящие оболочки........................................... 39 1.21. Электроёмкость уединённого проводника............................. 40 1.22. Конденсаторы................................................................................ 42 1.23. Соединение конденсаторов........................................................ 43 1.24. Энергия заряженных проводников........................................... 45 1.25. Энергия электрического поля.................................................... 46
2. Постоянный электрический ток........................................... 47 2.1. Электродвижущая сила.................................................................. 49 2.2. Закон Ома........................................................................................... 51 2.3. Работа и мощность тока. Закон Джоуля-Ленца...................... 53
3. Магнитное поле в вакууме....................................................... 54 3.1. Магнитное поле. Источник магнитного поля. Характеристики магнитного поля............................................... 54 3.2. Индукция магнитного поля, созданного движущимся точечным зарядом............................................................................ 55 3.3. Закон Био–Савара–Лапласа......................................................... 56 3.4. Расчёт магнитных полей с помощью закона Био–Савара–Лапласа...................................................................... 58 3.4.1. Индукция магнитного поля отрезка прямоли- нейного проводника с током...................................................... 58 3.4.2. Индукция магнитного поля бесконечно длинного 3.4.3. Индукция магнитного поля в центре квадрата..................... 60 3.4.4. Расчёт магнитного поля замкнутого кругового тока (витка с током)................................................................................. 61 3.5. Силовые линии магнитного поля................................................. 62 3.6. Сила Лоренца.................................................................................... 63 3.7. Сила Ампера...................................................................................... 66 3.8. Контур с током в однородном магнитном поле....................... 67 3.9. Магнитный поток. Работа, совершаемая при перемещении проводника с током в магнитном поле............. 69 3.10. Теорема Гаусса для магнитного поля...................................... 71 3.11. Закон полного тока........................................................................ 71 3.11.1.Магнитное поле бесконечного соленоида............................ 73 3.11.2. Магнитное поле тороида.......................................................... 76 3.12. Индуктивность соленоида........................................................... 76
4. Магнитное поле в веществе..................................................... 78 4.1. Намагничивание магнетика........................................................... 78 4.2. Напряжённость магнитного поля. Теорема о циркуляции вектора Н.................................................................................................... 79 4.3. Магнитомеханические явления.................................................... 82 4.3.1. Диамагнетики................................................................................. 84 4.3.2. Парамагнетики............................................................................... 84 4.4. Ферромагнетики. Природа ферромагнетизма.......................... 85 4.5. Намагничивание ферромагнетика. Этапы намагничивания 86 4.6. Явление гистерезиса....................................................................... 87 4.7. Граничные условия для векторов В и Н..................................... 88
5. Электромагнитная индукци.................................................... 92 5.1. Явление электромагнитной индукции....................................... 92 5.2. Природа электромагнитной индукции....................................... 94 5.3. Явление самоиндукции................................................................... 97 5.4. Взаимная индукция......................................................................... 98 5.5. Ток смещения.................................................................................. 100 5.6. Уравнение Максвелла для циркуляции вектора Н.............. 104 5.7. Уравнение Максвелла для циркуляции вектора Е................ 105 5.8. Энергия магнитного поля............................................................ 106
6. гармонические Колебания..................................................... 108 6.1. Гармонические колебания. Параметры гармонических колебаний............................................................ 108 6.2. Формы представления гармонических колебаний............... 109 6.3. Сложение гармонических колебаний...................................... 111 6.3.1. Сложение одинаково направленных гармонических колебаний с равными частотами..................................... 111 6.3.2. Сложение одинаково направленных колебаний с разными частотами. Биения............................................ 112 6.3.3. Сложение взаимно перпендикулярных колебаний.... 113 6.4. Гармонический осциллятор........................................................ 116 6.4.1. Пружинный маятник............................................................ 117 6.4.2. Математический маятник.................................................. 118 6.4.3. Колебательный контур....................................................... 120 6.5. Энергия гармонического осциллятора..................................... 121
7. Затухающие колебания............................................................. 124 7.1. Затухающие колебания пружинного маятника..................... 124 7.2. Затухающие колебания в колебательном контуре............... 126 7.3. Характеристики затухающих колебаний............................... 127 7.4. Критическое затухание............................................................... 129 7.5. Энергия затухающих колебаний.............................................. 130
8. Вынужденные колебания......................................................... 130 8.1. Вынужденные колебания пружинного маятника................. 131 8.2. Вынужденные колебания в колебательном контуре............ 134 8.3. Зависимость амплитуды вынужденных колебаний от частоты внешнего воздействия. Явление резонанса...... 135 8.4. Добротность..................................................................................... 138 8.5. Зависимость фазы вынужденных колебаний от частоты... 138
Волны........................................................................................................... 139 9.1. Упругие волны................................................................................. 139 | |||||||||||
|
| Поделиться: |

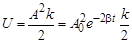 ;
;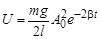 .
.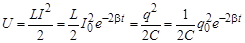 .
. Рассмотрим электрическую цепь, содержащую соленоид, кон-денсатор, резистор и источник переменной эдс, изменяющейся по гармоническому закону
Рассмотрим электрическую цепь, содержащую соленоид, кон-денсатор, резистор и источник переменной эдс, изменяющейся по гармоническому закону  .
.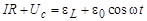 .
. , а эдс самоиндукции
, а эдс самоиндукции 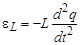 ,
,
 ;
; , получаем
, получаем
 .
. и
и  , получаем
, получаем .
. .
. видно, что
видно, что .
. .
. амплитуда вынужденных колебаний максимальна. Её значение
амплитуда вынужденных колебаний максимальна. Её значение
 .
. ) резонансную амплитуду можно считать равной
) резонансную амплитуду можно считать равной .
.
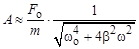 ;
;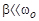 ), то
), то ,
, амплитуда вынужденных колебаний приблизительно равна
амплитуда вынужденных колебаний приблизительно равна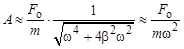 .
.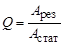 .
. .
.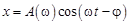 ,
, , т. е. ко-лебания осциллятора отстают по фазе от колебаний внешне-го воздействия F о×coswt.
, т. е. ко-лебания осциллятора отстают по фазе от колебаний внешне-го воздействия F о×coswt.
 , описывающему колебания некоторой точки волны.
, описывающему колебания некоторой точки волны. .
. ,
, ,
, ;
; ;
; .
. . Преобразовав это выражение получаем, что фазовая скорость может быть выражена через волновое число и циклическую частоту волны:
. Преобразовав это выражение получаем, что фазовая скорость может быть выражена через волновое число и циклическую частоту волны: .
. .
. .
. , можем записать
, можем записать .
. и деформация среды, вызванная колебаниями частиц
и деформация среды, вызванная колебаниями частиц  , неизменны.
, неизменны. ,
, ,
, .
.
 .
. ;
; ;
; .
.

 .
. .
. ,
, .
.
 .
.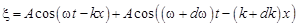 ,
, .
.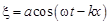 ,
,
 ,
, ,
, , т. е. «гребень» такой волны перемещается с фазовой скоростью.
, т. е. «гребень» такой волны перемещается с фазовой скоростью. и скорость
и скорость  . Это означает, что «гребень» перемещается со скоростью, отличной от v 1 и v 2.
. Это означает, что «гребень» перемещается со скоростью, отличной от v 1 и v 2. .
. . Поскольку производная от гармонической функции является гармонической функцией, постольку ток смещения также будет изменяться по гармони-ческому закону.
. Поскольку производная от гармонической функции является гармонической функцией, постольку ток смещения также будет изменяться по гармони-ческому закону. .
. Интеграл от гармонической функции также является гармо-нической функцией. Следовательно, маг-нитное поле, созданное током смещения, будет изменяться по гармоническому закону.
Интеграл от гармонической функции также является гармо-нической функцией. Следовательно, маг-нитное поле, созданное током смещения, будет изменяться по гармоническому закону. Это, в свою очередь, означает, что даже если исчезнет заряд, создавший изменяю-щееся электрическое поле, изменяющиеся электрическое и магнитное поля будут продолжать распространяться в прост-растве в виде электромагнитной волны.
Это, в свою очередь, означает, что даже если исчезнет заряд, создавший изменяю-щееся электрическое поле, изменяющиеся электрическое и магнитное поля будут продолжать распространяться в прост-растве в виде электромагнитной волны.

 ,
, .
.
 ,
, .
.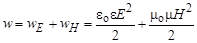 .
.
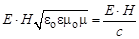
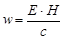 .
. . Это означает, что она показывает количество энергии, переносимой волной через единицу поверхности за единицу времени. Такую же размерность имеет плотность потока энергии.
. Это означает, что она показывает количество энергии, переносимой волной через единицу поверхности за единицу времени. Такую же размерность имеет плотность потока энергии. совпадает с направлением переноса энергии.
совпадает с направлением переноса энергии. представляет собой плотность потока энергии, переносимого электромагнитной волной в направлении её распространения. Этот вектор принято называть вектором Умова–Пойнтинга.
представляет собой плотность потока энергии, переносимого электромагнитной волной в направлении её распространения. Этот вектор принято называть вектором Умова–Пойнтинга.


