
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Стоячие волны. Колебания струныСодержание книги Поиск на нашем сайте
Пусть вдоль оси х навстречу друг другу распространяются две плоские гармонические волны с одинаковыми частотами и амплитудами:
Все частицы упругой среды, охваченной волновым про-цессом, будут участвовать в колебаниях, возбуждённых каждой из волн: x = x1 + x2 = Используя тригонометрическую формулу для суммы коси-нусов, получаем
где А (х) = 2Acos kx. Полученное выражение показывает, что частицы упругой среды, охваченные двумя волновыми процессами, совершают гармонические колебания с частотой w. Амплитуда колебаний частиц среды зависит от координаты х. В точках, координаты которых отвечают условию kx = ± n p, где n = 0, 1, 2, 3... cos kx = ±1 и амплитуда колебаний частиц среды максимальна. Такие точки называются пучностями. Координаты пучностей определяются соотношением В точках, отвечающих условию Поскольку амплитуда колебаний частиц среды определяется их координатой и не зависит от времени, постольку положение узлов и пучностей не изменяется. Узлы и пучности остаются на одном месте. Поэтому волну, возникающую в результате нало-жения встречных волн одинаковой частоты, называют стоячей. Рассмотрим натянутую струну, концы которой жёстко за-креплены. Пусть длина струны равна l. Допустим, что в этой струне возбуждены колебания. Струну можно представить себе как совокупность бесконечно малых связанных между собой элементов. Колебания одного такого элемента должны вовлекать в колебательный процесс и другие элементы струны. Следовательно, если в струне возбудить колебания, то в ней возникнет упругая волна. Конец струны жёстко закреплён, колебаться не может. Сле-довательно, он не может возбудить колебания в той среде, к ко-торой прикреплён. Поэтому волна, дошедшая до конца струны, полностью отразится. Это означает, что по струне будут распространяться две встречные волны Как показано выше, при наложении таких волн возникает стоячая волна. Это означает, что на струне с закреплёнными концами может возникнуть стоячая волна. Поскольку мы говорим о струне с жёстко закреплёнными концами, на концах струны всегда должна быть узлы. Из выражений для расчёта координат узлов и пучностей видно, что соседние узлы (так же как и пучности) отстоят друг от друга на l/2. Следовательно, длина струны должна быть такой, чтобы на ней целое число раз укладывалась половина длины волны:
где n = 1, 2, 3... Это, в свою очередь, означает, что на струне длинной l могут возникать стоячие волны лишь определённых частот
Эти частоты называются собственными частотами струны, или частотами нормальных колебаний. Колебания с такими частотами называют гармониками (колебание с частотой, соответствующей n = 1 называют первой гармоникой, n = 2 – второй гармоникой и т. д.).
Групповая скорость
В науке и технике волны широко используются для передачи информации. Однако гармоническая волна способна донести информацию лишь о том, что где-то есть источник волны. Для того чтобы с помощью волн можно было передавать необходимое количество информации, их необходимо изменять (например, испускать волны в виде импульсов, или изменять амплитуду волны, её частоту, начальную фазу). Такая волна называется модулированной. С помощью модулированных упругих волн определяют глубину морей и океанов (эхолот), а модулированные электро-магнитные волны позволяют осуществлять радио- и телевещание. Но если модулированные волны отличаются от гармони-ческих способностью переносить информацию, то, возможно, им присущи и другие отличия. Исследуем один из аспектов этой проблемы – найдём скорость, с которой модулированная волна переносит энергию. Для этого рассмотрим две одинаково направленные плоские поперечные бегущие волны, колебания которых происходят в одной плоскости, амплитуды которых равны, а частоты почти одинаковы. Тогда
Эту волну можно представить в виде
где
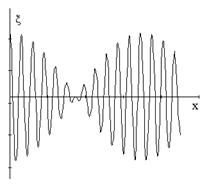
т. е. это волна с медленно изменяющейся амплиту-дой, или модулированная, такая же, как на рисунке. Показанная здесь кар-тина соответствует како-му-то моменту времени. В следующий момент она сдвинется вправо. Найдём скорость, с ко-торой модулированная волна будет распространяться. Для простоты рассмотрим точку, в которой амплитуда максимальна, – скорость перемещения этой точки равна скорости модулиро-ванной волны. Поведение точки с максимальной амплитудой описывается выражением Для любой бегущей волны
где v 1 и v 2 – фазовые скорость волн с циклическими частотами w1 и w2 соотвественно. Если дисперсии нет, то v 1 = v 2 = v и Если же среда диспергирующая, то Если вспомнить, что энергия колебаний пропорциональна квадрату амплитуды, то легко сообразить, что бóльшая часть энергии, переносимой такой волной, сконцентрирована там, где амплитуда волны велика. Это означает, что полученная скорость u есть скорость передачи энергии. Эту скорость u и называют групповой:
Важно отметить, что фронт волны распространяется с групповой скоростью.
Электромагнитные волны
К середине XIX в. был открыт ряд важнейших законов в области электричества и магнетизма. Значительная часть открытий в этой области принадлежит Майклу Фарадею. Этот крупнейший учёный, по праву считающийся осново-положником современной электродинамики, как это ни странно, не знал математики. Поэтому открытые им явления не имели математического описания. В 1854 г. в Кембриджский университет был принят на работу только что закончивший его Джеймс Клерк Максвелл. Основной целью своей деятельности он избрал математическое описание открытий Фарадея. Это ему удалось (см. разд. 5.6, 5.7). Один из результатов деятельности Максвелла – предсказание о существовании электромагнитных волн. Примерно через двадцать лет после этого электромагнитные волны были получены экспериментально немецким физиком Генрихом Герцем. Рассмотрим механизм возникновения и некоторые особенности электромагнитных волн. Допустим, что электрическое поле в вакууме создано зарядом, совершающим гармонические колебания. Электрическое поле, созданное таким зарядом, также должно изменяться с течением времени по гармоническому закону. Плотность тока смещения, созданного изменяющимся электрическим полем, равна Ток смещения создаёт магнитное поле
Важно отметить, что изменение электрического и магнитного полей опи-сывается одной и той же гармонической функцией. Ток смещения Вектор индукции магнитного поля всегда перпендикулярен создавшему его току. Это означает, что магнитное поле, созданное изменяющимся электрическим полем, будет перпендикулярно ему. В соответствии с уравнением Максвелла о циркуляции вектора Е, изменяющееся магнитное поле порождает электри-ческое. Причём порождаемое электрическое поле будет перпен-дикулярно изменяющемуся магнитному.
Более строгий анализ позволяет пока-зать, что изменяющиеся электрическое и магнитное поля описываются волновыми уравнениями:
где с – скорость света в вакууме (если электромагнитная волна распространяется в среде, то используется скорость света в этой среде). Решение этих уравнений имеет следующий вид:
где амплитуды Е и Н связаны соотношением
Можно также показать, что если вектор Е па-раллелен оси х, а вектор В параллелен оси у, то электромагнитная волна распро-страняется вдоль оси z (см. рису-нок). Другими словами, векторы Е, Н и вектор скорости электро-магнитной волны с образуют правую тройку. Важно отметить, что колеба-ния Е и Н синфазны.
|
||||||
|
Последнее изменение этой страницы: 2016-12-12; просмотров: 1139; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.41 (0.011 с.) |

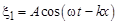 ,
, .
. +
+  .
. ,
, .
.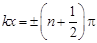 амплитуда равна нулю, т. е. частицы среды в этих точках не колеблются вообще. Такие точки называют узлами. Координаты узлов определяются соотношением
амплитуда равна нулю, т. е. частицы среды в этих точках не колеблются вообще. Такие точки называют узлами. Координаты узлов определяются соотношением  .
.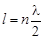 ,
,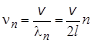 .
.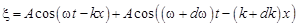 ,
, .
.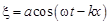 ,
,
 ,
, , и w= kv. Тогда скорость точки с максимальной амплитудой будет равна
, и w= kv. Тогда скорость точки с максимальной амплитудой будет равна ,
, , т. е. «гребень» такой волны перемещается с фазовой скоростью.
, т. е. «гребень» такой волны перемещается с фазовой скоростью. и скорость
и скорость  . Это означает, что «гребень» перемещается со скоростью, отличной от v 1 и v 2.
. Это означает, что «гребень» перемещается со скоростью, отличной от v 1 и v 2. .
. . Поскольку производная от гармонической функции является гармонической функцией, постольку ток смещения также будет изменяться по гармони-ческому закону.
. Поскольку производная от гармонической функции является гармонической функцией, постольку ток смещения также будет изменяться по гармони-ческому закону. .
. Интеграл от гармонической функции также является гармо-нической функцией. Следовательно, маг-нитное поле, созданное током смещения, будет изменяться по гармоническому закону.
Интеграл от гармонической функции также является гармо-нической функцией. Следовательно, маг-нитное поле, созданное током смещения, будет изменяться по гармоническому закону. Это, в свою очередь, означает, что даже если исчезнет заряд, создавший изменяю-щееся электрическое поле, изменяющиеся электрическое и магнитное поля будут продолжать распространяться в прост-растве в виде электромагнитной волны.
Это, в свою очередь, означает, что даже если исчезнет заряд, создавший изменяю-щееся электрическое поле, изменяющиеся электрическое и магнитное поля будут продолжать распространяться в прост-растве в виде электромагнитной волны.

 ,
, .
.



