
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вынужденные колебания пружинного маятникаСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
Рассмотрим поведение пружинного маятника, на который кроме силы трения действует внешняя сила, изменяющаяся по гармоническому закону: F = F о×cosw t. Уравнение движения для него в этом случае будет иметь вид
Введём коэффициенты
Получили неоднородное дифференциальное уравнение второ-го порядка. Общее решение такого уравнения является суммой общего решения однородного уравнения и частного решения неоднородного уравнения. Общее решение однородного уравнения уже было получено. Оно описывает затухающие колебания Для того чтобы найти частное решение неоднородного урав-нения, отметим следующее. В правой части уравнения стоит функция Следовательно, сумма слагаемых в левой части диффе-ренциального уравнения должна представлять собой такое же гармоническое колебание. Как показано в разд. 6.3.1 результатом сложения нескольких одинаково направленных гармонических колебаний с одина-ковыми частотами является гармоническое колебание. Поэтому каждый из членов суммы Допустим, что колебания х отстают по фазе от колебаний внешней силы на j: x = A cos(wt-j). Тогда слагаемое Взяв производную от х по времени и умножив её на 2b, получаем
Амплитуда А и начальная фаза j колебаний х являются неизвестными величинами. Для того чтобы найти выражения для расчёта этих величин, восполь-зуемся векторной формой пред-ставления гармонических коле-баний. В момент времени t = 0 фаза силы внешнего воздействия равна нулю, поэтому колебание Как уже отмечаось, Второй член суммы Первый член суммы Сумма этих векторов равна вектору Из векторной диаграммы на основе теоремы Пифагора получаем, что
Выражая отсюда А, получаем
Из векторной диаграммы также видно, что тангенс угла j равен
Таким образом, частное решение дифференциального уравне-ния имеет следующий вид:
Это выражение описывает установившиеся вынужденные колебания системы. Наличие в решении гармонической функции cos(w t -j), го-ворит о том, что под воздействием внешней гармонической силы осциллятор будет совершать гармоническое колебание с цикли-ческой частотой w, равной циклической частоте внешней вынуж-дающей силы. Амплитуда А и разность фаз j этих колебаний зависят от параметров осциллятора (wо, b) и от частоты внешнего воз-действия w. Как уже отмечалось, об-щее решение рассматривае-мого дифференциального уравнения равно сумме общего решения однородного уравнения и частного решения неоднородного
|
||
|
Последнее изменение этой страницы: 2016-12-12; просмотров: 993; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.156 (0.006 с.) |

 ,
, .
.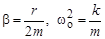 . Теперь дифферен-циальное уравнение принимает вид
. Теперь дифферен-циальное уравнение принимает вид .
. , где
, где  . Эти колебания возникают сразу после первого толчка внешней силы и по истечении некоторого времени затухают.
. Эти колебания возникают сразу после первого толчка внешней силы и по истечении некоторого времени затухают. , которая описывает гармоническое колебание с начальной фазой, равной нулю.
, которая описывает гармоническое колебание с начальной фазой, равной нулю. представляет собой гармоническое колебание, частота которого равна частоте внешнего воздействия w.
представляет собой гармоническое колебание, частота которого равна частоте внешнего воздействия w. можно записать следующим образом:
можно записать следующим образом:  .
. .
. Вторая производная от ко-ординаты маятника по времени равна
Вторая производная от ко-ординаты маятника по времени равна  .
.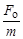 .
. , который расположен под углом -j относительно вектора
, который расположен под углом -j относительно вектора 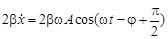 опережает по фазе
опережает по фазе  на p/2. Следовательно, вектор 2bwА распо-ложен под углом 90о относительно вектора
на p/2. Следовательно, вектор 2bwА распо-ложен под углом 90о относительно вектора 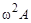 , который направлен против вектора
, который направлен против вектора  .
. .
. .
.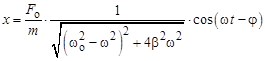 .
. уравнения, поэтому сразу после начала внешнего воз-действия колебания осцил-лятора будут представлять собой результат сложения двух колебаний – затухаю-щего с частотой w¢ и гар-монического с частотой внешнего воздействия w. По-степенно амплитуда зату-хающих колебаний становится пренебрежимо малой, а колебание – гармоническим (см. рисунок).
уравнения, поэтому сразу после начала внешнего воз-действия колебания осцил-лятора будут представлять собой результат сложения двух колебаний – затухаю-щего с частотой w¢ и гар-монического с частотой внешнего воздействия w. По-степенно амплитуда зату-хающих колебаний становится пренебрежимо малой, а колебание – гармоническим (см. рисунок).


