
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вынужденные колебания в колебательномСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
Контуре
В соответствии со вторым правилом Кирхгофа, сумма разностей потенциалов на элементах контура равна сумме эдс, дей-ствующих в рассматриваемом кон-туре. В рассматриваемом колебательном контуре два источника эдс – это источ-ник переменной эдс e и соленоид (в нём возникает эдс самоиндукции eL). На обкладках заряженного конденсатора имеется разность потенциалов. Обозначим её UC. Разность потенциалов на концах резистора, в соответствии с законом Ома, равна IR. Тогда уравнение, описывающее колебательный контур, имеет следующий вид:
Поскольку разность потенциалов на обкладках конденсатора
или
учитывая, что
и после деления на L
Вводя обозначения
Мы вновь получили неоднородное дифференциальное уравне-ние второго порядка. Полученное дифференциальное уравнение ничем не отличается от того, которое получено для пружинного маятника в предыдущем разделе. Следовательно, его решение имеет такой же вид: Это означает, что в колебательном контуре, содержащем источник переменной эдс, изменяющейся по гармоническому закону, будут происходить вынужденные колебания с частотой, равной частоте колебаний вынуждающей эдс.
Зависимость амплитуды вынужденных Колебаний от частоты внешнего воздействия. Явление резонанса
Рассмотрим зависимость амплитуды вынужденных колебаний от частоты внешнего воздействия и параметров осциллятора более подробно. Из выражения амплитуда вынужденных колебаний зависит от частоты внешнего воздействия w. Можно показать, что эта функция имеет экстремум, т. е. при определённой частоте амплитуда вынуж-денных колебаний будет максимальной. Это явление называют резонансом, а частоту вынужденных колебаний, при которой амплитуда максимальна – резонансной частотой. При резонансной частоте амплитуда максимальна, а знаменатель выражения, показывающего величину амплитуды, минимален. Найдём эту частоту. Знаменатель имеет экстремум при частоте внешнего воздействия, на которой производная от знаменателя по частоте w равна нулю:
Полученное выражение будет равно нулю при двух значениях частоты внешнего воздействия: w = 0 и Если w = 0, то колебаний нет, поэтому первый корень уравнения отбрасываем. Второй же корень и есть резонансная частота wрез. Именно при частоте внешнего воздействия
При слабом затухании (
Обратите внимание на то, что значение b достаточно сильно влияет на амплитуду при резо-нансе (см. рисунок): чем больше потери, тем меньше резонансная амплитуда. При отклонении частоты внешнего воздействия от резо-нансной амплитуда вынужден-ных колебаний уменьшается (см. рисунок). Теперь найдём амплитуду вынужденных колебаний для низких (w<<wо) и высоких (w>>wо) частот внешнего воз-действия. При w<<wо амплитуда вы-нужденных колебаний будет приблизительно равна:
если затухание мало (
где k – коэффициент упругости пружины. В полученном выражении отсутствует частота внешнего воздействия. Это значит, что при малых частотах внешнего воздействия колебательная система реагирует на гармоническую внешнюю силу практически как на статическую, т. е. не изменяющуюся с течением времени. Амплитуда вынужденных колебаний определяется величиной внешнего воздействия и упругими свойствами осциллятора. При высоких частотах (w>>wо). и при
Таким образом, при высокой частоте внешнего воздействия максимальное отклонение от положения равновесия А опре-деляется величиной внешнего воздействия, инертностью осцил-лятора и частотой воздействия. Упругие свойства колебательной системы не имеют никакого значения (поскольку в выражении отсутствует wо).
Добротность
Добротность используется для характеристики колебательных систем. Добротность определяют как отношение амплитуды вынуж-денных колебаний при резонансе А рез к амплитуде при низкой частоте А стат
Используя полученные в разд. 8.3 выражения для А рез и А стат, получаем
Добротность показывает, во сколько раз амплитуда при резонансе больше амплитуды вынужденных колебаний при низких частотах.
Следовательно, чем больше добротность, тем сильнее проявляет себя резонанс при вынужденных колебаниях. Можно сказать и иначе: чем меньше потери энергии, тем сильнее резонанс.
|
|||||||
|
Последнее изменение этой страницы: 2016-12-12; просмотров: 441; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.142.210.41 (0.01 с.) |

 Рассмотрим электрическую цепь, содержащую соленоид, кон-денсатор, резистор и источник переменной эдс, изменяющейся по гармоническому закону
Рассмотрим электрическую цепь, содержащую соленоид, кон-денсатор, резистор и источник переменной эдс, изменяющейся по гармоническому закону  .
.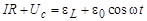 .
. , а эдс самоиндукции
, а эдс самоиндукции 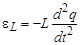 ,
,
 ;
; , получаем
, получаем
 .
. и
и  , получаем
, получаем .
. .
. видно, что
видно, что .
. .
. амплитуда вынужденных колебаний максимальна. Её значение
амплитуда вынужденных колебаний максимальна. Её значение
 .
. ) резонансную амплитуду можно считать равной
) резонансную амплитуду можно считать равной .
.
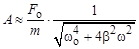 ;
;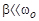 ), то
), то ,
, амплитуда вынужденных колебаний приблизительно равна
амплитуда вынужденных колебаний приблизительно равна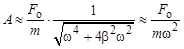 .
.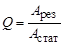 .
. .
.


