
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Уравнение плоской гармонической волныСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
Рассмотрим ряд точек плоской волны, лежащих на прямой, проходящей через источник колебаний. Поскольку волна гармоническая, все точки колеблются по закону x= Поскольку точки, расположенные дальше от источника, начали колебаться позже, их колебания отстают по фазе от колебаний источника. Найдём величину этого сдвига по фазе a. Если точка находится на расстоянии х от источника, то колебания «доберутся» до неё через Поскольку отставание по фазе a обусловлено задержкой начала колебаний точки на t секунд, это уравнение можно записать в виде
где Таким образом, колебания произвольной точки, находящейся на расстоянии х от источника, описывается уравнением
Как видно из этого уравнения, смещение x интересующей нас точки меняется по гармоническому закону. Фаза гармонической функции зависит от t и от х. Произвольная точка среды, расположенная на расстоянии х от источника, колеблется по закону
где a = - kx.
___________________________
* Символ x читается как «кси». Положение всех вовлечённых в волновой процесс точек среды в момент времени t определяется выражением
где Таким образом, смещение вовлечённых в волновой процесс точек среды зависит от координаты точки. Обе функции периодические. Но первая периодична во времени t, а вторая – по координате х. В свою очередь функция
Пространственный период называется длиной волны l. Выразим длину волны через другие параметры волнового процесса. За один период гармоничес-кой функции ее фаза и меняется на 2p, поэтому
Учитывая, что
(v – скорость распространения колебаний в пространстве; n – частота волны; Т – период волны). Из последнего выражения следует, что длина волны есть расстояние, которое волна проходит за один период. Волновое число, которое было введено как отношение циклической частоты к скорости волны, можно выразить и через длину волны (из выражения
Физический смысл волнового числа можно определить следующим образом. Найдём производную от фазы волны по х *.
Таким образом, волновое число k есть скорость изменения фазы колебаний по координате.
Фазовая скорость
Вернёмся к уравнению Выделим из него фазу
Пусть фаза имеет фиксированное значение, т. е. j = con st. Тогда
или
т. е. фазу, которую в момент t имела частица среды, находящаяся на расстоянии х от источника волны, через dt секунд будет иметь частица, находящаяся на dx метров дальше. Другими словами, любое постоянное значение фазы перемещается, удаляясь от источника. Сокращая w в последнем выражении, получаем
______________________________
* Физический смысл производной – скорость изменения функции по изменению ее аргумента.
Таким образом скорость v является скоростью, с которой перемещается фиксированное значение фазы. Поэтому её называют фазовой скоростью. Волновое число k по определению равно
Отметим ещё одну деталь. Величина отношения w/ k зависит от значения частоты, поэтому фазовая скорость волн разных частот будет разной. Такое явление действительно существует и называется дисперсией волн. Среды, в которых имеет место дисперсия, называют диспергирующими.
Волновое уравнение
Волновым называют дифференциальное уравнение, описы-вающее процесс распространения гармонических волн в среде. Найдём вид этого уравнения в простейшем случае – для плоской бегущей волны, распространяющейся параллельно оси х,
Возьмём вторые производные от x по времени и координате:
Учитывая, что
Таким образом, если анализ некоторой системы приводит нас к дифференциальному уравнению Уравнение волны Обратите внимание: волновое уравнение не следует путать с уравнением волны. Волновое уравнение описывает процесс распространения гармонических колебаний в некоторой среде. Уравнение волны показывает, как смещены от положения равновесия частицы упругой среды в зависимости от t и х.
Энергия упругой волны
Пусть вдоль оси х распространяется плоская волна
Выделим некоторый малый объём D V в пределах которого скорость движения колеблющихся частиц Тогда кинетическая энергия частиц в этом объёме
где r – плотность упругой среды. Можно показать, что потенциальная энергия упругой деформации этого объёма
где v – фазовая скорость волны.
Полная энергия равна сумме кинетической и потенциальной энергий:
Объёмная плотность энергии, равная энергии единичного объёма
Поскольку
и
Так как
и, наконец,
Как известно, среднее значение квадрата синуса равно 1/2. Следовательно, среднее значение плотности энергии
Отсюда видно, что среднее значение плотности энергии зависит от плотности среды, амплитуды колебаний и цикли-ческой частоты волны. Вообще же плотность энергии волны различна в разные моменты времени в одной точке пространства и в один момент времени в разных точках пространства. Эта энергия испускается источником колебаний и переносится волной в пространстве. Кроме объёмной плотности энергии используется плотность потока энергии j, которая равна энергии, перенесённой волной через единичную поверхность D Sn, перпендикулярную направ-лению распространения волны, за единицу времени. В аналитической форме определение плотности потока энергии имеет вид
где D Е – энергия, переносимая за время D t через площадку D Sn, перпендикулярную к скорости распространения волны. В случае плоской волны
Тогда
или, векторной форме,
Вектор j называют вектором Умова. Этот вектор показывает, какая энергия передаётся волной за единицу времени через единицу площади и в каком направлении она распространяется. Как видите, направление переноса энергии определяется ско-ростью волны – энергия переносится волной в направлении распространения волны.
|
||
|
Последнее изменение этой страницы: 2016-12-12; просмотров: 1805; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.156 (0.007 с.) |

 *.
*. секунд после начала колебаний источника (v – скорость распространения волны).
секунд после начала колебаний источника (v – скорость распространения волны).

 ,
, – волновое число.
– волновое число. .
. ,
, ,
,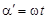 .
.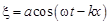 имеет временнýю и пространственную периодичность.
имеет временнýю и пространственную периодичность. Периодичность во времени характеризуется периодом Т – временем, за которое совер-шается одно колебание частицы среды.
Периодичность во времени характеризуется периодом Т – временем, за которое совер-шается одно колебание частицы среды.
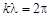 ;
; .
. ;
; .
.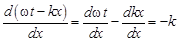 .
. , описывающему колебания некоторой точки волны.
, описывающему колебания некоторой точки волны. .
. ,
, ,
, ;
; ;
; .
. .
. .
. , можем записать
, можем записать .
. и деформация среды, вызванная колебаниями частиц
и деформация среды, вызванная колебаниями частиц  , неизменны.
, неизменны. ,
, ,
, .
.
 .
. ;
; ;
; .
.

 .
. .
. ,
, .
.
 .
.


