
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Энергия при гармоническом колебательном движенииСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
В момент наибольшего смещения скорость тела равняется нулю, и вся его энергия переходит в потенциальную. При прохождении телом положения равновесия скорость его максимальна и вся энергия переходит в кинетическую.
10. сложение гармонических колебаний,происходящих по одной прямой.сложение взаимно перпендикулярных колебаний.сложное колебание и его гармонический спектр. Рассмотрим вращающийся против часовой стрелки с постоянной угловой скоростью w вектор А. Очевидно, что угол j = w t + j0 где j0 - начальный угол. Проекции вектора А на оси координат запишутся:
Видно, что проекции вращающегося вектора на оси координат по форме совпадают с уравнением гармонических колебаний, если угловой скорости вектора сопоставить угловую частоту колебаний, а начальному углу - начальную фазу. Проводя аналогию дальше, можно сказать, что результат сложения двух однонаправленных колебаний можно получить следующим путем: необходимо сложить два вектора, а проекции суммарного вектора на оси координат будут являться уравнениями результирующего колебания. Рассмотрим этот метод на примере сложения двух колебаний с произвольными частотами. Пусть наше тело участвует в двух совпадающих по направлению колебаниях:
Сопоставим этим колебаниям два вектора А1 и А2, вращающихся с соответствующими угловыми скоростями.
Сопоставляем колебаниям проекции векторов на ось y. Задача сложения колебаний сводится к нахождению проекции вектора А на ось y (амплитуда результирующего колебания) и угла f (фаза результирующего колебания). Из очевидных геометрических соображений находим:
Отметим, что в общем случае сложения колебаний с разными частотами амплитуда результирующего колебания будет зависеть от времени. Если же частоты одинаковы, то
Рассмотрим сложение двух однонаправленных колебаний с неравными, но близкими частотами, то есть
получим уравнение суммарного колебания:
Полученное результирующее колебание не является гармоническим (сравни с уравнением (1)); такого вида колебания носят название биений, название понятно, если посмотреть на график колебаний.
посмотреть на осциллографе Величина, стоящая перед синусом, меняется со временем относительно медленно, так как разность частот мала. Эту величину условно называют амплитудой биений, а разность складываемых частот При сложении взаимно перпендикулярных колебаний необходимо найти уравнение траектории тела, то есть из уравнений колебаний типа x = x(t), y = y(t) исключить t и получить зависимость типа y(x). например, сложим два колебания с одинаковыми частотами:
исключив время, получим:
В общем случае это - уравнение эллипса. При A1=A2 - окружность, при Вид траектории при сложении взаимно перпендикулярных колебаний зависит от соотношения амплитуд, частот и начальных фаз складываемых колебаний. Получающиеся кривые носят название фигур Лиссажу. Совокупность гармонических колебаний (гармоник), на которые разложено сложное колебание, называется гармоническим спектром сложного колебания. Гармонический спектр удобно представить как набор частот (или круговых частот) отдельных гармоник совместно с соответствующими им амплитудами.
11. свободные колебания.затухающие колебания.логарифмический декремент затухания.вынужденные колебания.уравнение вынужденных колебаний.резонанс. Свободными колебаниями называют такие, которые совершаются без внешних воздействий за счет первоначально полученной телом энергии. В реальных условиях любая механическая система находится под действием сил трения. При этом часть механической энергии превращается во внутреннюю энергию теплового движения, и свободные колебания становятся затухающими. Уравнение затухающих колебаний
Изменение амплитуды:
Быстрота убывания амплитуды колебаний определяется коэффициентом затухания: чем сильнее тормозящее действие среды, тем больше β и тем быстрее уменьшается амплитуда. Быстроту затухания часто характеризуют логарифмическим декрементом затухания λ - величиной, равной натуральному логарифму отношения двух последовательных амплитуд, разделенных интервалом времени, равным периоду колебаний:
Коэффициент затухания и логарифмический декремент затухания связаны простой зависимостью: λ = βТ. Вынужденные колебания – колебания, возникающие под действием внешней периодически изменяющейся силы. Частота вынужденных колебаний равна частоте изменения внешней силы. Если частота ν внешней силы совпадет с частотой ν0 свободных колебаний системы, то амплитуда колебаний резко возрастает. Это явление называется резонансом. Наиболее простой и содержательный пример вынужденных колебаний можно получить из рассмотрения гармонического осциллятора и вынуждающей силы, которая изменяется по закону:
12. волны в упругой среде.образование волн.основные параметры волны:фаза,длина,фронт,скорость распространения влны.Уравнение волны,её график.поток энергии волны.вектор Умова. Если в каком-либо месте упругой (твердой, жидкой или газообразной) среды возбудить колебания ее частиц, то вследствие взаимодействия между частицами это колебание начнет распространяться в среде с некоторой скоростью v. Процесс распространения колебаний называется волной. Частицы среды, в которой распространяется волна, не переносятся волной, они лишь совершают колебания около своих положений равновесия. В зависимости от направления колебания частиц по отношению к направлению, в котором распространяется волна, различают продольные и поперечные волны. В продольной волне частицы среды колеблются вдоль направления распространения волны. В поперечной волне частицы среды колеблются в направлениях, перпендикулярных к направлению распространения волны. Механические поперечные волны могут возникнуть лишь в среде, обладающей сопротивлением сдвигу. Поэтому в жидкой и газообразной средах возможно возникновение только продольных волн. В твердой среде возможно возникновение как продольных, так и поперечных волн. В продольных волнах вследствие совпадения направлений колебаний частиц и волны появляются сгущения и разрежения.
Скорость волны определяется скоростью распространения колебаний от одной точки среды к другой:
Скорость продольных волн определяется по формуле: где ρ- плотность среды, E - модуль Юнга, G - модуль сдвига.
j=w*v 13. Акустика.Тоны,шумы,звуковые удары.физические характеристики звука.интенсивность и уровень интенсивности звука.звуковое давление.единица шкалы уровней интенсивностей звука. Акустика – область физики, исследующая упругие колебания и волны от самых низких частот до предельно высоких (10-12 – 1013 Гц), воспринимаемых человеческим ухом. Звук – механические волны, распространяющиеся в упругой среде – в газах, жидкостях, твердых телах. Ухо человека воспринимает звук, частоты которого лежат в пределах от 16 Гц до 20 кГц. Пограничные со звуком области получили название: инфразвук (частота ниже 16 Гц) и ультразвук (частота выше 20 кГц). Принято различать следующие звуки: 1) тоны, или музыкальные звуки; 2) шумы; 3) звуковые удары. Тон - звук, являющийся периодическим процессом. Если процесс гармонический, то тон называется простым или чистым. Простой тон издает, например, камертон, сложный издается музыкальными инструментами, аппаратом речи. Шум - звук, отличающийся сложной неповторяющейся временной зависимостью (звуки от вибрации машин, аплодисменты, шорох). Звуковой удар – кратковременное звуковое воздействие: хлопок.
|
||||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 419; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.10.75 (0.007 с.) |





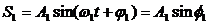




 , то есть зависимость от времени исчезает. На языке векторной диаграммы это означает, что складываемые векторы при своем вращении не меняют своего относительного положения. В этом случае формулы для амплитуды и фазы результирующего колебания запишутся так:
, то есть зависимость от времени исчезает. На языке векторной диаграммы это означает, что складываемые векторы при своем вращении не меняют своего относительного положения. В этом случае формулы для амплитуды и фазы результирующего колебания запишутся так: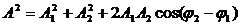


 , и пусть для определенности
, и пусть для определенности  . Для простоты пусть начальные фазы и амплитуды этих колебаний равны. В результате сложения двух колебаний
. Для простоты пусть начальные фазы и амплитуды этих колебаний равны. В результате сложения двух колебаний



 - частотой биений (циклической).
- частотой биений (циклической).


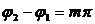 (m - целое) - отрезок прямой.
(m - целое) - отрезок прямой.

 .
.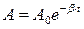 , где А0 - амплитуда в момент t = 0.
, где А0 - амплитуда в момент t = 0.

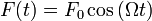 .
. Эффект резонанса для разных частот внешнего воздействия и коэффициентов затухания
Эффект резонанса для разных частот внешнего воздействия и коэффициентов затухания
 Так как
Так как  то,
то,
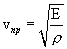 , а поперечной:
, а поперечной: 



