
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Интенсивность выделения энергииСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте Энергетический критерий разрушения Гриффитса [1, 2] гласит рост трещины может иметь место в том случае, если система может выделить энергию, необходимую для образования дополнительной трещины с размером da. В гл. I был рассмотрен случай пластины с неподвижными краями. В этом случае внешняя нагрузка не может совершить никакой работы. Поэтому энергия, необходимая для роста трещины, должна быть передана за счет освобождения упругой энергии. Если края пластины во время расширения трещины могут свободно перемещаться, то внешняя нагрузка совершает работу. В этом случае упругая энергия, накопленная в пластине, не· уменьшается, а увеличивается. Для пластины единичной толщины условие роста трещины можно записать в виде
где U — содержащаяся в пластине упругая энергия; F — работа, совершаемая внешней силой; W —энергия, необходимая для образования трещины. По аналогии с гл. I, G;= d(F — U)/da есть «интенсивность выделения энергии», или «сила раскрытия трещины», a R;= = dW/'da —■ сопротивление росту трещины. Рассмотрим пластину толщины В, на которую действует нагрузка Р, как показано на рис. 5.1 Под действием нагрузки точки приложения силы перемещаются относительно друг друга на расстояние v. При увеличении размера трещины на da это относительное перемеще
запасенная в пластине толщины В. Деформации считаем упругими. В отсутствие роста трещины перемещение ν пропорционально нагрузке: v^=CP, где С —податливость пластины (величина, обратная ее жесткости). Для пластины без трещины, имеющей длину L, ширину W и толщину В, податливость С ~ = L/(WBE), где Ε —модуль Юнга. Упругая энергия, заключенная в пластине (с трещиной), Ut = Pv/2 = CP2/2. (5.3) Используя уравнение (5.3), можно вычислить величину, определяемую выражением (5.2), откуда получим (см. [3, 4])
Члены с dP/da сокращаются. Это означает, что величина G не зависит от того, является нагрузка постоянной или нет:
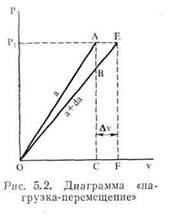
Величина G всегда равна производной от упругой энергии (однако знак этой величины при различных условиях" нагружения различен: при постоянной нагрузке U увеличивается, а при неподвижных зажимах U уменьшается). Величину G можно также получить графически. Для трещины размера а (упругая) диаграмма «нагрузка —перемещение» представлена на рис. 5.2 линией О А. Для трещины длиной а + da соотношение между нагрузкой и перемещением представлено линией ОЕ. Пусть увеличение размера трещины от а до а + da происходит при нагрузке /V Если края пластины остаются неподвижными, то перемещение остается постоянным, а нагрузка уменьшается по линии АВ. Это означает, что выделение упругой энергии представлено треугольником ОАВ. Если расширение трещины происходит при постоянной нагрузке,то происходит относительное перемещение ее краев на величину Αν. Совершенная нагрузкой работа есть ΡΑν, что равно площади AEFC. Заключенная в пластине упругая энергия увеличивается при этом от ОАС до OEF. Прирост этой энергии равен площади треугольника ОАЕ. Эта энергия должна быть равна работе, совершенной нагрузкой. Поскольку площадь, очерченная фигурой AEFC, вдвое превосходит площадь треугольника ОАЕ, остается энергия, равная площади ОАЕ.
Пренебрегая маленьким треугольником ЛЕВ, получаем, что ОЛВ s=;= ОЛЕ. Это означает, что в обоих случаях для роста трещины высвобождается одинаковая энергия. В случае неподвижных зажимов энергия высвобождается за счет уменьшения упругой энергии пластины. При постоянной нагрузке источником этой энергии является работа внешней нагрузки. В обоих случаях результаты одинаковы, и поэтому величину G можно вычислить, зная закон изменения упругой энергии. По этой причине величину G называют интенсивностью выделения упругой энергии. Поскольку G есть интенсивность выделения упругой энергии, она должна быть пропорциональна σ2/Ε. Эта величина равна энергии, приходящейся на единицу распространения трещины, следовательно, она должна быть равна энергии пластины, деленной на ее длину и на толщину (G есть величина, приходящаяся на единицу толщины). Поэтому величина G пропорциональна длине:
где С —константа, а λ —характерная длина. В бесконечной пластине с краевой трещиной длины а или с центральной трещиной длины 2а единственным характерным размером является величина а. Для одной вершины трещины С?= π. Индекс I при G означает разрывающий тип нагрузки. Из уравнения (5.6) следует, что для плоского напряженного состояния Gi i=a Κι/Ε. Это соотношение можно получить и иным Из рис. 5.3 следует, что
Необходимость коэффициента 2 определяется тем, что в трещине есть верхний и нижний края. Двойка в знаменателе учитывает тот факт, что напряжения увеличиваются от нуля.
Если начало системы координат лежит в центре трещины, то из гл. III следует, что Полагая в соотношении (5.11) г/Ь f= sin2q), получаем: G = К\1е (плоское напряженное состояние); ·. _ G\ = (1 — v2)/Cf/£ (плоская деформация). J Аналогично можно показать, что для трещин типов II и III
Суммарную интенсивность выделения энергии при распространении трещин смешанного типа легко получить, складывая эти величины для различных типов трещин:
Критерий роста трещины Увеличение длины трещины происходит тогда, когда величина G равна энергии, необходимой для роста трещины. В истинно хрупких материалах, например таких, как стекло, энергией, оказывающей влияние на рост трещины, является поверхностная энергия, необходимая для образования новых свободных поверхностей, т. е.
Уравнение (5.1) можно разрешить с помощью уравнений (5.6) и (5.15), откуда получаем:
что и является критерием Гриффитса [1, 2]. Ирвин [6] и Орован [7] заметили, что энергия, необходимая для роста трещины в металле, намного превосходит поверхностную энергию, необходимую для обра-
зования новых свободных поверхностей. В металлах перед трещиной образуются пластические деформации, и во время распространения трещины энергия расходуется на образование зоны пластичности при вершине распространяющейся трещины. Если пластическая энергия R для одинаковых приращений размеров различных трещин одинакова, то величина R p=s dWIda остается постоянной. Из эксперимента следует, что это приблизительно верно для трещин, распространяющихся при плоской деформации: образцы с трещина-- ми различных размеров, как оказывается, разрушаются при одних и тех же значениях G. Это критическое значение G обозначают как Gk;= (1 -v*)Kl/E. Следовательно, в случае плоской деформации R р= dWIda — G\c, откуда следует, что
Критерий разрушения можно изобразить графически так, как показано на рис. 5.4. Сопротивление росту трещины R не зависит
При заданном напряжении ai скорость выделения энергии пропорциональна размеру трещины а. Для этого случая величина G представлена на рисунке линией О А. Если трещина имеет размер оь то скорость выделения энергии при напряжении σ2 представлена точ-
кой В. При увеличении напряжения от σ2 до at величина G увеличивается от точки В до точки А. В точке А может произойти увеличение размера трещины, так как выполняется условие G >= R. В более длинной трещине размера а2 эта ситуация возникает уже при напряжении σ2 (точка С). Более универсальное представление критерия разрушения приведено на рис. 5.5. Вправо отложена величина приращения длины трещины Δα, а влево —начальный размер трещины аг Как и прежде, величина G представлена прямыми линиями, например при напряжении σ2 величина G задана линией LF. Из всех точек линии LF реальную ситуацию описывает только точка F, поскольку с самого начала размер трещины равен а1. При возрастании нагрузки на трещину от нуля до σ2 соответствующая ей величина G возрастает от 0 до F. Дальнейшее увеличение напряжения до величины а{ приводит к увеличению G до точки Н. После этого происходит разрушение. Расширение трещины при напряжении а1 приводит к изменению G вдоль линии FIK, и, следовательно, G остается большим, чем R. Если нагрузка на трещину размера а2 возрастает от нуля до σ2, то соответствующее ей значение G увеличивается от 0 до Я (обратите внимание на то, что линии LF и МН параллельны). В точке Η происходит увеличение длины трещины: если напряжение остается равным σ2, то скорость выделения энергии изменяется вдоль линии ΗΝ и G остается большим, чем R. В § 5.1 было показано, что в обоих случаях роста трещины при постоянном напряжении и при фиксированных захватах величина G имеет одно и то же значение. Однако это имеет место только ι начале процесса увеличения длины трещины. В процессе роста трещины это условие не выполняется. Если распространение трещины происходит при постоянном напряжении, то G меняется вдоль прямых линий, как показано на рис. 5.5. Если рост трещины происходит при неподвижных захватах, то напряжение уменьшается. Поскольку
но а, а медленнее (рис. 5.6). При определенной геометрии образца, если рост трещины происходит при неподвижных захватах, G может даже уменьшиться. Обсуждению этой задачи, а также вытекающих отсюда следствий посвящена гл. VI.
|
||||||||||||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 636; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.156 (0.011 с.) |

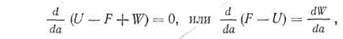
 увеличивается на dv. Следовательно, совершенная внешними силами работа будет равна Pdv. Отсюда следует, что
увеличивается на dv. Следовательно, совершенная внешними силами работа будет равна Pdv. Отсюда следует, что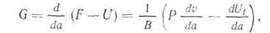
 где В —толщина пластины [отметим, что уравнение (5.1) записано для пластины единичной толщины], a U, — полная упругая энергия.
где В —толщина пластины [отметим, что уравнение (5.1) записано для пластины единичной толщины], a U, — полная упругая энергия.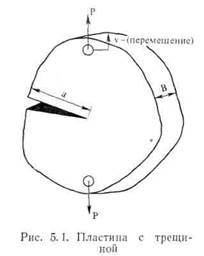
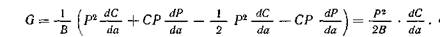

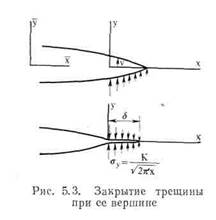
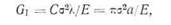
 путем. Рассмотрим бесконечную пластину с неподвижными краями! содержащую трещину длины а. Силы, приложенные к краям трещины (рис. 5.3) и достаточные для того, чтобы закрыть трещину на бесконечно малом расстоянии 8, совершат определенную работу. Эта работа равна энергии, выделяемой при расцеплении краев трещины (см. [5]).
путем. Рассмотрим бесконечную пластину с неподвижными краями! содержащую трещину длины а. Силы, приложенные к краям трещины (рис. 5.3) и достаточные для того, чтобы закрыть трещину на бесконечно малом расстоянии 8, совершат определенную работу. Эта работа равна энергии, выделяемой при расцеплении краев трещины (см. [5]).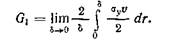
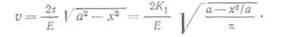
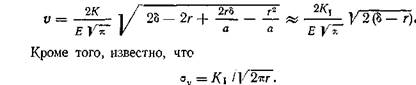
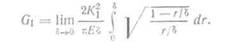
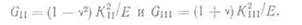
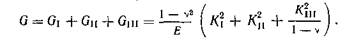 Используя уравнения (5.12) и применяя корректировочные коэффициенты для К, учитывающие конечность размеров (см. гл. III), можно определить величину G для пластин с конечными размерами.
Используя уравнения (5.12) и применяя корректировочные коэффициенты для К, учитывающие конечность размеров (см. гл. III), можно определить величину G для пластин с конечными размерами.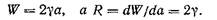
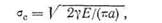


 от размера трещины; поэтому эта величина представлена на рисунке прямой горизонтальной линией R τ= G\c. Интенсивность выделения энергии
от размера трещины; поэтому эта величина представлена на рисунке прямой горизонтальной линией R τ= G\c. Интенсивность выделения энергии (5.18)
(5.18)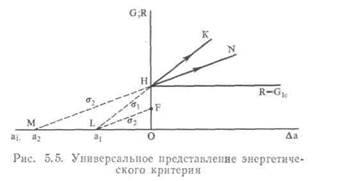
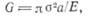 то отсюда следует, что величина G увеличивается не пропорциональ-
то отсюда следует, что величина G увеличивается не пропорциональ-



