
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Сопротивление росту трещины (R-кривая)Содержание книги Поиск на нашем сайте
До сих пор величина R рассматривалась как не зависящая от длины трещины. Это приблизительно верно для трещин, находящихся в плоском деформированном состоянии. В случае плоского напряженного состояния сопротивление росту трещины, как было показано в экспериментах, изменяется. Рассмотрим трещину в листе, достаточно тонком для того, чтобы в нем возникло плоское напряженное состояние (см. гл. VII и VIII). Когда образец нагружен до напряжения σ;, начинается процесс распространения трещины. Однако процесс роста трещины пока стабилен и разрушение еще не наступает. Если напряжение остается равным σ., то трещина распространяется только на небольшое расстояние и останавливается. Для поддержания процесса роста трещины необходимо дальнейшее увеличение напряжения: несмотря на то что трещина стала длиннее, она может выдержать большие напряжения. Процесс одновременного увеличения размера трещины и напряжения может быть продолжен, пока при напряжении ас не В начале процесса роста трещины должен выполняться энергетический критерий. При стабильном росте трещины скорость выделения энергии в точности равна сопротивлению росту трещины (если она меньше, то трещина прекращает расти, если больше, то возни-
кает нестабильность, предшествующая разрушению). Скорость выделения энергии G = π σ2αίΕ, и во время роста трещины увеличивается как σ, так и а. Это означает, что G увеличивается не пропорционально а, а быстрее. Так как G ¢= R, то отсюда следует заключить, что R увеличивается так, как показано графически на рис. 5.8. Пусть трещина размера а. нагружена до напряжения α ι. Если бы трещина росла, то количество выделяемой при этом энергии было бы задано точкой А. Однако эта вели-
Пусть это значение достаточно для роста трещины. Если бы трещина распространялась при постоянном напряжении, то величина G увеличивалась бы по линии ВН. Эта линия лежит ниже ^-кривой, и поэтому при постоянном напряжении трещина расти не может.
Дальнейшее увеличение напряжения до величины σ2 приводит к увеличению размера трещины на Аа2. Величины G и R изменяются вдоль ^-кривой от β к С. Наконец, при напряжении ос длина трещины становится равной ас, а величины G и R доходят до точки D. Рост трещины при постоянном напряжении ас сопровождается увеличением G по линии DF. Эта линия лежит выше ^-кривой. Поскольку G остается большим, чем R, происходит окончательное разрушение в точке D, в которой
Уравнение (5.19), очевидно, представляет собой энергетический критерий для разрушения при плоском напряженном состоянии. Количественная оценка этого критерия разрушения возможна, если будет получено аналитическое выражение для ^-кривой. Попытки вывода этого выражения были сделаны в работах [8—11]. Оценка критерия разрушения проведена в гл. VIII. Крафт и др. [12] сделали предположение, что ^-кривая инвариантна: она имеет одинаковый вид безотносительно к начальному размеру трещины. Это означает, что условие разрушения для трещин произвольных размеров следует из графического построения, которое выполнено на рис. 5.9, где касательные для различных длин трещин проведены к единственной /^-кривой. 7?-кривая представляет собой энергию, необходимую для роста трещины. В вязком материале эта энергия слагается из работы, необходимой для образования новой зоны пластичности при вершине развивающейся трещины, и работы, необходимой для образования,
роста и слияния микропустот. Наиболее вероятно, что последняя мала по сравнению с энергией, содержащейся в зоне пластичности. Поэтому ^-кривая должна начинаться в нулевой точке, как показано на рис. 5.9: при нулевых напряжениях размер зоны пластичности равен нулю. Это также означает, что при любом напряжении, отличном от нуля, выполняется энергетический критерий (не считая работы образования пустот). Однако трещина не растет, поскольку напряжения и пластические деформации все еще недостаточны. Энергетический критерий является критерием необходимым, но недостаточным. Материал при вершине трещины не будет готов к расцеплению, пока напряжения и деформации не станут достаточно велики, чтобы стало возможно образование и слияние пустот. К моменту, когда возникает такая ситуация, образуется довольно большая зона пластичности. Трещина может расти только в том случае, если в процессе ее роста выделяется достаточно энергии, чтобы совершить работу по образованию зоны пластичности при новой вершине трещины. Трещина не может расти, если не удовлетворено это энергетическое условие; она должна расти, если это условие удовлетворено.
Легко видеть, что все линии роста трещин пересекаются в точке В (рис. 5.9). Эта точка является общей для трещин с размерами ал и а2, поэтому
Стабильный рост трещины начинается при определенном значении G, а именно при G;, заданном уравнением (5.20). При G, равном G., рост трещины происходит от точки В до точки Ci или С2, где G?= R. Это первое отдельное расширение трещины называется хлопком, потому что представляет собой внезапное метастабильное расширение трещины, которое часто сопровождается звучным щелчком. После хлопка происходит непрерывный стабильный медленный рост трещины, пока в точке D± или D2 не последует разрушение. Для двух рассматриваемых трещин значения G равны соответственно Glcl и Gic2. Это означает, что критическая скорость выделения энергии для плоского напряженного состояния Gic не является постоянной величиной и, поскольку К2и = EGic, отсюда величина Kic также непостоянна (индекс 1 используется здесь для обозначения плоского напряженного состояния в трещине типа I, чтобы отличать Ки и Glc от значений К\с и G\c при плоской деформации). В отличие от случая плоской деформации, когда G\c и К\с в определенных пределах являются константами материала, величины Gic и Kic зависят от размера трещины и для больших трещин имеют большие значения. В § 5.1 было отмечено, что с помощью соотношения К21 = EGi к величине G можно применить коррекцию на конечность размеров. Используя при этом коррекцию Ирвина [3] (см. гл. III), получим
Уравнение (5.21) означает, что линии G —не прямые, а имеют положительную кривизну, как показано на рис. 5.10. Для маленькой трещины коррекцией на конечность размеров можно пренебречь и считать линию G приблизительно прямой. По мере удлинения трещин увеличивается и кривизна. В результате значение Glc сначала уве-
личивается от Gici до Gic2, а затем вновь уменьшается до GlcS, как показано на рис. 5.11. Были предложены различные формы ^-кривых (см. [13]), некоторые из которых приведены на рис. 5.12. Горизонтальная часть
этих кривых используется для объяснения явления хлопка. Однако скорее всего ^-кривые начинаются в нулевой точке. Рис. 5.9 показывает, что хлопок может произойти и в том случае, если /^-кривая начинается в нулевой точке. Форма R- кривой зависит от толщины пластины. Для толстых пластин, находящихся в плоском деформированном состоянии, они представляют собой пря-
мую горизонтальную линию. Для тонких пластин, находящихся в плоском напряженном состоянии, /^-кривая имеет ступеньку и возрастающий участок. Переходной зоне пластин промежуточной толщины соответствует ^-кривая, форма которой является чем-то средним между этими двумя крайними случаями. Теория ^-кривых до конца еще не разработана. В гл. VIII приведена дальнейшая информация о ^-кривых и процессе разрушения при плоском напряженном состоянии. Здесь же представлены R- кривые, полученные экспериментально. Податливость Уравнение (5.5) представляет собой соотношение между скоростью выделения энергии и податливостью. Таким образом, из соотношения между G и /С следует, что для плоского напряженного состояния
В случае плоской деформации в это соотношение следует добавить коэффициент (1 — Ъ?).1 Уравнение (5.22) позволяет определять К и G из податливости образца либо с помощью вычислений, либо экспериментально. Следует отметить, что податливость определяется по формуле
т. е. она определяется относительным перемещением точек приложения нагрузки. Уравнение (5.22) часто используют для вычислений К методом конечных элементов (см. § 13.3). Поучительным примером применения этого принципа является вычисление К и G для образца, имеющего форму двухконсольной балки (ДКБ) и изображенного на рис. 5.13. Если размер трещины измеряется от точки приложения нагрузки, то из теории простого изгиба следует, что относительное перемещение двух точек приложения нагрузки
Отсюда следует, что интенсивность выделения энергии
а коэффициент интенсивности напряжений
Уравнение (5.26) дает лишь грубое приближение величины коэффициента интенсивности напряжений. Расхождение возникает из-за того, что в балке образуются деформации сдвига (это можно учесть при выводе податливости), а также из-за того, что концы балок не жестко закреплены, а опираются на упругие шарниры.
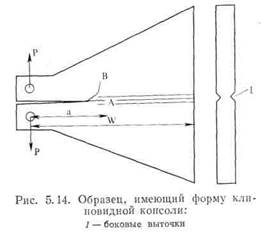
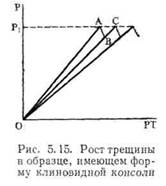
Из уравнения (5.26) следует, что коэффициент интенсивности напряжений для двухконсольной балки не зависел бы от размера трещины, если бы образец имел форму клина: если толщина увеличивается пропорционально а, так что отношение а/В постоянно, то величина К будет иметь одинаковые значения для трещин всех размеров. Это дало бы возможность исследовать процесс роста трещины при постоянных значениях К или G. Образец переменной толщины не очень практичен, поскольку процесс распространения трещины слишком сильно подвержен влиянию толщины образца. Поэтому Мостовой и др. [14] ввели в обращение образец в виде клиновидной двухконсольной балки, изображенной на рис. 5.14. Можно показать, что в этом образце при ограниченной области изменения размеров трещины величины К и G (вдоль тех же линий, что и в обычном ДКБ-образце) постоянны. Как показано на рис. 5.15, образец в виде клиновидной консоли может быть использован для изучения роста трещины при постоянном К- Образец нагружается вдоль линии ОА силой Ри при которой достигается интенсивность напряжений'(и интенсивность выделения энергии), необходимая для роста трещины. Трещина немного расширяется, что приводит к уменьшению нагрузки: Для того чтобы снова началось расширение трещины, необходимо повторное нагружение до той же силы Рь поскольку при этой нагрузке достигается то же значение К (обратите внимание на то, что, например, в образце с краевой трещиной при росте трещины то же значение К возникает
при меньших значениях Р, поскольку с ростом а значение К увеличивается по формуле К *=* СР~[/ка). При использовании образцов в виде двухконсольной балки часто оказывается, что путь трещины отклоняется от оси симметрии, как показано на рис. 5.14 (трещина В). Этого можно избежать, если проделать на боковых поверхностях образца выточки (см. рис. 5.14),
хотя наличие этих выточек усложняет вычисление податливости. Податливость можно также определить экспериментально следующим образом. Измеряя нагрузку и РТ, можно построить диаграмму «нагрузка — перемещение» (рис. 5.16, а). Эту работу следует повторить для различных размеров трещин. В соответствии с формулой С;= f= vIP, податливость определяется наклоном этих' линий. По измеренным значениям С строится график зависимости этой величины от размера трещины (рис. 5.16, б). Определяя наклон получающейся линии, можно найти производную от податливости дС/да, на основе которой с помощью уравнения (5.22) можно вычислить величины G и К (рис. 5.16, б). В -случае образца в виде клиновидной консольной балки можно
найти такую область изменения размеров трещины (между А и В), в которой G и К, фактически не зависят от длины трещины. Рис. 5.17 позволяет судить (см. [16, 17]) о точности измерений податливости путем сравнения их с результатами вычислений. Примечание. В образцах в виде двухконсольной балки податливость определяется раскрытием трещины. Это возможно только для образцов, нагружаемых по линии трещины. Для других типов образцов РТ нельзя использовать для определения податливости, поскольку относительное перемещение точек приложения нагрузки не равно РТ (см. [15]). J-интеграл
До сих пор лишь предполагалось, что зона пластичности при вершине трещины настолько мала, что применима теория упругости. Если это так, то пластические деформации при вершине трещины не оказывают влияния на интенсивность выделения энергии и величина G определяется упругим полем напряжений. Можно показать (см. [18]), что если зону пластичности при вершине трещины не считать пренебрежимо малой, то она будет оказывать влияние на интенсивность выделения энергии. Для того чтобы точно вычислить влияние пластических деформаций на величину G, нужно получить точное решение упругопластической задачи о поле напряжений при вершине трещины. Такое решение пока не получено, однако существует косвенный метод, в основе которого лежит /-интеграл, определяемый выражением (см. [19])
где 1 —замкнутый контур, который нужно обойти против часовой стрелки, окружающий в напряженном твердом теле некоторую область (рис. 5.18); Г—вектор напряжений, перпендикулярный контуру Г и направленный во внешнюю сторону,
что является энергией деформаций единицы объема. Можно показать (см. [1.9]), что если Г —замкнутый контур, то J?= 0. Райе [19] применил этот интеграл к задачам о трещине. Рассмот-
рим замкнутый контур ABCDEFA вокруг вершины трещины (рис. 5.19, а). Интеграл по этому контуру равен нулю. Поскольку на частях берегов трещины CD и AF значения Τ — 0 и dy = 0, их вклад в интеграл равен нулю. Поэтому интеграл по контуру ABC должен быть равен (с обратным знаком) интегралу по контуру DEF. Это означает, что независимо от того, берется ли /-интеграл по конту-
Для упругого случая /-интеграл можно вычислить, используя решение упругой задачи о поле напряжений. Отсюда следует (см. [19]), что
(5.29)
(5.30) Совершенно очевидно, что для упругого случая /-интеграл эквивалентен интенсивности выделения энергии. Райе также показал, что, вообще говоря,
где V — потенциальная энергия. В упругом случае уравнения (5.30) и (5.31) эквивалентны. Другими словами, / есть обобщенная функция выделения энергии за счет распространения трещины; эта функция может быть также справедлива и в том случае, когда вблизи вершины трещины имеются значительные пластические деформации. Поскольку /-интеграл не зависит от пути интегрирования, его можно определить менее сложным путем, выбирая путь интегрирования, вдоль которого интегрирование можно выполнить достаточно просто (т. е. вдоль краев· 120образца). Таким образом, интеграл дает возможность сравнительно просто определять интенсивность выделения энергии для случая, когда при вершине трещины имеется большая зона пластичности. Можно ожидать, что существует критическое значение J\c, при котором может начаться рост трещины. Так как это должно иметь силу и в упругом случае, то отсюда следует, что (5.32)
Уравнение (5.32) утверждает, что процесс роста трещины, связанный с большими пластическими деформациями, можно определить из J\c, зная значение Gic, которое было определено для случая, когда пластическими деформациями можно пренебречь, и наоборот.
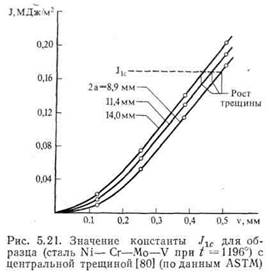
Согласно уравнению (5.31), J-интеграл можно найти из диаграммы «нагрузка — перемещение», точно так же как и в упругом случае, определяя податливость образца. Отличие заключается в том, что в результате пластичности на диаграмме «нагрузка — перемещение» может иметь место нелинейный участок. Этот факт схематически отображен на рис. 5.20, а. Площадь между двумя кривыми, связывающими нагрузку с перемещением для трещин, имеющих размеры а и а + da, равна (dV/da)da, т. е. эта площадь равна J. Кривые, связывающие нагрузки и перемещения в образце, можно получить экспериментально, последовательно увеличивая размер трещины, а площадь между двумя кривыми для трещин с мало отличающимися размерами — определить графически. Полученные таким образом значения J можно построить как функцию ν или а (рис. 5.20, б). Определяя значение υ при разрушении для трещин различных размеров, из рис. 5.20, б можно выяснить, происходит ли разрушение во всех случаях при одинаковом значении /. Подобные эксперименты были выполнены Биглеем и Лэндисом [20, 21]; некоторые из результатов экспериментов представлены на рис 5.21. Они обнаружили, что разрушение действительно проис- ходит при постоянном значении J\c, которое было равно G\c, определенной независимо. Аналогичные результаты были получены Коба-яши и др. [24]. При использовании /-интеграла требования, предъявляемые к размерам образца и его толщине, не такие строгие, как в случае тестов на определение G\c или Kic- В последнем случае пластические деформации при вершине трещины должны быть сравнительно малы,
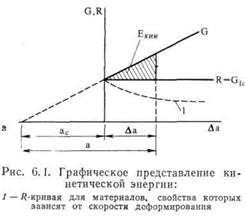
а поэтому размеры трещи представляется наиболее многообещающим в тех случаях, когда возникают большие пластические деформации (т. е. при плоской деформации). Однако в этих случаях передразрушением идет медленный рост трещины. В процессе медленного роста трещины за ее вершиной происходит разгрузка материала. До сих пор независимость /-интеграла от пути интегрирования была доказана только при использовании теории пластических деформаций (см. [19, 22, 23]), которая не предусматривает разгрузку материала. Поэтому в настоящее время критерий разрушения, основанный на использовании /-интеграла, следует применять лишь к процессу зарождения трещин. Кроме того, до сих пор не существует методики использования /-интеграла для описания процесса стабильного роста трещины. Примечание. Кобаяши и др. [24] с помощью инкрементальной теории пластического течения провели исследование задачи о росте трещины. Глава VI. ДИНАМИКА РОСТА ТРЕЩИНЫ И ЕГО ТОРМОЖЕНИЕ§ 6.1. Скорость распространения трещины и кинетическая энергия До сих пор рассматривалась задача о медленном росте трещины и о нестабильности этого процесса перед началом разрушения. В данной главе рассматривается вопрос о поведении трещины после возникновения нестабильности. Нестабильность, предшествующая разрушению, возникает тогда, когда при расширении трещины интенсивность выделения энергии упругих деформаций G постоянно превышает сопротивление росту трещины R. Избыток выделенной энергии (G — R) может перейти в кинетическую энергию. Эта кинетическая энергия связана с быстрым движением точек среды по обе стороны от траектории трещины при ее прохождении с большой скоростью. Разница между G и R определяет количество энергии, которое может перейти в кинетическую; следовательно, эта величина определяет скорость, с которой эта трещина будет распространяться в среде. Величины G и R представляют собой энергию, связанную с распространением трещины на Δα. Следовательно, общее количество энергии, которое может перейти в кинетическую энергию, после того как размер трещины увеличится на Δα, определяется интегралом от (G — R) на отрезке Δω. Этот интеграл представлен на рис. 6.1 заштрихованной областью. Изображенный на рис. 6.1 случай основан на трех упрощающих предположениях: 1) процесс распространения трещины происходит при постоянном напряжении; 2) интенсивность выделения энергии упругих деформаций не зависит от скорости распространения трещины; 3) сопротивление росту трещины постоянно. Что касается третьего предположения, то в предыдущей главе было показано, что во многих случаях величина R есть возрастающая функция, по крайней мере вовремя медленного распространения трещины. Этот факт не вносит существенных изменений в основные положения данной главы. Однако на величину R оказывает влияние
другое обстоятельство, которым нельзя пренебречь. Сопротивление росту трещины зависит от поведения материала при пластическом деформировании вблизи вершины трещины и его прочностных характеристик. Известно, что эти характеристики зависят от скорости деформирования. Поведение многих материалов зависит от скорости деформирования: при более высоких скоростях деформирования предел текучести увеличивается, а деформация, при которой происходит разрушение, уменьшается. При вершине распространяющейся с большой скоростью трещины скорости деформирования очень велики, поэтому следует ожидать, что при больших скоростях распространения трещины материал будет проявлять больше хрупких свойств. В результате материалы, свойства которых зависят от скорости деформирования, имеют убывающую 7?-кривую, показанную на рис. 6.1 штриховой линией. Второе предположение означает, что решение упругой задачи о статическом поле напряжений применимо и в динамическом случае. В действительности распределения напряжений в этих двух случаях из-за введения членов, зависящих от времени, различны. Этой задаче посвящен § 6.2. А в настоящем параграфе предполагается, что решение статической задачи приблизительно верно и для динамического случая. Первое предположение о неизменности напряжения несущественно. Ясно, что нестабильный рост трещины происходит при постоянной внешней нагрузке. Так как это является ограничивающим фактором, последующие рассуждения приводят к оценке верхней границы скорости распространения трещины. На практике во время роста трещины величина нагрузки может уменьшаться, что приводит к уменьшению G и, следовательно, к уменьшению значения (G — R) при условии, что величина R постоянна. Основываясь на теории размерностей, Мотт [1] получил выражение для кинетической энергии трещины. Элемент пластины с трещной, находящийся за вершиной этой трещины, перемещается на расстояния и и υ (см. гл. III), заданные соотношениями
Если вершина трещины передвигается, то выделенный элемент будет от нее удаляться: расстояние г от этого элемента до вершины трещины пропорционально размеру трещины. Следовательно, и перемещения пропорциональны размеру трещины:
Если с течением времени трещина растет, то эти перемещения также увеличиваются. Скорости этого движения соответственно равны:
в соотношении (6.3) точка означает производную по времени. Элемент среды массы т, движущийся со скоростью V, имеет кинетическую энергию mV2/2. Следовательно, кинетическая энергия материала пластины с трещиной, который движется со скоростями и и υ,
где ρ — удельная плотность. Следует заметить, что уравнение (6.4) справедливо для пластины единичной толщины. Подставляя в уравнение (6.4) соотношения (6.3), получим
В случае бесконечной пластины размер трещины α является единственным характерным размером, имеющим размерность длины. Площадь, вдоль которой выполняется интегрирование, должна быть пропорциональна а2. Это означает, что результат интегрирования должен быть пропорционален fea2, где k — константа:
Кинетическая энергия пропорциональна квадратам размера трещины и напряжения. Совершенно очевидно, что она должна быть пропорциональна удельной массе и квадрату скорости распространения трещины. Используя рис. 6.1, можно получить другое выражение для кинетической энергии:
Рассматривая случай, когда R — константа, а величина G при по-
Два выражения (6.6) и (6.9) для кинетической энергии можно приравнять друг к другу, получив
Выражение равно скорости звука v.. Значение
приблизительно u,do. Уравнение (6.10) описывает рост скорости распространения трещины от нуля при а =ас до верхней границы скорости 0,38us, когда a J а стремится к нулю; это имеет место тогда, когда трещина вырастает достаточно для того, чтобы выполнялось соотношение а» а с. На рис. 6.2 представлено графическое изображение соотношения (6.10). В работе Берри [3] выполнены подобные вычисления для образцов, имеющих форму двухконсольной балки. То же самое было сделано Хоаглэндом [41. Интегри- рование соотношения (6.7) можно провести и в том случае, если величина R является возрастающей функцией при условии, что эта зависимость R от размера трещины известна. Если для аппроксимации ^-кривой принята простая степенная функция (см. гл. VIII), то, как оказывается (см. [5]), результат вычислений все равно приводит к ограничению скорости распространения трещины величиной vs~\/2n/k. Измеренные скорости распространения трещин лежат значительно ниже их теоретических значений, вычисленных с помощью уравнения (6.10). В работе Блама [2] собраны результаты этих измерений. Некоторые из этих данных для трещин в хрупких материалах, полу- , пока не существует. Глава X. РАСПРОСТРАНЕНИЕ УСТАЛОСТНОЙ ТРЕЩИНЫ§ 10.1. Введение Определение кривой распространения усталостной трещины является существенной частью механики разрушения с точки зрения ее приложения при проектировании. Методики вычисления прочности при циклическом нагружении обладают рядом очевидных недостатков, однако параметры распространения усталостной трещины могут быть вычислены еще менее точно, несмотря на огромное количество исследований, посвященных этому предмету. Тем не менее успехи, достигнутые за последние годы, позволяют относиться к результатам этих вычислений с большим доверием. ■ В данной главе рассматриваются вопросы, связанные с распространением усталостной трещины, а также вопросы использования механики разрушения в циклических процессах, которое выражается соотношением между скоростью распространения усталостной трещины и коэффициентом интенсивности напряжений. Однако здесь лишь оцениваются достоинства и недостатки этого соотношения. Для детального рассмотрения физических аспектов данной проблемы читатель отсылается к соответствующей литературе [1—4]. Рассматриваются эффекты взаимодействия циклов различной амплитуды, а также эффект торможения роста трещины при перегрузках в процессе циклического нагружения (см. [5]); однако данные вопросы рассматриваются только с точки зрения их применения в инженер-, ной практике. § 10.2. Рост трещины и коэффициент интенсивности напряжений В упругом случае для описания поля напряжений при вершине трещины достаточно знать коэффициент интенсивности напряжений. В случае, когда размер зоны пластичности мал по сравнению с длиной трещины, коэффициент интенсивности напряжений еще дает возможность удовлетворительно описать распределение напряжений вокруг вершины трещины. Если две различные трещины обладают одинаковым распределением напряжений, т. е. имеют один и тот же коэффициент интенсивности напряжений, то они ведут себя одинаково и распространяются с одинаковыми скоростями. Расстояние, на которое усталостная трещина распространяется за один цикл, определяется диапазоном изменения коэффициента интенсивности напряжений Δ/0
|
||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 621; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.129.73.198 (0.017 с.) |

 будет достигнут критический размер трещины ас, при котором возникает неустойчивость, предшествующая разрушению. Этот процесс проиллюстрирован на рис. 5.7.
будет достигнут критический размер трещины ас, при котором возникает неустойчивость, предшествующая разрушению. Этот процесс проиллюстрирован на рис. 5.7.
 чина слишком мала для того, чтобы трещина росла. Напряжение может быть далее увеличено до σ.; скорость выделения энергии при этом будет задана точкой В
чина слишком мала для того, чтобы трещина росла. Напряжение может быть далее увеличено до σ.; скорость выделения энергии при этом будет задана точкой В

 (5.20)
(5.20) (5.21)
(5.21)


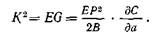 (5.22)
(5.22)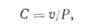 (5.23)
(5.23) (5.24) Следовательно, податливость образца
(5.24) Следовательно, податливость образца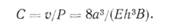
 (5.25)
(5.25) (5.26)
(5.26)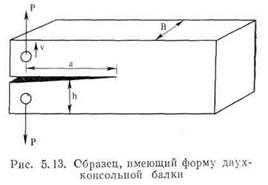



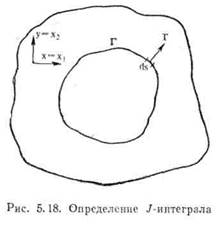
 и — перемещение в направлении оси х; ds — элемент контура Г. Кроме того, Г"7
и — перемещение в направлении оси х; ds — элемент контура Г. Кроме того, Г"7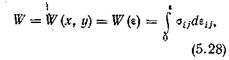

 ру ABC или FED, результат будет один и тот же: интеграл не зависит от пути интегрирования, т.е. /ri = /re (рис. 5.19,6). Обратите внимание на то, что этот интеграл, не зависящий от пути интегрирования, берется не по замкнутому контуру: пределы интегрирования лежат на краях трещины.
ру ABC или FED, результат будет один и тот же: интеграл не зависит от пути интегрирования, т.е. /ri = /re (рис. 5.19,6). Обратите внимание на то, что этот интеграл, не зависящий от пути интегрирования, берется не по замкнутому контуру: пределы интегрирования лежат на краях трещины.
 Райсом было показано [19], что вычисление интеграла (5.29) приводит к соотношению
Райсом было показано [19], что вычисление интеграла (5.29) приводит к соотношению
 (5.31)
(5.31)

 (6.1)
(6.1) (6.2)
(6.2) (6.3)
(6.3) (6.4)
(6.4) (6.5)
(6.5) (6.6)
(6.6) (6.7)
(6.7) стоянном напряжении определяется решением статической задачи, получаем выражение для кинетической энергии
стоянном напряжении определяется решением статической задачи, получаем выражение для кинетической энергии
 Константа R в начале нестабильного процесса равна G\c (величина которого задана соотношением G\c =no2ajE). Подставляя в соотношение (6.8) равенство R = G\c и проводя интегрирование, получаем (для двух вершин трещины)
Константа R в начале нестабильного процесса равна G\c (величина которого задана соотношением G\c =no2ajE). Подставляя в соотношение (6.8) равенство R = G\c и проводя интегрирование, получаем (для двух вершин трещины)

 есть скорость продольных волн в среде, т. е. оно
есть скорость продольных волн в среде, т. е. оно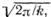 как оказывается, равно
как оказывается, равно




