
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Квантовый гармонический осцилляторСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
В классической физике широко распространено понятие гармонический осциллятор. Гармонический осциллятор используется для описания поведения множества систем, где возможны гармонические колебания. Характерная особенность гармонического осциллятора – движение материальной точки под воздействием квазиупругой силы F = -kx. Потенциальная энергия частицы в такой системе
Поскольку зависимость потенциальной энергии осциллятора от координаты квадратичная, можно сказать, что гармонический осциллятор – это частица в параболической потенциальной яме. Если волновые свойства колеблющейся частицы заметны, то гармонический осциллятор является квантовым. Особенности поведения квантового гармонического осциллятора, т.е. квантовой частицы в параболической потенциальной яме, можно узнать, решив уравнение Шрёдингера для этой системы:
Общий вид решения довольно сложен. Поэтому решение рассматриваться не будет. Рассмотрим лишь выводы, сделанные на основе анализа решения. Квантовому гармоническому осциллятору разрешены лишь значения энергии, отвечающие уравнению
где n = 0, 1, 2... Таким образом, энергия квантового гармонического осциллятора квантуется. Минимальная возможная энергия квантового гармонического осциллятора не равна нулю (Е min = h n0/2), т.е. квантовый гармонический осциллятор не может покоится. Он всегда должен двигаться.
Следует отметить важную особенность волновой функции, описывающей квантовый гармонический осциллятор. Эта особенность заключается в том, что волновая функция за пределами ямы отлична от нуля. Другими словами, квантовый гармонический осциллятор может оказаться за стенками потенциальной ямы, чего классический осциллятор не может. На рисунке в качестве примера показан график квадрата модуля волновой функции квантовой частицы от координаты (точки ± х о – координаты краев ямы; классический осциллятор за этими точками не может оказаться никогда). Следует отметить, что примеры, рассмотренные в трех последних разделах, абстрактны. В реальном мире такие ситуации не встречаются. Но анализ этих частных примеров позволил выявить некоторые особенности, присущие реальным квантовым системам. Поэтому анализ этих примеров следует расценивать как первый шаг в направлении к анализу реальных ситуаций (они будут рассмотрены в следующей части). ЛИТЕРАТУРА 1. Арсентьев В.В., Кирпиченков В.Я. и др. Курс физики. – СПб.: Лань, 2. Баранов А.В., Невская Г.Е. и др. Колебания и волны. Оптика. Квантовая механика. – Новосибирск, 1994. 3. Горелик Г.С. Колебания и волны. – М.: ГИТТЛ, 1950. 4. Джанколи. Физика. – М.: Мир, 1989. – Т. 1, 2. 5. Ландсберг Г.С. Оптика. – М.: Наука, 1976. 6. Орир. Физика. – М.: Мир, 1981. – Т. 1, 2. 7. Путилов К.А. Курс физики. – М.: ОГИЗ, 1945. 8. Савельев И.В. Курс общей физики. – М.: Наука, 1978. – Т. 2. 9. Сивухин Д.В. Общий курс физики. – М.: Наука, 1977. – Т. 3. 10. Спасский Б.И. История физики. – М.: Высш. шк., 1977. – Т.1, 2. 11. Трофимова Т.И. Курс физики. – М.: Высш. шк., 1990. 12. Физика. Большой энциклопедический словарь. – М.: Большая Российская Энциклопедия, 1999.
ОГЛАВЛЕНИЕ 1 Волновая оптика ………………………………………...3 1.1. Интерференция волн............................................................... 3 1.1.1. Интерференция волн от двух синфазных источников ……………………………………………………………4 1.1.2. Когерентность ……………………………….9 1.1.3. Интерференция света в тонких пленках …11 1.1.4. Диаграмма направленности …………………….15 1.1.5. Многолучевая интерференция …………...16 1.2. Дифракция………………………………………………. 24 1.2.1. Принцип Гюйгенса–Френеля …………………….25 1.2.2. Дифракция Френеля. Метод зон Френеля…… …26 1.2.3. Дифракция Фраунгофера на щели …………...30 1.2.4. Дифракция на двух щелях …………………….35 1.2.5. Дифракционная решетка …………………….39 1.3. Естественный и поляризованный свет. Виды поляризации…………………………………………………………………... ….42 1.3.1. Способы получения поляризованного света …43 1.3.2. Явление двойного лучепреломления …………..47 2. Квантовая механика ……………………………………….51 2.1. Кризис классической физики............................................. 51 2.2. Тепловое излучение.............................................................. 51 2.2.1. Характеристики теплового излучения …………..52 2.2.2. Равновесный характер теплового излучения …53 2.2.3. Абсолютно черное тело …………………….53 2.2.4. Закон Кирхгофа ………………………………54 2.2.5. Закон Стефана–Больцмана ……………………..55 2.2.6. Закон смещения Вина ……………………..56 2.2.7. Формулы Рэлея–Джинса и Планка …………...57 2.3. Явление внешнего фотоэффекта....................................... 58 2.4. Зависимость фототока от разности потенциалов между катодом и анодом..................................................... 61 2.5. Фотоны..................................................................................... 63 2.6. Корпускулярно-волновой дуализм. Гипотеза де Бройля 65 2.7. Волновая функция и ее физический смысл.................... 67 2.8. Свойства волн де Бройля.................................................... 68 2.9. Соотношение неопределенностей.................................... 70 2.10. Уравнение Шрёдингера.................................................... 72 2.11. Уравнение Шрёдингера для стационарных состояний 74 2.12. Движение свободной частицы........................................ 75 2.13. Отражение частицы от потенциальной ступеньки... 76 2.14. Туннельный эффект............................................................ 80 2.15. Частица в бесконечно глубокой потенциальной яме 81 2.16. Частица в бесконечно глубокой двумерной потенциальной яме. Вырождение энергетических уровней........................... 86 2.17. Квантовый гармонический осциллятор....................... 87 Литература........................................................................................................... 89
|
||||||||||
|
Последнее изменение этой страницы: 2016-12-12; просмотров: 811; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.2 (0.01 с.) |

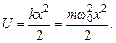



 Более тщательный анализ может выявить еще одно интересное свойство квантового гармонического осциллятора – оказывается, квантовый гармонический осциллятор не может менять свою энергию произвольно. Ему разрешен лишь переход на один из соседних уровней энергии, т.е. n может измениться только на единицу: D n = ±1. Другими словами, энергия квантового гармонического осциллятора может изменяться только порциями, равными h n0.
Более тщательный анализ может выявить еще одно интересное свойство квантового гармонического осциллятора – оказывается, квантовый гармонический осциллятор не может менять свою энергию произвольно. Ему разрешен лишь переход на один из соседних уровней энергии, т.е. n может измениться только на единицу: D n = ±1. Другими словами, энергия квантового гармонического осциллятора может изменяться только порциями, равными h n0.


