
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Дифракция Френеля. Метод зон ФренеляСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
Дифракцией Френеля называют дифракцию сферических световых волн. Рассмотрим это явление более подробно. Итак, пусть в точке S расположен точечный источник света. Рассчитаем амплитуду и интенсивность волны, дошедшей от источника в точку Р. Если источник света точечный, то испускаемая им волна является сферической. Любая волновая поверхность такой волны – сфера с центром в точке S. Разобьем волновую поверхность на кольцевые зоны так, чтобы расстояние от точки Р до краев соседних зон отличалось на l/2.
Для этого увеличим длину b отрезка OP на l/2 и проведем новым отрезком окружность на волновой поверхности. В результате получим первую зону Френеля. Затем увеличим длину этого отрезка еще на l/2 и вновь проведем окружность на волновой поверхности. Получим вторую зону Френеля. Продолжая построение, получим совокупность зон Френеля. В соответствии с принципом Гюйгенса–Френеля каждая точка волновой поверхности представляет собой источник волн, причем эти источники синфазны. Расстояние от точек, расположенных на внешнем крае соседних зон, до точки Р отличаются на l/2, поэтому они возбудят в точке Р противофазные колебания. Точно так же будут соотноситься по фазе колебания, возбужденные источниками, одинаково удаленными от внешнего края соседних зон. Поэтому можно сказать, что соседние зоны возбуждают в точке наблюдения противофазные колебания. Последнее утверждение означает, что амплитуда результирующего колебания в точке Р может быть найдена как
где Аi – амплитуда колебаний, возбуждаемых i -й зоной в точке наблюдения. Френелем было доказано, что амплитуда колебаний, возбуждаемых i -й зоной в точке наблюдения, монотонно уменьшается по мере увеличения номера зоны. Следовательно, А 1 > А 2 > А 3 >... > Аn. Поскольку амплитуда убывает монотонно, можно считать, что С учетом этого результирующая амплитуда колебаний, возбужденных на экране полностью открытой волновой поверхностью, равна
Таким образом, полностью открытая волновая поверхность возбуждает в точке наблюдения колебания, амплитуда которых равна половине амплитуды колебаний, возбужденных первой зоной Френеля. Если на пути волны поставить непрозрачный экран с круглым отверстием, радиус которого равен радиусу первой зоны Френеля, то амплитуда результирующего колебания равна амплитуде колебаний, возбуждаемых в точке наблюдения только первой зоной Френеля (все остальные зоны закрыты и не возбуждают колебаний в точке наблюдения): А = А 1. Это означает, что амплитуда колебаний в точке Р возросла в два раза по сравнению с предыдущей ситуацией. Интенсивность же возросла в четыре раза*! Этот вывод не означает, что, поставив препятствие на пути света, мы сильнее осветили весь экран. Лучи, прошедшие через отверстие, будут интерферировать. Это приведет к перераспределению энергии волны, прошедшей на экран. В результате против центра отверстия будет максимум интерференции и точка Р окажется освещенной гораздо ярче соседних. По мере удаления от точки Р яркость света будет уменьшаться, так что точка Р будет окружена темным кольцом. За темным кольцом будет расположено более яркое и т.д. Если увеличить радиус отверстия до радиуса второй зоны Френеля, то А = А 1 – А 2. Можно показать, что амплитуды колебаний, возбужденных соседними зонами Френеля, очень мало отличаются по величине, поэтому А 1 – А 2 » 0. Следовательно, при таком отверстии точка Р практически не освещена. Обратите внимание: вывод касается только точки Р. Вокруг точки, как и в предыдущем примере, будут расположены дифракционные максимумы и минимумы кольцевой формы. Если в отверстии укладывается целое число зон Френеля, то амплитуда колебаний в точке Р рассчитывается по формуле
где Ai – амплитуда колебаний, возбужденных на экране последней открытой зоной Френеля; знак «плюс» используется, если открыто нечетное число зон, «минус» – если четное. Из сказанного выше следует простой вывод: точка Р будет ярко освещена, если в отверстии укладывается нечетное число зон Френеля, и, наоборот, точка Р практически не будет освещена, если в отверстии уложится четное число зон Френеля. Для того чтобы определить, сколько зон уложится в круглом отверстии, необходимо уметь рассчитывать радиус зон Френеля. Найдем выражение для его расчета.
На рисунке изображена i -я зона Френеля. Символами обозначены следующие величины: S – источник света, а – радиус волновой поверхности, b – расстояние от точки Р до волновой поверхности, ri – радиус i -й зоны Френеля, hi – длина отрезка, соединяющего точку О и точку пересечения перпендикуляра, опущенного от края зоны Френеля на отрезок SP. Из рисунка видно, что
Полученное выражение позволяет найти радиус любой зоны Френеля и оценить результат дифракции на различных препятствиях круглой формы (экран с круглым отверстием, непрозрачный диск). Например, если а = b = 1 м, l = 0,5 мкм, то радиус первой зоны Френеля И еще одна деталь. Поскольку полностью открытая волновая поверхность оказывает действие, эквивалентное действию половины первой зоны Френеля, то можно сказать, что свет, идущий от точечного источника S, воспринимается нами как тонкий прямой луч (в рассмотренном выше примере радиус луча 0,5×10-3 м). Этим и объясняется эффект, который принято называть прямолинейностью распространения света. Хотя в соответствии с принципом Гюйгенса–Френеля свет от точечного источника идет во все стороны, мы воспринимаем его как узкий прямолинейный луч.
|
||||
|
Последнее изменение этой страницы: 2016-12-12; просмотров: 466; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.59.91.59 (0.009 с.) |


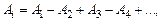
 , т.е. амплитуда колебаний, возбужденных на экране какой-либо зоной Френеля, равна полусумме амплитуд, возбужденных там же соседними зонами.
, т.е. амплитуда колебаний, возбужденных на экране какой-либо зоной Френеля, равна полусумме амплитуд, возбужденных там же соседними зонами.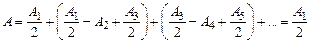 *.
*. ,
,
 ;
; ;
; ;
; ;*
;* ;
; .
. . Следовательно, если в непрозрачном экране сделать отверстие радиусом 0,5.10-3м, то точка Р будет ярко освещена (максимум дифракции). Если же радиус отверстия увеличить в
. Следовательно, если в непрозрачном экране сделать отверстие радиусом 0,5.10-3м, то точка Р будет ярко освещена (максимум дифракции). Если же радиус отверстия увеличить в  раз, то точка Р будет практически не освещена.
раз, то точка Р будет практически не освещена.


