
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Дифракция Френеля от простейших преград.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Дифракция от круглого отверстия. Рассмотрим дифракцию в сходящихся лучах, или дифракцию Френеля, осуществляемую в том случае, когда дифракционная картина наблюдается на конечном расстоянии от препятствия, вызвавшего дифракцию. Поставим на пути сферической световой волны непрозрачный экран с круглым отверстием радиуса
Рис. 17.13 На продолжении этого перпендикуляра возьмем точку M и рассмотрим, что мы будем наблюдать на экране. Разобьем открытую часть волновой поверхности на зоны Френеля. Вид дифракционной картины зависит от числа зон Френеля, открываемых отверстием. Амплитуда результирующего колебания, возбуждаемого в точке М всеми зонами
Таким образом, когда отверстие открывает нечетное число зон Френеля, то амплитуда (интенсивность) в точке М будет больше, чем при свободном распространении волны; если четное, то амплитуда (интенсивность) будет равна нулю, как показано на рис. 17.13. Естественно, что если Дифракция от диска. Сферическая волна, распространяющаяся от точечного источника S, встречает на своем пути диск (рис. 17.14).
Рис. 17.14 Точка M лежит на перпендикуляре к центру диска. Первая зона Френеля строится от края диска и т. д. Амплитуда световых колебаний в точке M равна половине амплитуды, обусловленной первой открытой зоной. Если размер диска невелик (охватывает небольшое число зон), то действие первой зоны немногим отличается от действия центральной зоны волнового фронта. Таким образом, освещенность в точке M будет такой же, как и в отсутствие экрана. Вследствие симметрии центральная светлая точка будет окружена кольцами света и тени (вне границ геометрической тени). Парадоксальное, на первый взгляд, заключение, в силу которого в самом центре геометрической тени может находиться светлая точка, было выдвинуто Пуассоном в 1818 г. и впоследствии было названо его именем. «Пятно Пуассона» подтверждает правильность теории Френеля. 17.7. Дифракция в параллельных лучах (дифракция Фраунгофера) Тип дифракции, при котором дифракционная картина образуется параллельными пучками, называется дифракцией Фраунгофера. Параллельные лучи проявятся, если источник и экран находятся в бесконечности. Практически используется две линзы: в фокусе одной – источник света, а в фокусе другой – экран. Хотя принципиально дифракция Фраунгофера не отличается от дифракции Френеля, но практически именно этот случай важен, так как именно этот тип дифракции используется во многих дифракционных приборах (дифракционная решетка, например). Кроме того, здесь математический расчет проще и позволяет решать количественную задачу до конца (дифракцию Френеля мы рассматривали качественно). Дифракция света на одной щели. Пусть в непрерывном экране есть щель: ширина щели Если на ширине щели укладывается четное число таких зон, то в точке
Картина будет симметричной относительно главного фокуса точки Интенсивность света Рассмотрим влияние ширины щели. Т.к. условие минимума имеет вид Из этой формулы видно, что с увеличением ширины щели b положения минимумов сдвигаются к центру, центральный максимум становится резче. При уменьшении ширины щели b вся картина расширяется, расплывается, центральная полоска тоже расширяется, захватывая все большую часть экрана, а интенсивность ее уменьшается.
Рис. 17.15 Дифракция света на дифракционной решетке. Одномерная дифракционная решетка представляет собой систему из большого числа N одинаковых по ширине и параллельных друг другу щелей в экране, разделенных также одинаковыми по ширине непрозрачными промежутками (рис. 17.16). Дифракционная картина на решетке определяется как результат взаимной интерференции волн, идущих от всех щелей, т.е. в дифракционной решетке осуществляется многолучевая интерференция когерентных дифрагированных пучков света, идущих от всех щелей. Обозначим: b – ширина щели решетки; а – расстояние между щелями; Линза собирает все лучи, падающие на нее под одним углом и не вносит никакой дополнительной разности хода.
Пусть луч 1 падает на линзу под углом φ (угол дифракции). Световая волна, идущая под этим углом от щели, создает в точке
Условие максимума для дифракционной решетки будет иметь вид:
где m = ± 1, ± 2, ± 3, …. Максимумы, соответствующие этому условию, называются главными максимумами. Значение величины m, соответствующее тому или иному максимуму называется порядком дифракционного максимума. В точке F 0 всегда будет наблюдаться нулевой или центральный дифракционный максимум. Так как свет, падающий на экран, проходит только через щели в дифракционной решетке, то условие минимума для щели и будет условием главного дифракционного минимума для решетки:
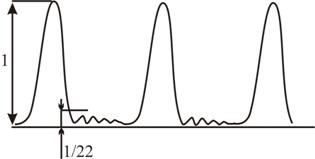
Конечно, при большом числе щелей, в точки экрана, соответствующие главным дифракционным минимумам, от некоторых щелей свет будет попадать и там будут образовываться побочные дифракционные максимумы и минимумы (рис. 17.17). Но их интенсивность, по сравнению с главными максимумами, мала (≈ 1/22). При условии волны, посылаемые каждой щелью, будут гаситься в результате интерференции и появятся дополнительные минимумы. Количество щелей определяет световой поток через решетку. Чем их больше, тем большая энергия переносится волной через нее. Кроме того, чем больше число щелей, тем больше дополнительных минимумов помещается между соседними максимумами. Следовательно, максимумы будут более узкими и более интенсивными. Дифракционная решетка разлагает белый свет на составляющие, причем отклоняет свет с большей длиной волны (красный) на больший угол (в отличие от призмы, где все происходит наоборот). Это свойство дифракционных решеток используется для определения спектрального состава света (дифракционные спектрографы, спектроскопы, спектрометры). 17.8. Дифракция на пространственных решетках.Формула Вульфа-Бреггов. Пространственной, или трехмерной, дифракционной решеткой называется такая оптически неоднородная среда, в которой неоднородности периодически повторяются при изменении всех трех пространственных координат. Условия прохождения света через обычную дифракционную решетку периодически изменяются только в одном направлении, перпендикулярном к оси щели. Поэтому такую решетку называют одномерной. Простейшую двумерную решетку можно получить, сложив две одномерные решетки так, чтобы их щели были взаимно перпендикулярны. Главные максимумы двумерной решетки должны одновременно удовлетворять условию максимума для каждой из решеток:
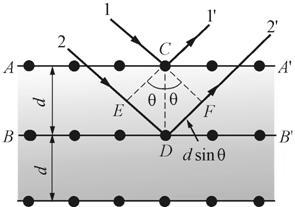
где φ - угол между направлением на главный максимум (направление луча) и нормалью к решетке; m – порядок дифракционного максимума. Дифракционная картина представляет собой систему светлых пятен, расположенных в определенном порядке на плоскости экрана. Размеры этих пятен уменьшаются при увеличении числа щелей, а яркость возрастает. Такая же картина получается, если на одно стекло нанести ряд взаимно перпендикулярных полос. Дифракция наблюдается также и на трехмерных структурах. Всякий монокристалл состоит из упорядоченно расположенных атомов (ионов), образующих пространственную трехмерную решетку (естественная пространственная решетка). Период атомной решетки порядка В 1913 г. русский физик Г.В. Вульф и английские ученые отец и сын Генри и Лоуренс Брэгги, независимо друг от друга, предложили простой метод расчета дифракции рентгеновских лучей в кристаллах. Они полагали, что дифракцию рентгеновских лучей можно рассматривать как результат отражения рентгеновских лучей от плоскостей кристалла. Это отражение, в отличие от обычного, происходит лишь при таких условиях падения лучей на кристалл, которые соответствуют максимуму интерференции для лучей, отраженных от разных плоскостей. Направим пучок рентгеновских лучей 1 и 2 на две соседние плоскости кристалла Абсолютный показатель преломления всех веществ для рентгеновских лучей равен 1. Поэтому оптическая разность хода между лучами
где θ – угол между падающими и отраженными лучами и плоскостью кристалла (угол скольжения). Интерференционные максимумы должны удовлетворять условию Вульфа–Брэггов:
Рис. 17.18 Из формулы (17-18) видно, что дифракция будет наблюдаться лишь при Из (17-18) следует, что наблюдение дифракционных максимумов возможно только при определенных соотношениях между λ и θ. Этот результат лежит в основе спектрального анализа рентгеновского излучения, так как длину волны определяют по известным d, m и измеренному на опыте углу. Исследуя дифракцию рентгеновских лучей, можно решить и обратную задачу: если известна длина волны λ рентгеновских лучей, можно определить период кристаллической решетки d и ориентацию атомных плоскостей в пространстве. Эта идея была высказана немецким физиком М. Лауэ в 1912 г. и явилась существенным вкладом в развитие физики твердого тела.
|
|||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-16; просмотров: 1567; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.62 (0.011 с.) |

 . Экран расположен так, что перпендикуляр, опущенный из S на непрозрачный экран, попадает точно в центр отверстия (рис. 17.13).
. Экран расположен так, что перпендикуляр, опущенный из S на непрозрачный экран, попадает точно в центр отверстия (рис. 17.13).
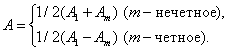
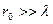 , то никакой дифракционной картины не будет.
, то никакой дифракционной картины не будет.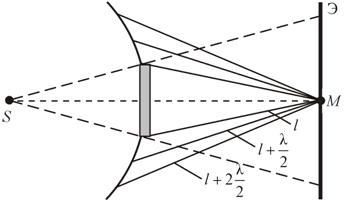

 , длина щели (перпендикулярно плоскости листа)
, длина щели (перпендикулярно плоскости листа) 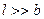 (рис. 17.15). На щель падают параллельные лучи света. Для облегчения расчета считаем, что в плоскости щели АВ амплитуды и фазы падающих волн одинаковы. Разобьем щель на зоны Френеля так, чтобы оптическая разность хода между лучами, идущими от соседних зон, была равна
(рис. 17.15). На щель падают параллельные лучи света. Для облегчения расчета считаем, что в плоскости щели АВ амплитуды и фазы падающих волн одинаковы. Разобьем щель на зоны Френеля так, чтобы оптическая разность хода между лучами, идущими от соседних зон, была равна  .
. (побочный фокус линзы) будет наблюдаться минимум интенсивности, а если нечетное число зон, то максимум интенсивности:
(побочный фокус линзы) будет наблюдаться минимум интенсивности, а если нечетное число зон, то максимум интенсивности: – условие минимума интенсивности;
– условие минимума интенсивности;
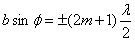 – условие максимума интенсивности
– условие максимума интенсивности
 . Знак плюс и минус соответствует углам, отсчитанным в ту или иную сторону.
. Знак плюс и минус соответствует углам, отсчитанным в ту или иную сторону.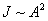 . Как видно из рис.17.15, центральный максимум по интенсивности превосходит все остальные.
. Как видно из рис.17.15, центральный максимум по интенсивности превосходит все остальные. , отсюда
, отсюда 
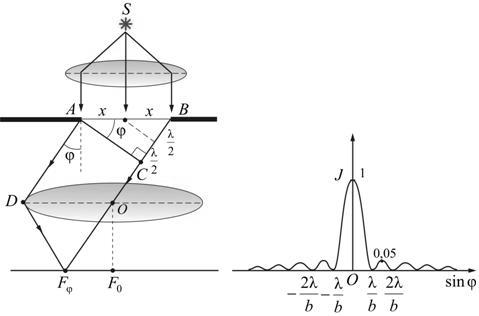
 – постоянная дифракционной решетки.
– постоянная дифракционной решетки.
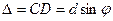
 ,
,
 ,
, и
и 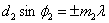 ,
, ; длина волны света
; длина волны света  . При таких условиях никаких дифракционных явлений на атомных дифракционных решетках с видимым светом не будет. Нужно излучение с меньшей длиной волны, например рентгеновское. Для рентгеновских лучей кристаллы твердых тел являются идеальными дифракционными решетками.
. При таких условиях никаких дифракционных явлений на атомных дифракционных решетках с видимым светом не будет. Нужно излучение с меньшей длиной волны, например рентгеновское. Для рентгеновских лучей кристаллы твердых тел являются идеальными дифракционными решетками.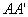 и
и  (рис. 17.18).
(рис. 17.18). и
и 
 ,
, , (m = 1, 2, 3,....).
, (m = 1, 2, 3,....).
 . Т. е. при условии
. Т. е. при условии 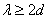 будут отсутствовать дифракционные максимумы. Поэтому условие
будут отсутствовать дифракционные максимумы. Поэтому условие 


