Поток вектора напряженности. Теорема Остроградского-Гаусса
Похожие статьи вашей тематики
Пусть имеем однородное электрическое поле (напряженность которого одинакова во всех точках пространства) с напряженностью  , которое пронизывает некоторую плоскую поверхность площади S, тогда скалярное , которое пронизывает некоторую плоскую поверхность площади S, тогда скалярное

произведение  будет называться потоком вектора напряженности будет называться потоком вектора напряженности  через поверхность S, (рис. 11.5), т.е. через поверхность S, (рис. 11.5), т.е.
 , (11-14) , (11-14)
где  — есть вектор, равный произведению величины площади на нормаль к этой поверхности, Еn -проекция вектора — есть вектор, равный произведению величины площади на нормаль к этой поверхности, Еn -проекция вектора  на нормаль, на нормаль,  к площадке. к площадке.
В общем случае поле может быть неоднородным, поверхность неплоской. В этом случае поверхность можно мысленно разбить на бесконечно малые элементарные площадки dS, которые можно считать плоскими, а поле вблизи них однородным. В таком случае поток через элементарную площадку
 . (11-15) . (11-15)
Полный поток вектора напряженности через поверхность S
 . (11-16) . (11-16)
Найдем поток вектора напряженности электрического поля, создаваемого
точечным зарядом q, через сферическую поверхность радиуса r.
Площадь ее поверхности 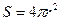 . Силовые линии электрического поля, идут по радиусам к поверхности сферы и поэтому угол между векторами . Силовые линии электрического поля, идут по радиусам к поверхности сферы и поэтому угол между векторами  и и  равен нулю. равен нулю.
 . (11-17) . (11-17)
Можно показать, что поток через замкнутую поверхность не зависит от формы поверхности и от расположения зарядов в ней.
Рассмотрим поток, создаваемый системой зарядов, сквозь замкнутую поверхность произвольной формы, внутри которой они находятся (рис.11.6):  . .

Согласно принципу суперпозиции  поэтому поэтому
 таким образом таким образом  . (11-18) . (11-18)
Итак, мы доказали теорему Остроградского-Гаусса:
«Полный поток вектора напряженности электростатического поля через произвольную замкнутую поверхность равен алгебраической сумме зарядов, охватываемых этой поверхностью, деленной на 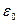 » »
Теорема позволяет рассчитать электрические поля, создаваемые заряженными телами различной формы:
1) Поле равномерно заряженной, бесконечно протяженной плоскости (рис. 11.7).
Построим цилиндр, ось которого перпендикулярна к поверхности, и применим теорему Остроградского-Гаусса.

 , ,
т.к.  , то , то
 , ,
отсюда  , (11-19) , (11-19)
где s = q/S —поверхностная плотность заряда, измеряемая в СИ в Кл/м2.
2) Поле между двумя бесконечно протяженными, разноименно заряженными параллельными плоскостями (рис. 11.8). Вне внутреннего промежутка,  = 0 т. к. поля, созданные разноименно заряженными параллельными пластинами, направлены противоположно друг другу; = 0 т. к. поля, созданные разноименно заряженными параллельными пластинами, направлены противоположно друг другу;
между плоскостями  . .
Итак: 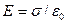 . (11-20) . (11-20)

По этой же формуле определяется напряженность электрического поля вблизи заряженного проводника.
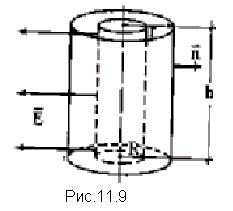
Поле заряженного цилиндра: заряженный цилиндр радиуса R, (рис.11.9), окружим коаксиальной цилиндрической поверхностью радиуса r; поток вектора  через основания равен нулю, т. к. через основания равен нулю, т. к. 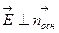 , где , где 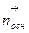 - внешняя нормаль к основаниям цилиндра; поток через боковую поверхность - внешняя нормаль к основаниям цилиндра; поток через боковую поверхность  , ,
3) здесь h — высота цилиндра.
Согласно теореме Гаусса – Остроградского при 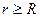 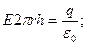
 (11-21) (11-21)
где t = q/ h — линейная плотность заряда, которая измеряется в Кл/м.
Когда r < R, то  = 0. = 0.
4) Поле заряженной сферы: поток вектора  через поверхность сферы радиуса r, (рис. 11.10), которая окружает заряженную сферу, имеющую радиус R,при r через поверхность сферы радиуса r, (рис. 11.10), которая окружает заряженную сферу, имеющую радиус R,при r  R R 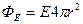 . По теореме Остроградского-Гаусса . По теореме Остроградского-Гаусса
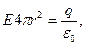 oткуда oткуда  (11-22) (11-22)


т.е. вне заряженной сферы поле такое же, как и поле точечного заряда той же величины, помещенного в центре сферы. Внутри сферы нет зарядов и поэтому поле там отсутствует, т. е. при г < R имеем,  = 0. Это свойство используют для экранировки от полей внешних зарядов. = 0. Это свойство используют для экранировки от полей внешних зарядов.
|