Энергетические соотношения в колебательных процессах.
Для груза, совершающего гармонические колебания, значение кинетической энергии mv2/2 находится прямой подстановкой в величину кинетической энергии выражения для скорости колебательного движения, определяемой выражением (5-17):
Екин =   . (5-25) . (5-25)
Максимальное значение этой энергии, очевидно, равно
 (5-26) и достигается в момент, когда тело проходит положение равновесия. Пройдя это положение тело продолжает двигаться по инерции и вызывает деформацию пружины. При этом кинетическая энергия движущегося тела переходит в потенциальную энергию деформированной пружины Епот : (5-26) и достигается в момент, когда тело проходит положение равновесия. Пройдя это положение тело продолжает двигаться по инерции и вызывает деформацию пружины. При этом кинетическая энергия движущегося тела переходит в потенциальную энергию деформированной пружины Епот :
Епот =  . (5-27) . (5-27)
Максимальное значение этого вида механической энергии равно:
 . (5-28) . (5-28)
При незатухающих колебаниях  , поэтому имеет место сохранение механической энергии: , поэтому имеет место сохранение механической энергии:  . В этом случае суммарная энергия сохраняет свою величину в любой момент времени (выражения (5-25) и (5-27)): . В этом случае суммарная энергия сохраняет свою величину в любой момент времени (выражения (5-25) и (5-27)):
 , (5-29) , (5-29)
где учтено, что sin2 a + cos2 a = 1 и  . .
Если колебания являются затухающими, за каждый период колебаний суммарная энергия колеблющегося тела уменьшается на величину работы против сил трения. В этом случае колеблющееся тело или любая система, в которой происходят колебания, характеризуется так называемым качеством или добротностью системы Q, которая определяется как способность системы к превращениям одного вида механической энергии в другой (т.е. кинетической в потенциальную или наоборот). Количественно добротность определяется (с точностью до коэффициента 2p) как отношение максимальной энергии упругой деформации (или максимальной кинетической энергии колеблющейся системы) к средней величине потерь энергии в системе за период. Известно, что среднее значение любой переменной величины <у> за период определяется соотношением:
< у > =  . .
Мгновенное значение силы вязкого трения Fтрен= b  bw0A cos(w0t +j), тогда среднее значение работы < Атрен > за единицу времени против этой силы равно: bw0A cos(w0t +j), тогда среднее значение работы < Атрен > за единицу времени против этой силы равно:
< Атрен > =  . .
Выразим cos2(w0t + j) через функцию двойного угла: cos2 a =  (1+cos2a) и подставим его в выражение для < Атрен >: (1+cos2a) и подставим его в выражение для < Атрен >:
< Атрен > =  = = 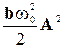 , (5-30) , (5-30)
поскольку значение второго интеграла в (5-30) равно нулю (среднее значение за период любой гармонической функции равно 0, т.к. эта функция половину периода положительна, а половину - отрицательна).
Очевидно, что за весь период Т, на преодоление силы трения будет затрачена энергия Wпотер = < Атрен > Т, и добротность колебательной системы может быть определена как:
 , (5-31) , (5-31)
где  . Из выражения (5-31) видно, что добротность системы определяется ее упругими, инерционными и диссипативными свойствами. Можно сказать также, что добротность - это число, показывающее, за сколько периодов колебаний вся энергия, запасенная в системе, будет превращена в работу против сил трения, т.е. в тепло. . Из выражения (5-31) видно, что добротность системы определяется ее упругими, инерционными и диссипативными свойствами. Можно сказать также, что добротность - это число, показывающее, за сколько периодов колебаний вся энергия, запасенная в системе, будет превращена в работу против сил трения, т.е. в тепло.
Как правило, добротность механических систем довольно высока. Здесь уместно вспомнить о звучании музыкальных инструментов: отдельная нота может звучать несколько секунд, хотя частота колебаний составляет несколько килогерц.
|