
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Реактивное движение. Уравнение движения тела переменной массы.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Движение некоторых тел сопровождается изменением их массы, например масса ракеты уменьшается за счет истечения газов, образующихся при сгорании топлива, и т. п. Выведем уравнение движения тела переменной массы на примере движения ракеты. Если в момент времени tмасса ракеты m, а ее скорость v, то по истечении времени dt ее масса уменьшится на dm и станет равной m - dm, а скорость станет равной
где
( Если на систему действуют внешние силы, то
где Если Таким образом, мы получили уравнение движения тела переменной массы
Это уравнение впервые было выведено И. В.Мещерским (1859—1935). Идея применения реактивной силы для создания летательных аппаратов высказывалась в 1881 г. Н. И. Кибальчичем (1854—1881). К.Э.Циолковский (1857— 1935) в 1903 г. опубликовал статью, где предложил теорию движения ракеты и основы теории жидкостного реактивного двигателя. Поэтому его считают основателем отечественной космонавтики. Применим уравнение (2-10) к движению ракеты, на которую не действуют никакие внешние силы. Полагая
Значение постоянной интегрирования С определим из начальных условий. Если в начальный момент времени скорость ракеты равна нулю, а ее стартовая масса то,
(2-11) называется формулой Циолковского. Из этой формулы следует, что: 1) чем больше конечная масса ракеты m, тем больше должна быть стартовая масса ракеты; 2) чем больше скорость истечения
Работа и мощность Пусть тело под действием постоянной силы совершило перемещение s (Рис.2.3). Перемещение тела обусловлено касательной составляющей силы Fcos Произведение движущей силы на перемещение называется работой:
При
при В случае переменной силы и криволинейного пути формулой (2-12) пользоваться нельзя. В этом случае, рассматривая элементарное перемещение
где Работа силы на участке траектории от точки 1 до точки 2 определяется интегрированием
Работа является скалярной величиной и измеряется в Джоулях.
Для того, чтобы знать как быстро совершается работа, вводят понятие мощности:
Если тело под действием постоянной силы движется с постоянной скоростью, то мощность можно выразить в виде
Мощность тоже скалярная величина. Единица мощности – ватт. 1Вт – мощность, при которой за 1 с совершается работа, равная 1 Дж.
2.8. Энергия. Закон сохранения энергии Энергия характеризует состояние системы, способность системы к совершению работы при переходе из одного состояния в другое. Изменение энергии выражается работой, которую может совершить система, переходя из одного состояния в другое, т.е.:
где Кинетическая энергия механической системы – это энергия механического движения этой системы. Определим эту энергию. Пусть тело под действием силы
Согласно второго закона Ньютона
Если учесть, что
Кинетическая энергия зависит только от скорости и массы тела. Потенциальная энергия – механическая энергия системы тел, определяемая их взаимным расположением и характером сил взаимодействия между ними. Силы, работа которых не зависит от формы пути, называются потенциальными, а поле этих сил – потенциальным. Тело, находясь в потенциальном поле, обладает потенциальной энергией. Работа, совершенная в этом поле равна приращению потенциальной энергии:
Потенциальная энергия тела массой m, поднятого на высоту h над поверхностью Земли, равна
Определим потенциальную энергию упругодеформированного тела. Элементарная работа при бесконечно малой деформации
Таким образом, Полная энергия системы складывается из всех присущих системе видов энергии. Закон сохранения и превращения энергии в изолированной системе: Полная энергия изолированной системы остается постоянной. При этом, будучи несозидаемой и неуничтожаемой, энергия может превращаться из одних видов другие. Закон сохранения и превращения энергии в неизолированной системе: Изменение энергии неизолированной системы равно работе, совершаемой системой:
Если работа совершается внутренними силами самой системы, то работа положительна и энергия системы убывает. Если же работа совершается внешними силами над системой, то работа отрицательно и энергия системы возрастает. Закон сохранения и превращения энергии раскрывает физический смысл понятий энергии и работы. Таким образом, энергия является количественной и качественной характеристикой движения материи, а работа – количественная характеристика превращения одних форм движения материи в другое. Лекция № 3 Динамика вращательного движения. Понятие абсолютно твердого тела. Поступательное и вращательное движение тела. Центр масс. Момент силы. Вращение твердого тела вокруг неподвижной оси, его момент инерции и кинетическая энергия. Момент импульса. Закон сохранения момента импульса. Второй закон динамики для вращательного движения.
|
||
|
Последнее изменение этой страницы: 2016-12-16; просмотров: 771; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.012 с.) |

 . Изменение импульса системы за отрезок времени dt
. Изменение импульса системы за отрезок времени dt
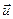 — скорость истечения газов относительно ракеты. Тогда
— скорость истечения газов относительно ракеты. Тогда
 — малый высшего порядка малости по сравнению с остальными).
— малый высшего порядка малости по сравнению с остальными). , поэтому
, поэтому ,
, , (2-9)
, (2-9) - реактивная сила.
- реактивная сила. , то ракета ускоряется, а если совпадает с
, то ракета ускоряется, а если совпадает с 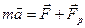 . (2-10)
. (2-10)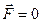 и считая, что скорость выбрасываемых газов относительно ракеты постоянна (ракета движется прямолинейно), получим
и считая, что скорость выбрасываемых газов относительно ракеты постоянна (ракета движется прямолинейно), получим

 .
. . Следовательно,
. Следовательно, . (2-11)
. (2-11) газов, тем больше может быть конечная масса при данной стартовой массе ракеты.
газов, тем больше может быть конечная масса при данной стартовой массе ракеты.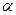 , которая называется движущей силой. Нормальная составляющая силы Fsin
, которая называется движущей силой. Нормальная составляющая силы Fsin  . (2-12)
. (2-12) работа положительна и сила вызывает перемещение тела;
работа положительна и сила вызывает перемещение тела;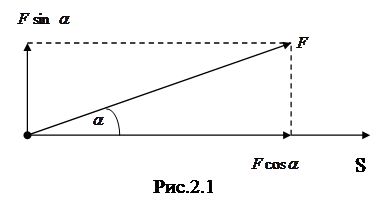
 работа отрицательна и сила препятствует движению тела; при
работа отрицательна и сила препятствует движению тела; при  сила не совершает работы по перемещению; при
сила не совершает работы по перемещению; при 
 , силу
, силу  можно считать постоянной и движение прямолинейным. Элементарной работой силы
можно считать постоянной и движение прямолинейным. Элементарной работой силы 
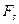 - проекция вектора
- проекция вектора  .
.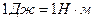 . 1Дж – работа, совершаемая силой 1 Н при перемещении тела на расстояние 1 м в направлении действия силы.
. 1Дж – работа, совершаемая силой 1 Н при перемещении тела на расстояние 1 м в направлении действия силы. .
. .
.

 ,
, и
и  - энергии системы в исходном и конечном состояниях.
- энергии системы в исходном и конечном состояниях. .
. Умножая обе части этого равенства на
Умножая обе части этого равенства на 
 , то
, то  .
.  .
. .
.
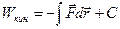 .
. .
.
 .
. .
. .
.


